PRECALC 101 FINAL EXAM SEM 1_6.1.3 Final Exam: Semester Exam (Teacher-Scored) Test Precalculus Honors Points Possible:100 Date: 03/11/2022. Score 100%

Document Content and Description Below

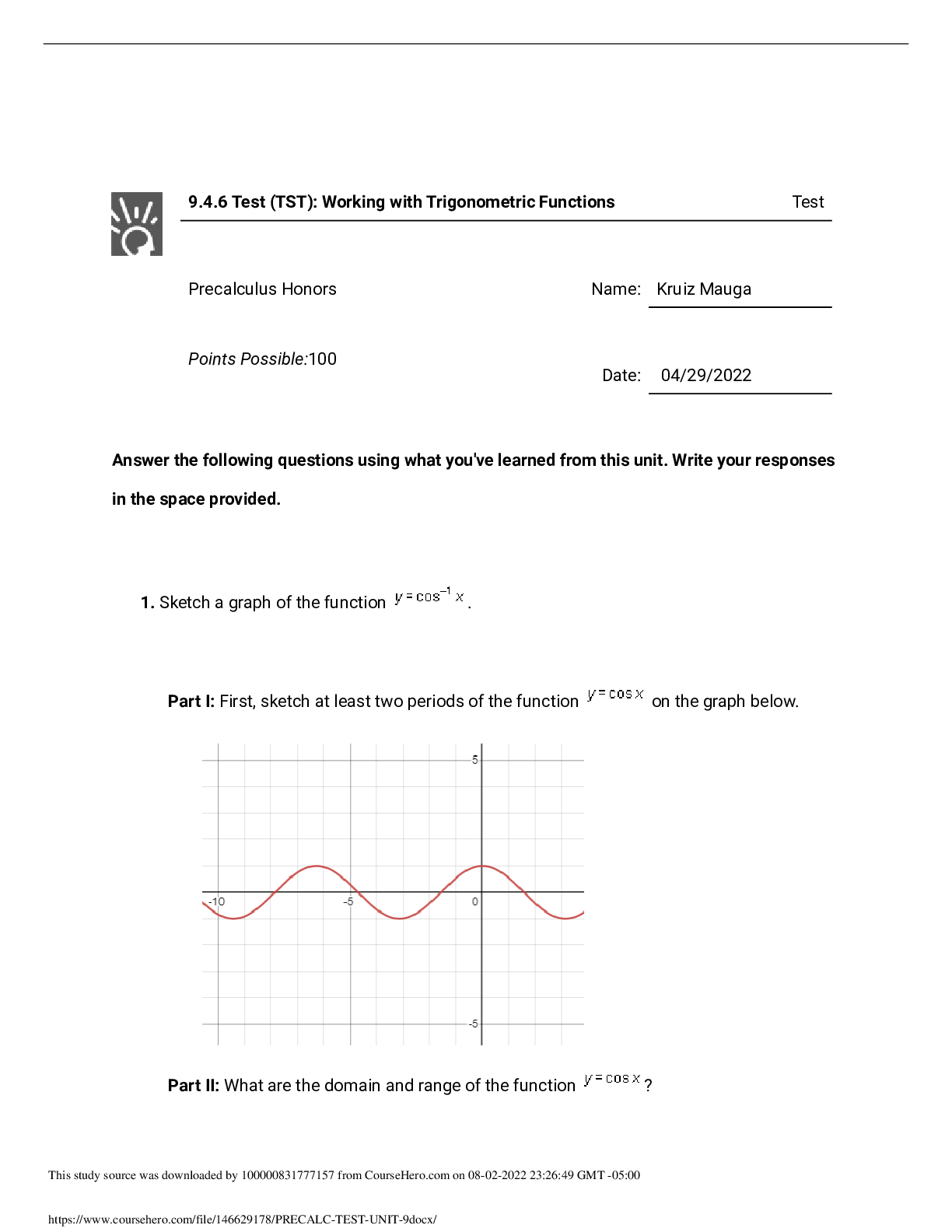
6.1.3 Final Exam: Semester Exam (Teacher-Scored) Test Precalculus Honors Points Possible:100 Date: 03/11/2022 Answer the following questions using what you've learned from this unit. Write your ... responses in the space provided. 1. You have relatives living in the United Kingdom and in France. Suppose that you have purchased a prepaid phone card with a value of $75. Calls to the United Kingdom cost 23¢ per minute, while calls to France cost 21¢ per minute. Part I: Write separate expressions for the total cost of calling to the United Kingdom, U(x), for a total of x minutes and for the total cost of calling to France, F(y), for a total of y minutes. (4 points) Part II: Write a linear inequality involving x and y to represent the number of minutes you can use to call the two countries and not exceed the value of your prepaid calling card. Part III: Graph the inequality you just wrote on the graph shown below. (2 points) Part IV: Suppose you anticipate needing to call the UK for a total of 250 minutes and France for 100 minutes. Will a $75 card cover the cost of this much calling? Explain your answer. (2 points) 78.5 dollars is less than 75 dollars, so NO, the card will not cover this much calling.2. Solve the following system of equations. Part I: Solve the system algebraically, using any method you like. Express your answer in the form (x,y). (4 points) Part II: Graph each of these lines on the graph shown below. (4 points)Part III: What are the coordinates of the point of intersection of the two lines on your graph? (2 points) 3. A local store owner pays her employees time-and-a-half for overtime. That means for every hour an employee works more than 40 hours per week, the store will pay 1.5 times the regular hourly wage of 14.50. Part I: Write a function, P(x), that defines the weekly pay for employees who work up to but not more than 40 hours in a week. (2 points) Part II: Suppose an employee works overtime (more than 40 hours per week). What is the hourly wage for the overtime hours? (1 point) Part III: Follow these steps to write a function, P(x), that defines the total weekly pay for employees who work more than 40 hours in a week. (4 points) a. How much does an employee make working the first 40 hours at $14.50 an hour? (1 point) 580 dollars. b. If an employee works x > 40 hours per week, write an expression for the overtime pay. (1 point)Hint: The employee works (x-40) overtime hours. overtime pay = (overtime hourly wage) • (number of overtime hours) c. Use your answer from parts (a) and (b) to write the function P(x), that defines the total weekly pay for employees who work more than 40 hours in a week. (2 points) Part IV: Use the functions from Part I and Part III to write the piecewise function for how much an employee will be paid if he or she were to work less than or equal to 40 hours, or more than 40 hours. (2 points) Part V: Use the function from Part III to determine how much an employee will be paid if he or she were to work 50 hours in a week. (1 point) 4. For the polynomial , answer the following questions: Part I: How many zeros does the function have over the set of complex numbers? (2 points)3 zeros Part II: What is the maximum number of local extrema (maxima or minima) the graph of the function can have? (2 points) 2 local extremas Part III: (4 points) a. What value does the function (y) approach as x approaches ? It will also approach infinity b. What value does the function (y) approach as x approaches - ? It will approach negative infinity Part IV: List the possible rational zeros of this function. (2 points) Part V: Factor this polynomial completely over the set of complex numbers. (6 points) 5. Graph .Part I: Which conic section does this equation represent? Explain your answer. (2 points) It is an ellipse because both y and x are squared, they have the same coefficients and signs, and it is what the graph shows. Part II: What are the coordinates of the four vertices and the two foci? (4 points) Four vertices= ( Part III: Graph this ellipse using the graph shown below. Clearly label the locations of the foci and the vertices. You do not need to label their coordinates. (4 points) foci vertices6. Graph . Part I: What kind of conic section does this equation represent? Explain your answer. (2 points) This is a hyperbola because it has all of the requirements of an ellipse except the sign are different on x and y. Part II: Find the coordinates of the two vertices and the two foci. (4 points) Part III: Write the equations of the two asymptotes. (2 points) Part IV: Graph this hyperbola using the graph shown below. Clearly label the locations of the foci and the vertices. You do not need to label their coordinates. (4 points)7. Consider the function . Part I: What is the equation of this function's vertical asymptote? (2 points) Part II: What is the equation of this function's additional asymptote? (4 points) Part III: Sketch the graph of this function on the graph below. (4 points) foci vertices8. Use synthetic division to find the quotient and the remainder for the problem . Part I: Set up the synthetic division problem by transferring the divisor and the coefficients from the dividend into a division table. (4 points)Part II: Carry out the division and write your answer as . (4 points) Part III: Is a factor of the polynomial ? Explain your answer. (2 points) No because the remainder is not zero, the remainder is 5. 9. The Richter scale is used to measure the magnitude of an earthquake. The magnitude, R, is given by the equation , where E is the energy (measured in kilowatt-hours) released by the earthquake. Determine the amount of energy released by an earthquake of magnitude 7.5. Part I: Simplify the problem so that it is written in the form (6 points)10^(6.05/0.65)/0.39=E Part II: Solve the problem for E, the energy released by the earthquake.(6 points) [Show More]

Last updated: 1 year ago

Preview 1 out of 13 pages