Georgia Institute Of TechnologyISYE 6644Homework 9 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science

Document Content and Description Below

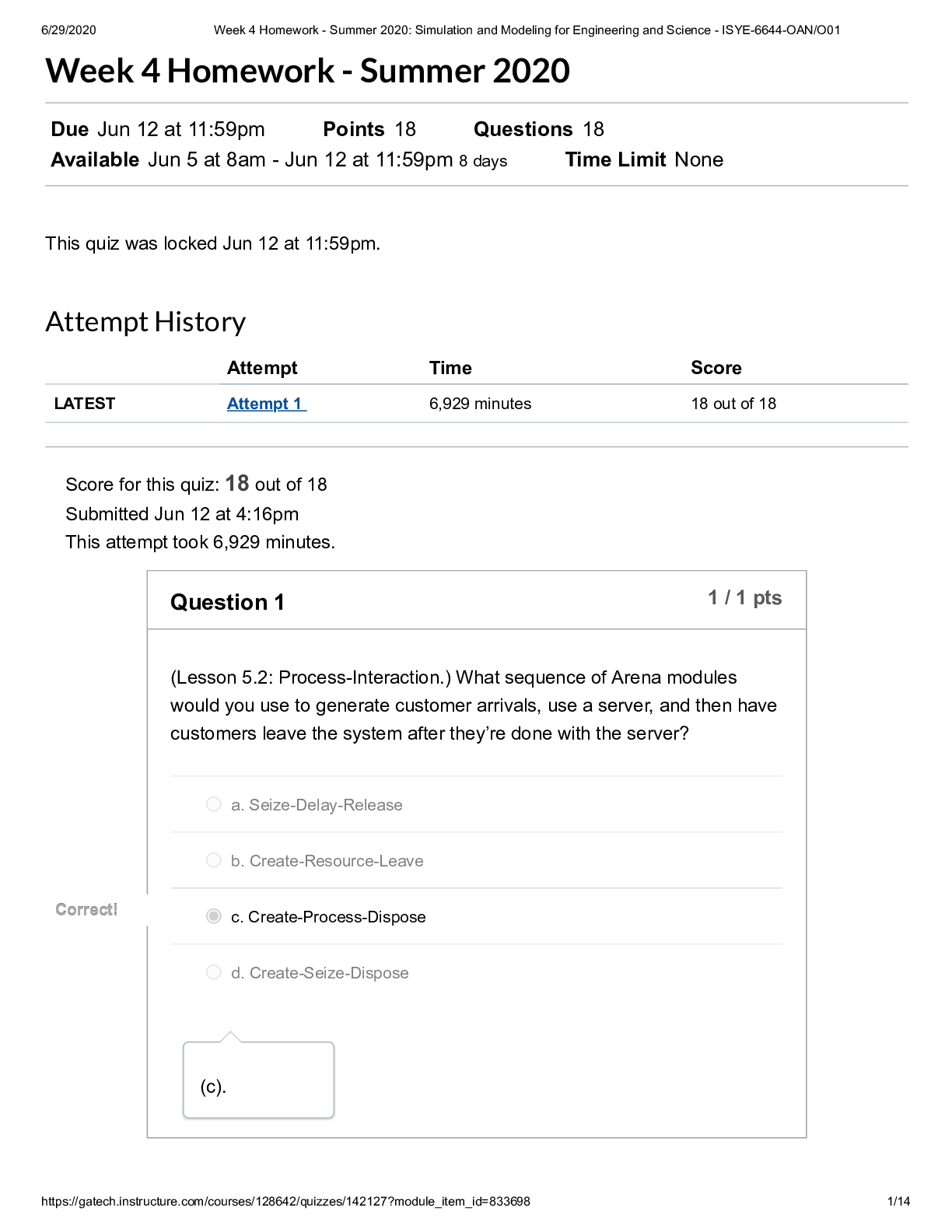
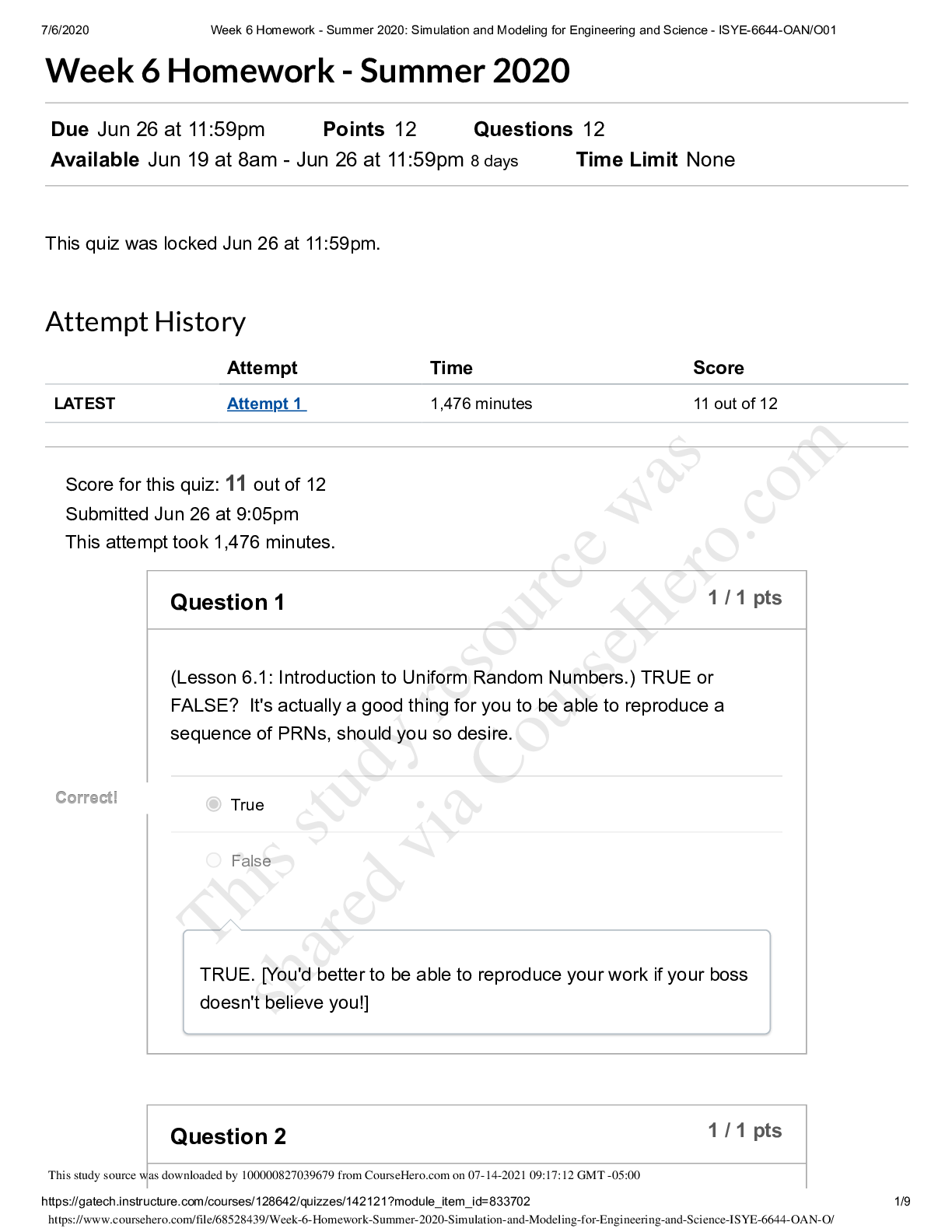
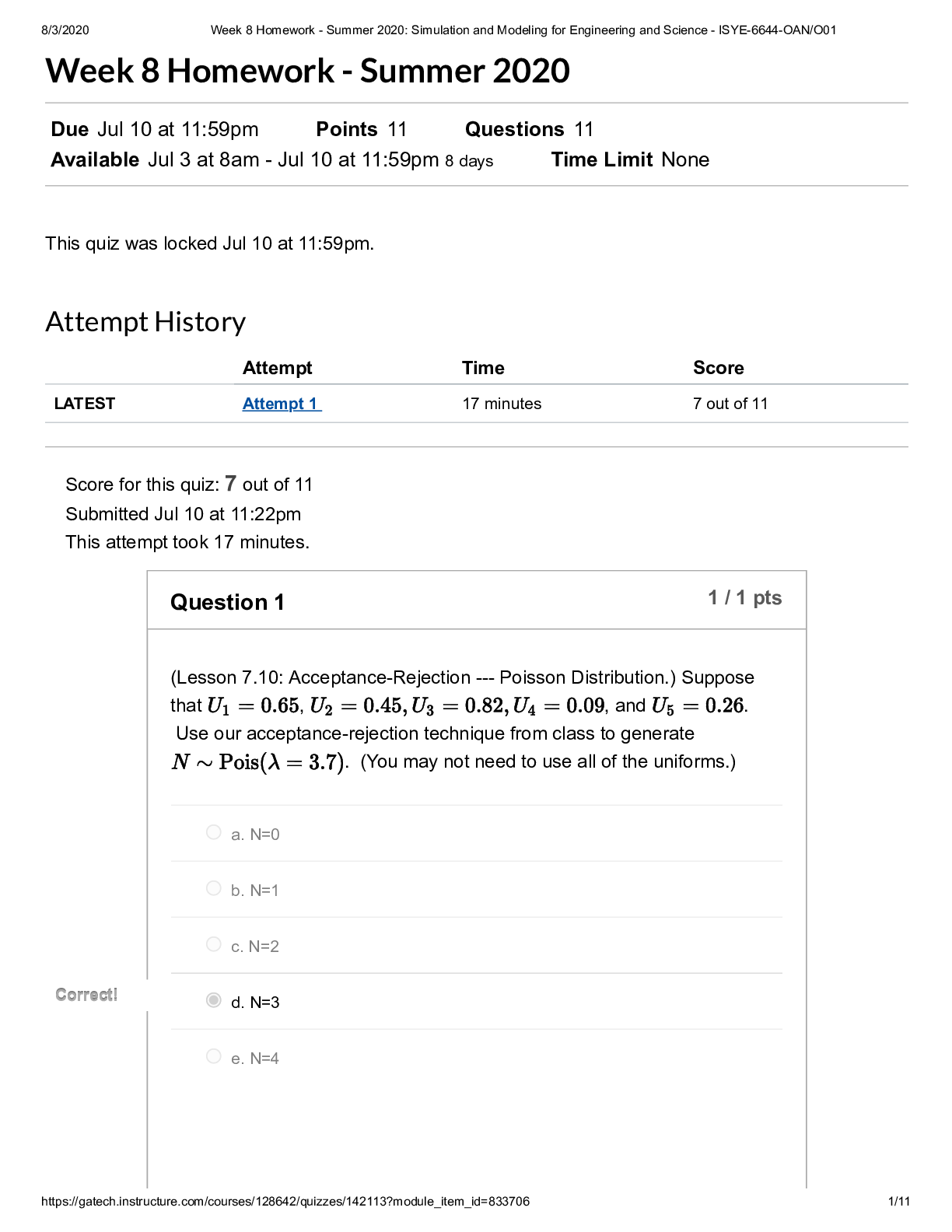
8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 1/14... Week 9 Homework - Summer 2020 Due Jul 17 at 11:59pm Points 17 Questions 17 Available Jul 10 at 8am - Jul 17 at 11:59pm 8 days Time Limit None This quiz was locked Jul 17 at 11:59pm. Attempt History Attempt Time Score LATEST Attempt 1 223 minutes 15 out of 17 Score for this quiz: 15 out of 17 Submitted Jul 17 at 10:15pm This attempt took 223 minutes. Question 1 1 / 1 pts (Lesson 8.1: Introduction to Input Modeling.) It's GIGO time! Let's consider an queueing system with Exp( ) interarrivals and Exp( ) FIFO services at a single server. You may recall from some class (either this one or stochastic processes) that the steady-state expected cycle time (i.e., the time that the customer is in the system, including wait + service) is . If you were to try this out in Arena, let's say with interarrivals and services (note the notation change between my usual "Exp" and Arena's ), then we'd get . Go ahead, see for yourself in Arena, but make sure that you run the system for 100,000 or so customers so that you can be sure that you're in steady-state! Finally, here's the GIGO question, which will show what can happen when you mis-model a component of your process: What is the (approximate) steady-state expected cycle time if you have i.i.d. interarrivals instead of interarrivals? Note that both interarrival distributions have the same mean (10), but that doesn't8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 2/14 necessarily imply that they'll have the same expected cycle times. Hint: You may want to use Arena as described above. a. about 1 b. about 10 Correct! Correct! c. about 23 d. about 40 e. about 62 (c). The case has waaaay smaller tails than the , so it's reasonable to assume that the cycle times will tend to be lower for the case. In fact, after 100,000 customers in Arena, I got an average time of 23.5. Thus, (c) is the right answer. Question 2 0 / 1 pts (Lesson 8.2: Identifying Distributions.) Let's play Name That Distribution! The number of times a "3" comes up in 10 dice tosses. ou Answered ou Answered a. Bernoulli orrect Answer orrect Answer b. Binomial c. Geometric d. Negative Binomial e. Pareto8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 3/14 (b). Question 3 1 / 1 pts (Lesson 8.2: Identifying Distributions.) Name That Distribution! The number of dice tosses until a 3 comes up. a. Bernoulli b. Binomial Correct! Correct! c. Geometric d. Negative Binomial e. Pareto (c). Question 4 1 / 1 pts (Lesson 8.2: Identifying Distributions.) Name That Distribution! The number of dice tosses until a 3 comes up for the 4th time. a. Bernoulli b. Binomial8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 4/14 c. Geometric Correct! Correct! d. Negative Binomial e. Pareto (d). Question 5 1 / 1 pts (Lesson 8.2: Identifying Distributions.) Name That Distribution! IQs a. Uniform Correct! Correct! b. Normal c. Exponential d. Weibull e. Pareto (b). Question 6 1 / 1 pts (Lesson 8.2: Identifying Distributions.) Name That Distribution!8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 5/14 Cases in which you have limited information, e.g., you only know the min, max, and "most likely" values that a random variable can take. a. Bernoulli b. Poisson Correct! Correct! c. Triangular d. Weibull e. Pareto (c). Question 7 1 / 1 pts (Lesson 8.3: Unbiased Point Estimation.) Find the sample variance of a. 0 b. 1 c. 4 Correct! Correct! d. 14/3 e. 68/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 6/14 So the answer is (d). Question 8 1 / 1 pts (Lesson 8.3: Unbiased Point Estimation.) If are i.i.d. Pois(6), what is the expected value of the sample variance ? a. 1/6 b. 1/36 Correct! Correct! c. 6 d. 36 e. 60 is always unbiased for the variance of . Thus, we have . So the answer is (c). Question 9 1 / 1 pts (Lesson 8.4: Mean Squared Error.) Suppose that estimator A has bias = 3 and variance = 12, while estimator B has bias -2 and variance = 14. Which estimator (A or B) has the lower mean squared error?8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 7/14 a. A Correct! Correct! b. B MSE = Bias + Var, so Thus, B has lower MSE. Question 10 1 / 1 pts (Lessons 8.5 and 8.6: Maximum Likelihood Estimators.) If , , and are i.i.d. realizations from a Nor( ) distribution, what is the value of the maximum likelihood estimate for the variance ? a. 0 b. 1 Correct! Correct! c. 8/3 d. 4 e. None of the above We know from a class example that Thus, the answer is (c).8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 8/14 Question 11 1 / 1 pts (Lessons 8.5 and 8.6: Maximum Likelihood Estimators.) Suppose we observe the Pois realizations and . What is the maximum likelihood estimate of ? a. 0 Correct! Correct! b. 5 c. 25 d. 1/5 e. 1/25 I don't remember if we derived the MLE of in class or not, but here's how anyway. The likelihood function is Thus, This implies that Setting the derivative to 0 and solving yields . Duh! What a surprise! So the answer is (b).8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 9/14 Question 12 0 / 1 pts (Lesson 8.7: Invariance Property of MLEs) Suppose that we have a number of observations from a Pois distribution, and it turns out that the MLE for is . What's the maximum likelihood estimate of ? orrect Answer orrect Answer a. 0.1404 ou Answered ou Answered b. 5 c. 25 d. 1/5 e. 1/25 By invariance, so that we have Thus, the answer is (a). Question 13 1 / 1 pts (Lesson 8.8: Method of Moments.) BONUS: Suppose that we observe , , and . What's the method of moments estimate of ?8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 10/14 a. 5 b. 25 Correct! Correct! c. 35.7 d. 1/5 e. 1/25 The MOM estimator for is . Thus, the answer is (c). Question 14 1 / 1 pts (Lesson 8.9: Goodness-of-Fit Tests.) Suppose we're conducting a goodness-of-fit test with Type I error rate to determine whether or not 100 i.i.d. observations are from a lognormal distribution with unknown parameters . If we divide the observations into 5 equal-probability intervals and we observe a g-o-f statistic of , will we ACCEPT or REJECT the null hypothesis of lognormality? Accept Correct! Correct! Reject8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 11/14 Note that the test has degrees of freedom. Then so we REJECT even though we're being conservative with such a small ! Question 15 1 / 1 pts (Lessons 8.10 and 8.11: Goodness-of-Fit Test.) This problem has a really long description, but the question itself will be very short! Be patient! The number of defects in printed circuit boards is hypothesized to follow a Geometric( ) distribution. A random sample of printed boards has been collected, and the number of defects observed. Here are the results. It turns out that the MLE of for the Geom( ) is . (See the following proof if you don't believe me!) Proof: The likelihood function is Thus, and so,8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 12/14 Solving for gives the MLE . So in this particular case, we have: and thus Anyhow, we are interested in performing a goodness-of-fit test to test the Geometric hypothesis. To this end, let's get the test statistic, ? To do so, let's make a little table, assuming that is correct. Note that the expected number of observations having a certain value is . Also note that I've combined the entries in the last row ( ) so the probabilities add up to one. Technically speaking, we really ought to combine the last two cells, since . Let's do so to get the following new-and-improved table. Thus, the test statistic is8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 13/14 Now, let's use our old friend in our test. Let denote the number of cells (that we ultimately ended up with) and let denote the number of parameters we had to estimate. Then we compare against . So after all this time, here's my question: Do we ACCEPT or REJECT the Geometric hypothesis? a. Accept Correct! Correct! b. Reject Since , we REJECT. That wasn't so bad, was it? Question 16 1 / 1 pts (Lesson 8.12: Kolmogorov--Smirnov Test.) Consider the PRN's . Use Kolmogorov-Smirnov with to test to see if these numbers are indeed uniform. Do we ACCEPT or REJECT uniformity? Correct! Correct! a. Accept b. Reject8/3/2020 Week 9 Homework - Summer 2020: Simulation and Modeling for Engineering and Science - ISYE-6644-OAN/O01 https://gatech.instructure.com/courses/128642/quizzes/142131?module_item_id=833708 14/14 Need to make a little table, where the denote the ordered PRN's. Thus, , and , and so finally the K-S test stat is . The necessary quantile is . Since , we ACCEPT uniformity (though it's kind of a joke since it's only based on 3 observations) Question 17 1 / 1 pts (Lesson 8.14: Arena Input Analyzer.) You don't have to turn anything in for this, but I'd simply like you to play around with the Arena Input Analyzer. So, did you look at the Input Analyzer? (You should answer YES.) Correct! Correct! a. Yes b. No Quiz Score: 15 out of 17 [Show More]

Last updated: 1 year ago

Preview 1 out of 14 pages