MATH 225N Week 4 Probability Questions and answers_2021_Already Graded A. LATEST FOR 2021/2022

Document Content and Description Below

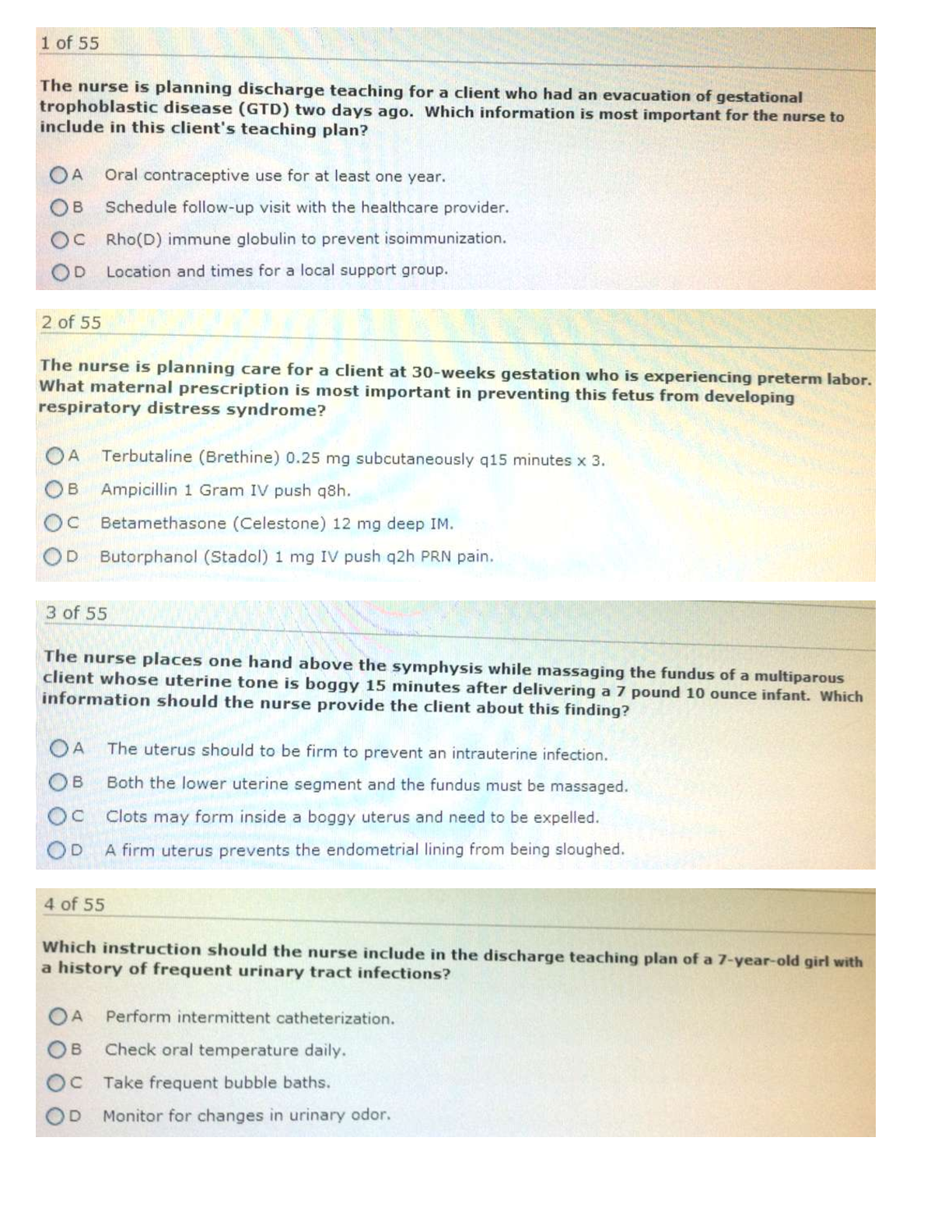
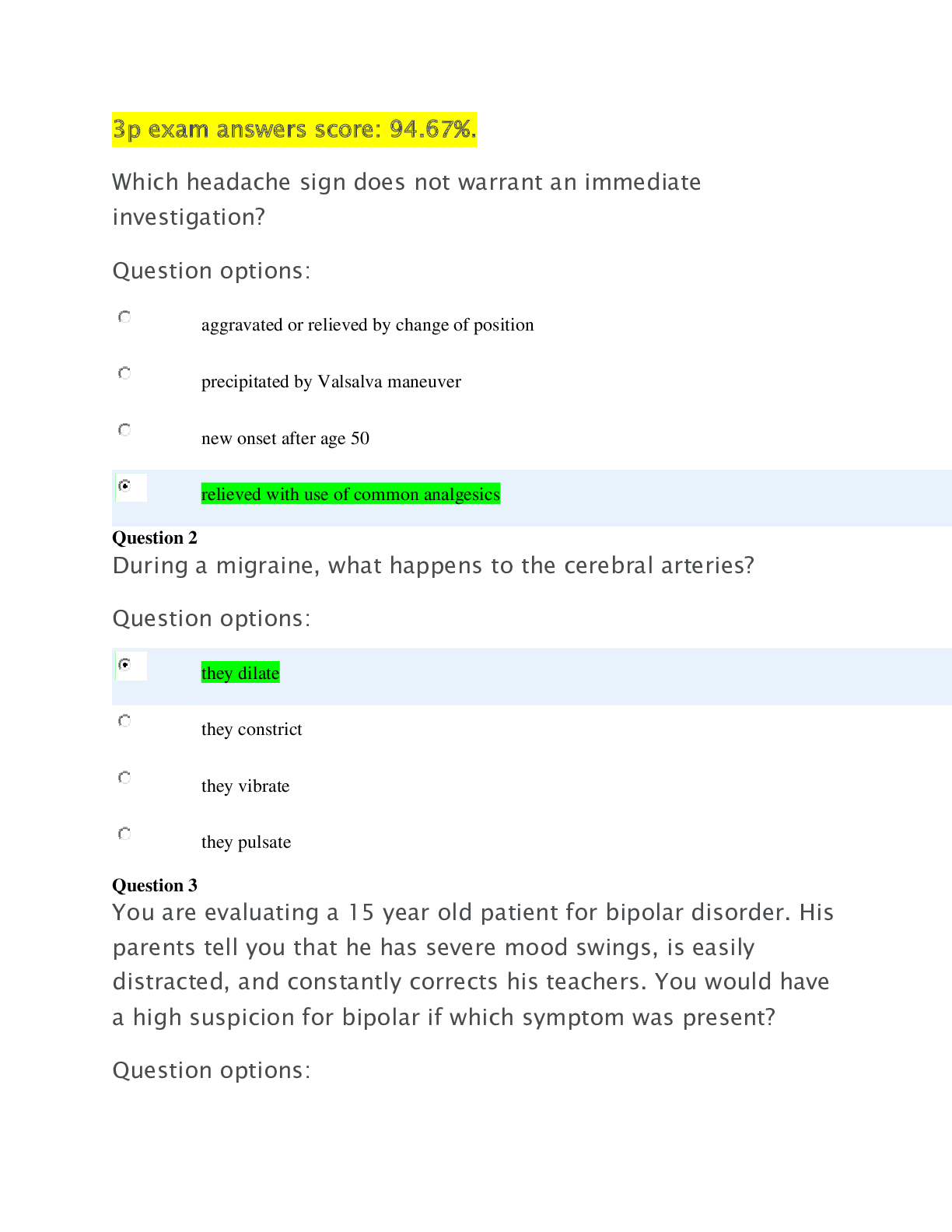
1. Which of the pairs of events below is dependent? Select the correct answer below: drawing a 7 and then drawing another 7 with replacement from a standard deck of cards rolling a 1 and then rolli ng... a 6 with a standard die rolling a 3 and then rolling a 4 with a standard die drawing a heart and then drawing a spade without replacement from a standard deck of cards 2. Identify the option below that represents dependent events. Select the correct answer below: drawing a face card and then drawing a 3 without replacement from a standard deck of cards rolling a sum of 6 from the first two rolls of a standard die and a sum of 4 from the second two rolls drawing a 2 and drawing a 4 with replacement from a standard deck of cards drawing a heart and drawing another heart with replacement from a standard deck of cards 3. Which of the following shows mutually exclusive events? Select the correct answer below: rolling a sum of 9 from two rolls of a standard die and rolling 2 for the first roll drawing a red card and then drawing a black card with replacement from a standard deck of cards drawing a jack and then drawing a 7 without replacement from a standard deck of cards drawing a 7 and then drawing another 7 with replacement from a standard deck of cards 4. Which of the pairs of events below is mutually exclusive? Select the correct answer below: drawing an ace of spades and then drawing another ace of spades without replacement from a standard deck of cards drawing a 2 and drawing a 4 with replacement from a standard deck of cards drawing a heart and then drawing a spade without replacement from a standard deck of cards drawing a jack and then drawing a 7 without replacement from a standard deck of cards(Mutually exclusive events are events that cannot occur together. In this case, drawing an ace of spades and then drawing another ace of spades without replacement from a standard deck of cards are two events that cannot possibly occur together.) 5. A deck of cards contains RED cards numbered 1,2,3,4,5,6, BLUE cards numbered 1,2,3,4,5, and GREEN cards numbered 1,2,3,4. If a single card is picked at random, what is the probability that the card has an ODD number? Select the correct answer below: 10/15 8/15 14/15 6/15 (By counting, we can see that there are 8 odd cards, and a total of 15 cards in the deck. So the probability is 8/15). 6. Hector is a baseball fan but wants to watch something different. There are 5 basketball games, 2 football games, and 4hockey games that he can choose to watch. If Hector randomly chooses a game, what is the probability that it is a basketball game? Give your answer as a fraction. Provide your answer below: 5/11 7. There are 26 cards in a hat, each of them containing a different letter of the alphabet. If one card is chosen at random, what is the probability that it is not between the letters L and P, inclusive? Provide your answer below: 21/26 8. A spinner contains the numbers 1 through 80. What is the probability that the spinner will land on a number that is not a multiple of 12? Give your answer in fraction form. Provide your answer below: 74/80 9. An art collector wants to purchase a new piece of art. She is interested in 5 paintings, 6 vases, and 2 statues. If she chooses the piece at random, what is the probability that she selects a painting?Give your answer as a fraction. Provide your answer below: 5/13 10.Boris is taking a quiz for an online class. For the quiz, the system randomly assigns 2 highdifficulty questions, 7 moderate-difficulty questions, and 6 low-difficulty questions. What is the probability that Boris is assigned a moderate-difficulty question first? Give your answer as a fraction. Provide your answer below: 7/15 11.A spinner contains the numbers 1 through 40. What is the probability that the spinner will land on a number that is not a multiple of 6? Give your answer as a fraction. Provide your answer below: 34/40 12.A spinner contains the numbers 1 through 50. What is the probability that the spinner will land on a number that is not a multiple of 4? Provide your answer below: 38/50 13.Identify the parameters p and n in the following binomial distribution scenario. The probability of winning an arcade game is 0.718 and the probability of losing is 0.282. If you play the arcade game 20 times, we want to know the probability of winning more than 15 times. (Consider winning as a success in the binomial distribution.) p=0.282, n=20 p=0.718, n=15 p=0.718, n=20 p=0.282, n=15 (The parameters p and n represent the probability of success on any given trial and the total number of trials, respectively. In this case, success is winning a game, so p=0.718. The total number of trials, or games, is n=20) 14.A weighted coin has a 0.55 probability of landing on heads. If you toss the coin 14 times, what is the probability of getting heads exactly 9 times? (Round your answer to 3 decimal places if necessary.)Provide your answer below: 0.170 (This probability can be found using the binomial distribution with success probability p=0.55 and 14 trials. To find the probability that exactly 9 of the tosses are heads, use a calculator or computer: P(X=9)=binompdf(14,0.55,9)≈0.170. 15. Identify the parameter p in the following binomial distribution scenario. The probability of buying a movie ticket with a popcorn coupon is 0.546 and without a popcorn coupon is 0.454. If you buy 27 movie tickets, we want to know the probability that exactly 15 of the tickets have popcorn coupons. (Consider tickets with popcorn coupons as successes in the binomial distribution.) Select the correct answer below: 0.152 0.454 0.546 0.848 16.A softball pitcher has a 0.64 probability of throwing a strike for each pitch. If the softball pitcher throws 20 pitches, what is the probability that exactly 13 of them are strikes?  Round your answer to three decimal places. 0.184 This probability can be found using the binomial distribution with success probability p=0.64 and 20 trials. To find the probability that exactly 13 of the pitches are strikes, use a calculator or computer: P(X=13)=binompdf(20,0.64,13)=0.184. 17.Identify the parameter n in the following binomial distribution scenario. A basketball player has a 0.429 probability of making a free throw and a 0.571 probability of missing. If the player shoots 20 free throws, we want to know the probability that he makes no more than 12 of them. (Consider made free throws as successes in the binomial distribution.) Select the correct answer below: 8 12 20 3218. Give the numerical value of the parameter p in the following binomial distribution scenario. A softball pitcher has a 0.675 probability of throwing a strike for each pitch and a 0.325 probability of throwing a ball. If the softball pitcher throws 29 pitches, we want to know the probability that exactly 19 of them are strikes. Consider strikes as successes in the binomial distribution. Do not include p= in your answer. Provide your answer below: 0.675 (The parameters p and n represent the probability of success on any given trial and the total number of trials, respectively. In this case, success is a strike, so p=0.675) 19.Identify the parameters p and n in the following binomial distribution scenario. Jack, a bowler, has a 0.38 probability of throwing a strike and a 0.62 probability of not throwing a strike. Jack bowls 20times (Consider that throwing a strike is a success.) Select the correct answer below: p=0.38,n=0.62 p=0.38,n=10 p=0.38,n=20 p=0.62,n=10 p=0.62,n=20 (In a binomial distribution, there are only two possible outcomes. p denotes the probability of the event or trial resulting in a success. In this scenario, it would be the probability of Jack bowling a strike, which is 0.38. The total number of repeated and identical events or trials is denoted by n. In this scenario, Jack bowls a total of 20 times, so n=20). 20.The Stomping Elephants volleyball team plays 30 matches in a week-long tournament. On average, they win 4 out of every 6matches. What is the mean for the number of matches that th [Show More]

Last updated: 1 year ago

Preview 1 out of 27 pages