University of Maryland STAT 200 STAT 200 - Homework 6 Solutions

Document Content and Description Below

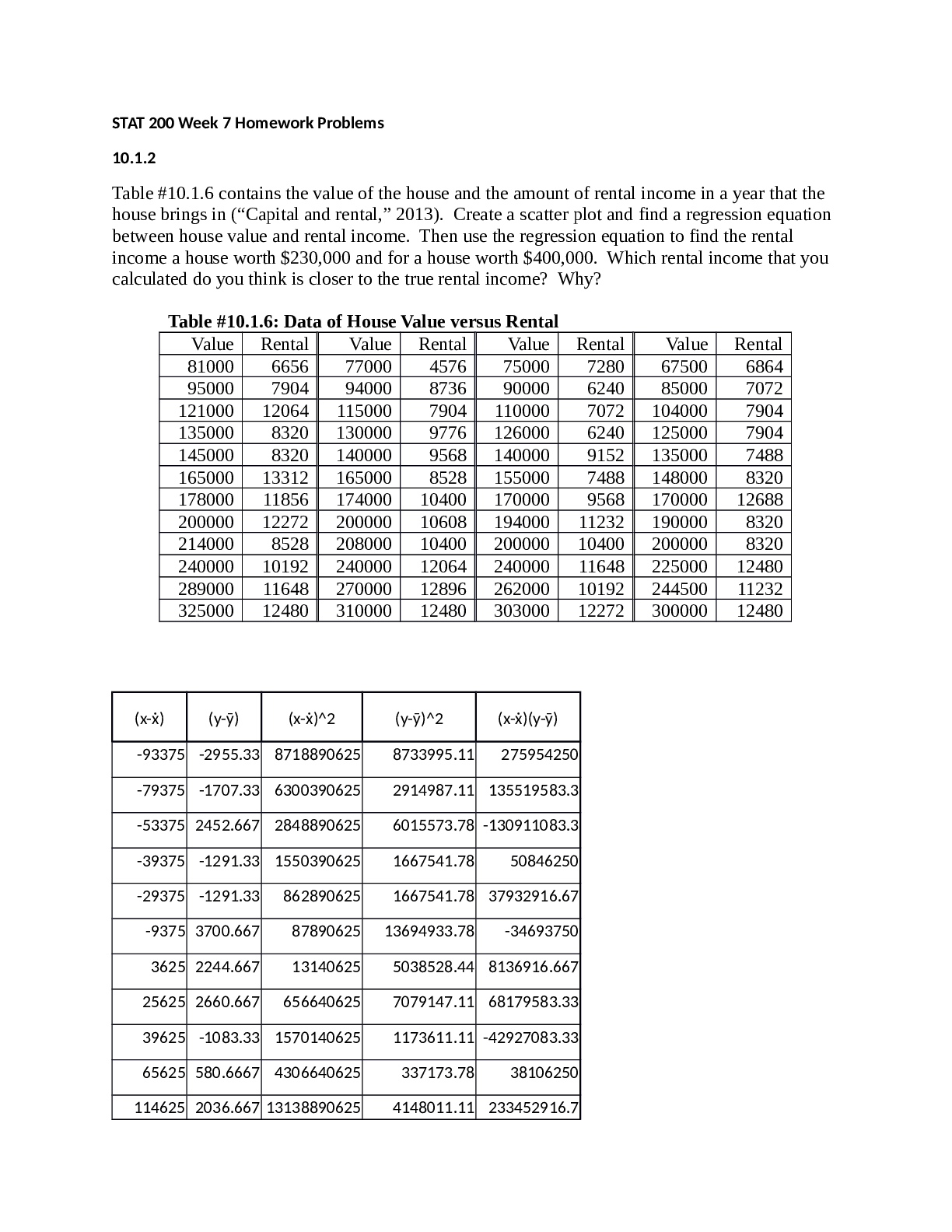
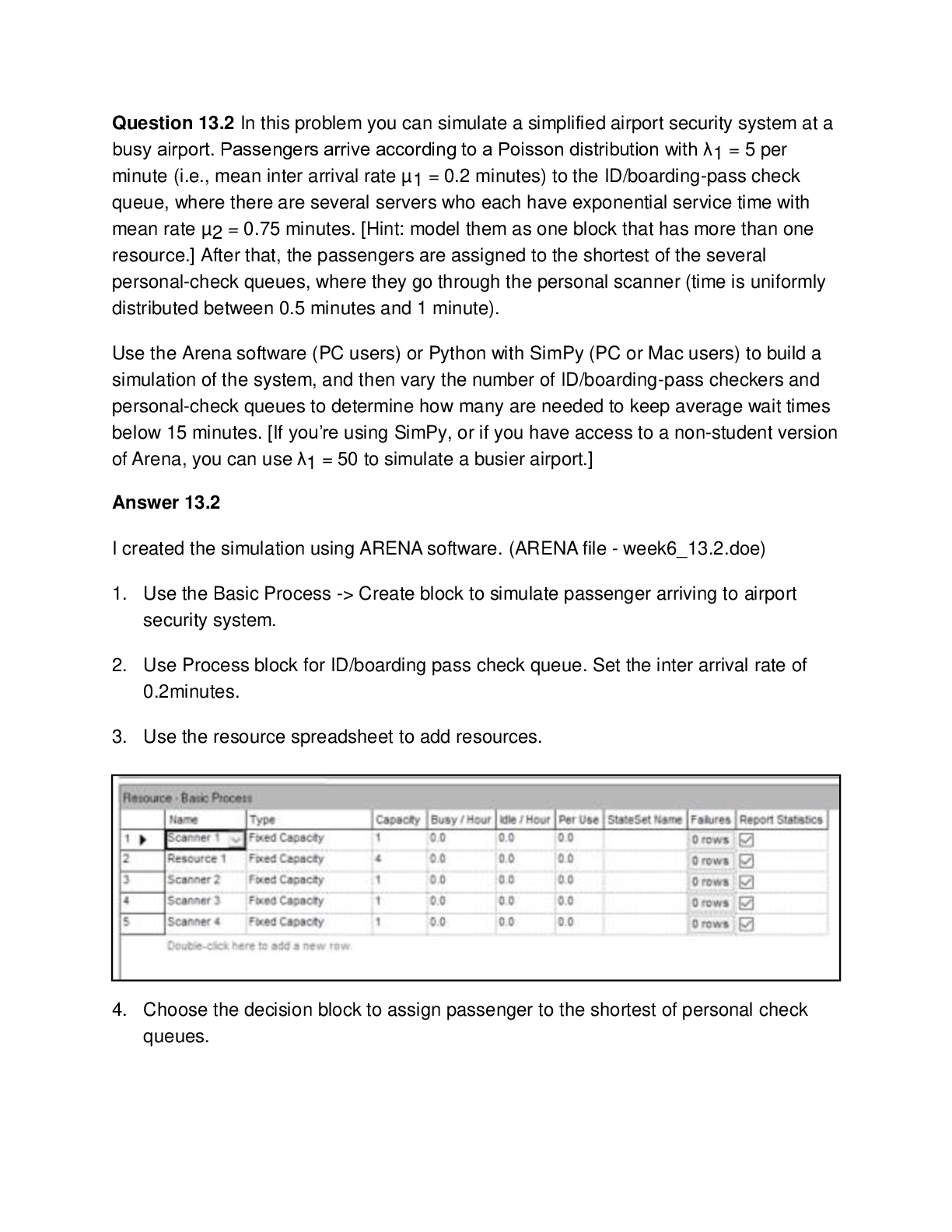
STAT 200: Introduction to Statistics Homework #6 1. (3 points): Many high school students take the AP tests in different subject areas. In 2007, of the 144,796 students who took the biology exam 84... ,199 of them were female. In that same year, of the 211,693 students who took the calculus AB exam 102,598 of them were female ("AP exam scores," 2013). Estimate the difference in the proportion of female students taking the biology exam and female students taking the calculus AB exam using a 90% confidence level. Interpret the results. First, we should start off by writing down what we know (always a good place to start). If you write down what you know and what you are trying to solve (purpose of analysis), you can usually determine what method you need to use to solve the problem. n1 = 144,796 n2 = 211,693 x1 = 84,199 x2 = 102,598 C = 1 - α = 1 - 0.9 = 0.1 (remember, the critical region refers to the area in the tail(s), and the confidence interval % refers to the area in the middle) Purpose of Analysis: For this problem, we are to estimate a 90% confidence interval on the difference in proportion of female students taking the biology and calculus AB exam. This difference is given by: p1 – p2 Thus, are computing a confidence interval for the difference between two population proportions. We need to compute the margin of error and add/subtract it from the difference in the sample proportions; we can follow the example on page 267 in the Kozak textbook. i.) State the random variable and the parameters in words. x1 = number of female students taking the biology exam x2 = number of female students taking the calculus AB exam p1 = proportion of female students taking the biology exam p2 = proportion of female students taking the calculus AB exam ii.) State and check the assumptions for confidence interval a.) A simple random sample of 1447,96 students taking the biology exam is taken. A simple random sample of 211,693 students taking the calculus AB exam is taken. Both samples were collected from all students for each exam during a particular year. This isn’t really a sample unless the year that was chosen at random, so this assumption may not have been met. b.) The samples are independent since different tests. c.) The assumptions for the binomial distribution are satisfied in both populations, since there are only two responses (female = success, male = failure), there are a fixed number of trials, the probability of a success is the same, and the trials are independent. [Show More]

Last updated: 1 year ago

Preview 1 out of 32 pages