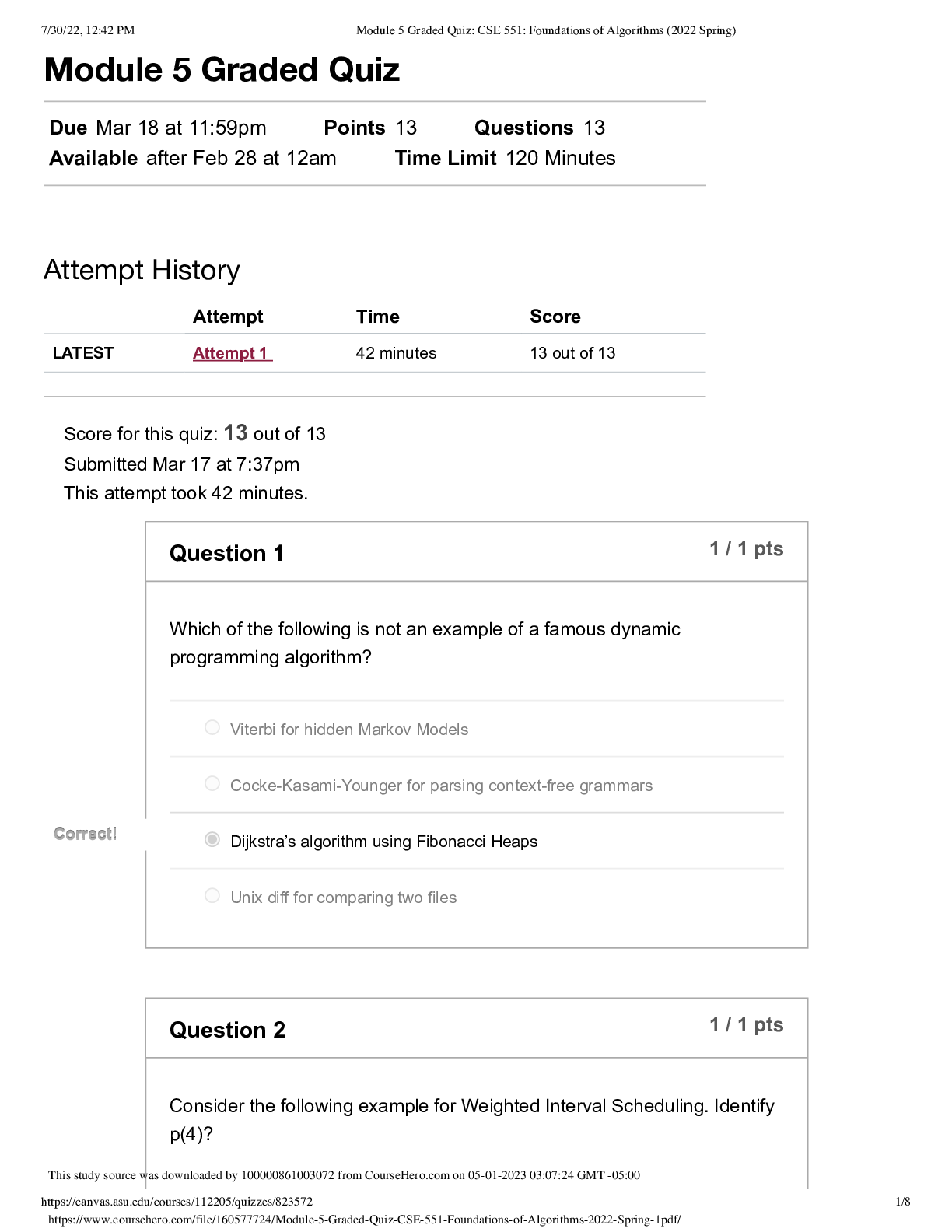
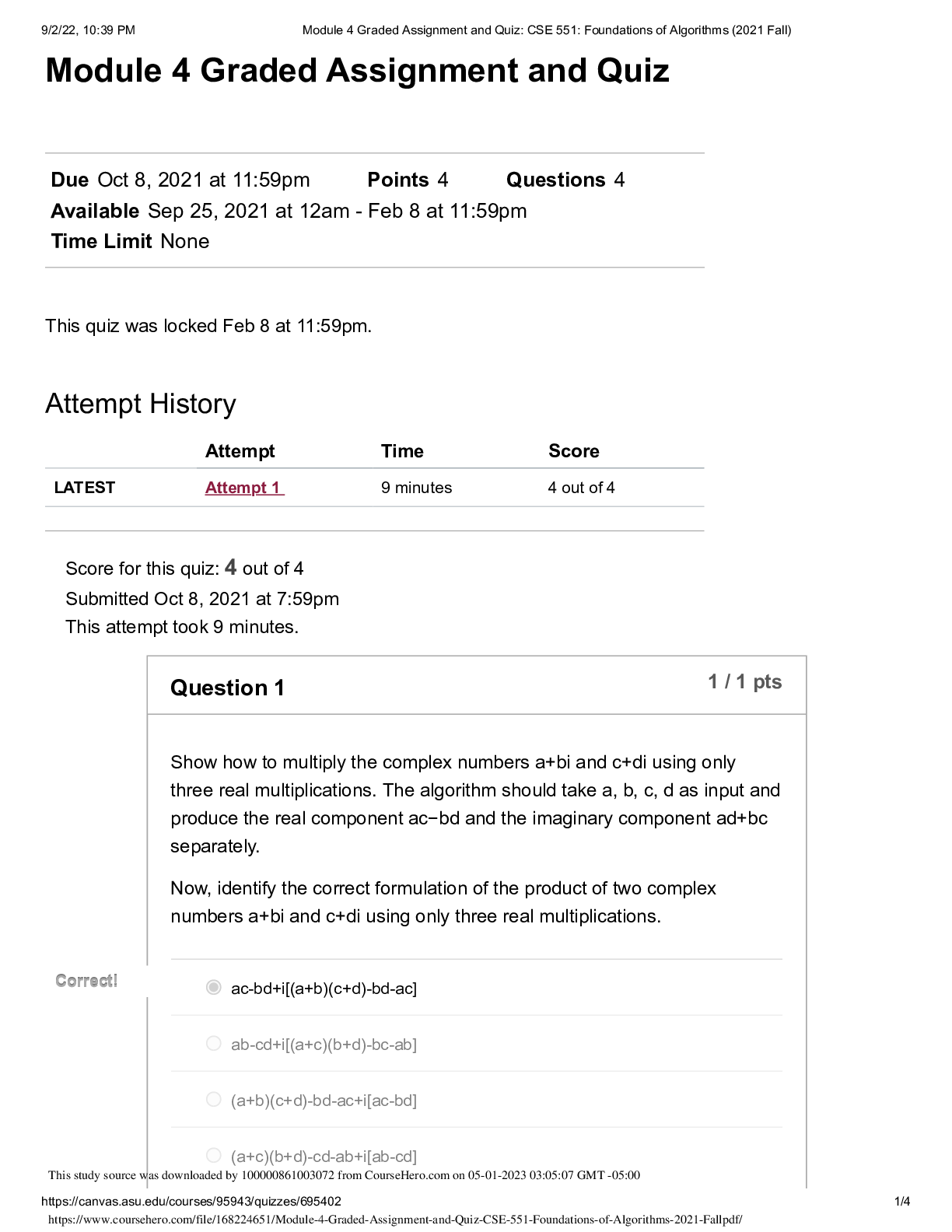
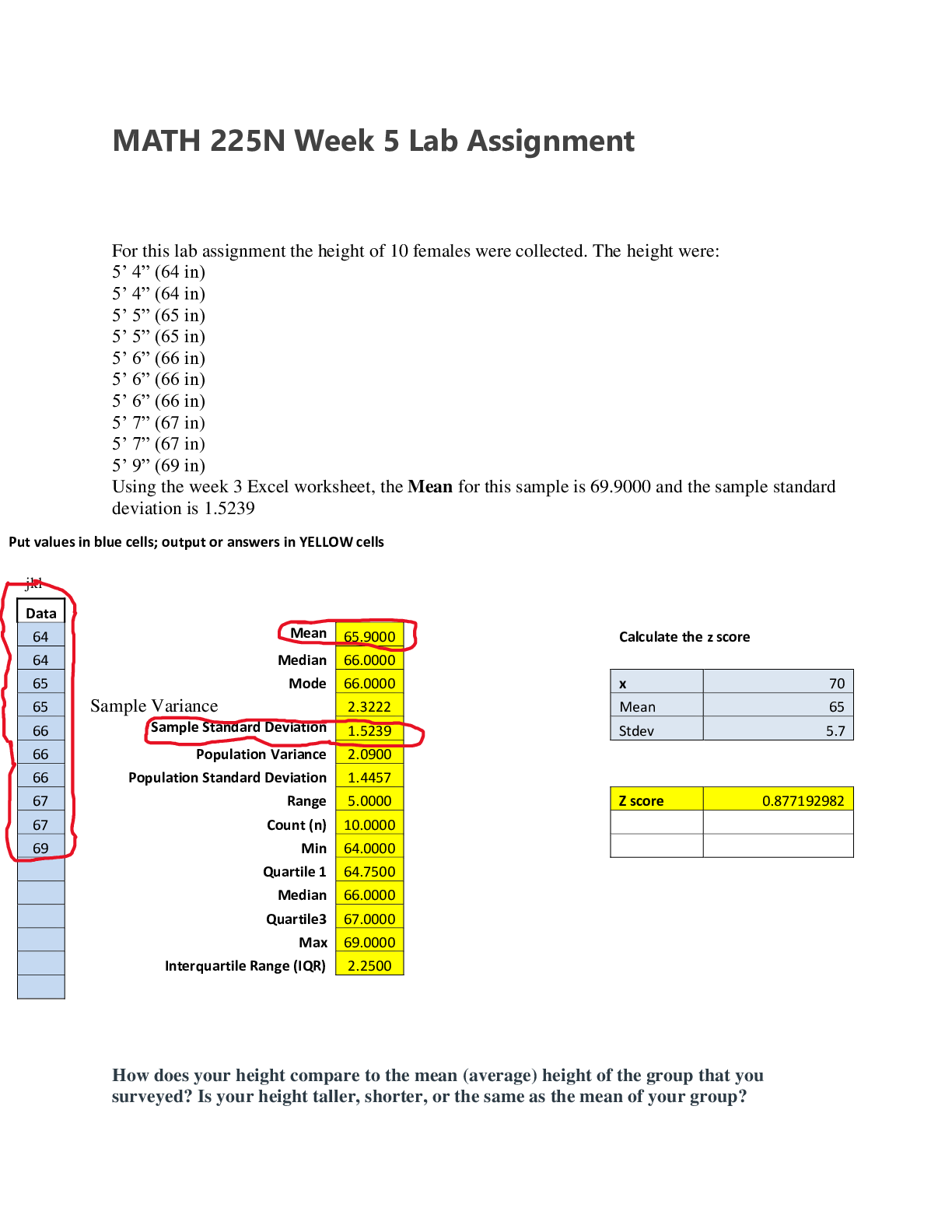
CS 70 Discrete Mathematics and Probability Theory -University of California, Berkeley. Summer 2020 HOMEWORK 6. Complete Q&A.

Document Content and Description Below

CS 70 Discrete Mathematics and Probability Theory Summer 2020 Course Notes HW 6 1 Unreliable Servers In a single cluster of a Google competitor, there are a huge number of servers n, each with a un... iform and independent probability of going down in a given day. On average, 4 servers go down in the cluster per day. As each cluster is responsible for a huge amount of internet traffic, it is fair to assume that n is a very large number. Recall that as n ! ¥, a Binom(n;l=n) distribution will tend towards a Poisson(l) distribution. (a) What is an appropriate distribution to model the number of servers that crash on any given day for a certain cluster? (b) Compute the expected value and variance of the number of crashed servers on a given day for a certain cluster. (c) Compute the probability that fewer than 3 servers crashed on a given day for a certain cluster. (d) Compute the probability at least 3 servers crashed on a given day for a certain cluster. Solution: CS 70, Summer 2020, HW 6 1 2 Class Enrollment Lydia has just started her CalCentral enrollment appointment. She needs to register for a marine science class and CS 70. There are no waitlists, and she can attempt to enroll once per day in either class or both. The CalCentral enrollment system is strange and picky, so the probability of enrolling successfully in the marine science class on each attempt is m and the probability of enrolling successfully in CS 70 on each attempt is l. Also, these events are independent. (a) Suppose Lydia begins by attempting to enroll in the marine science class everyday and gets enrolled in it on day M. What is the distribution of M? (b) Suppose she is not enrolled in the marine science class after attempting each day for the first 5 days. What is the conditional distribution of M given M > 5? (c) Once she is enrolled in the marine science class, she starts attempting to enroll in CS 70 from day M +1 and gets enrolled in it on day C. Find the expected number of days it takes Lydia to enroll in both the classes, i.e. E[C]. (d) Suppose instead of attempting one by one, Lydia decides to attempt enrolling in both the classes from day 1. Let M be the number of days it takes to enroll in the marine science class, and C be the number of days it takes to enroll in CS 70. What is the distribution of M and C now? Are they independent? (e) Let X denote the day she gets enrolled in her first class and let Y denote the day she gets enrolled in both the classes. What is the distribution of X? (f) What is the expected number of days it takes Lydia to enroll in both classes now, i.e. E[Y]. (g) What is the expected number of classes she will be enrolled in by the end of 14 days? CS 70, Summer 2020, HW 6 3 3 Short Answer (a) Let X be uniform on the interval [0;2], and define Y = 2X +1. Find the PDF, CDF, expectation, and variance of Y. (b) Let X and Y have joint distribution f (x;y) = (cxy 0 else +1=4 x 2 [1;2] and y 2 [0;2] Find the constant c. Are X and Y independent? (c) Let X ∼ Exp(3). What is the probability that X 2 [0;1]? If I define a new random variable Y = bXc, for each k 2 N, what is the probability that Y = k? Do you recognize this (discrete) distribution? (d) Let Xi ∼ Exp(li) for i = 1;:::;n be mutually independent. It is a (very nice) fact that min(X1;:::;Xn) ∼ Exp(m). Find m. Solution: 4 Useful Uniforms Let X be a continuous random variable whose image is all of R; that is, P[X 2 (a;b)] > 0 for all a;b 2 R and a 6= b. (a) Give an example of a distribution that X could have, and one that it could not. (b) Show that the CDF F of X is strictly increasing. That is, F(x+e) > F(x) for any e > 0. Argue why this implies that F : R ! (0;1) must be invertible. (c) Let U be a uniform random variable on (0;1). What is the distribution of F-1(U)? (d) Your work in part (c) shows that in order to sample X, it is enough to be able to sample U. If X was a discrete random variable instead, taking finitely many values, can we still use U to sample X? Solution: 5 It’s Raining Fish A hurricane just blew across the coast and flung a school of fish onto the road nearby the beach. The road starts at your house and is infinitely long. We will label a point on the road by its distance from your house (in miles). For each n 2 N, the number of fish that land on the segment of the road [n;n + 1] is independently pois(l) and each fish that is flung into that segment of the road lands uniformly at random within the segment. Keep in mind that you can cite any result from lecture or discussion without proof. (a) What is the distribution of the number of fish arriving in segment [0;n] of the road, for some n 2 N. (b) Let [a;b] be an interval in [0;1]. What is the distribution of the number of fish that lands in the segment [a;b] of the road? (c) Let [a;b] be any interval such that a ≥ 0. What is the distribution of the number of fish that land in [a;b]? (d) Suppose you take a stroll down the road. What is the distribution of the distance you walk (in miles) until you encounter the first fish? Justify with proof. (e) Suppose you encounter a fish at distance x. What is the distribution of the distance you walk until you encounter the next fish? Solution: 6 Exponential Expectation (a) Let X ∼ Exp(l). Use induction to show that E[Xk] = k!=lk for every k 2 N. (b) For any jtj < l, compute E[etX] directly from the definition of expectation. (c) Using part (a), compute ∑¥ k=0 E[kX!k]tk. (d) Let M(t) = E[etX] be a function defined for all t such that jtj < l. What is dMdt(t) t=0 ? What is d2M(t) dt2 t=0 ? How does each of these relate to the mean and variance of an Exp(l) distribution? CS 70, Summer 2020, HW 6 9 7 Noisy Love Suppose you have confessed to your love interest on Valentine’s Day and you are waiting to hear back. Your love interest is trying to send you a binary message: “0” means that your love interest is not interested in you, while “1” means that your love interest reciprocates your feelings. Let X be your love interest’s message for you. Your current best guess of X has P(X = 0) = 0:7 and P(X = 1) = 0:3. Unfortunately, your love interest sends you the message through a noisy channel, and instead of receiving the message X, you receive the message Y = X +e, where e is independent Gaussian noise with mean 0 and variance 0:49. (a) First, you decide upon the following rule: if you observe Y > 0:5, then you will assume that your love interest loves you back, whereas if you observe Y ≤ 0:5, then you will assume that your love interest is not interested in you. What is the probability that you are correct using this rule? (Express your answer in terms of the CDF of the standard Gaussian distribution F(z) = P(N (0;1) ≤ z), and then evaluate your answer numerically.) (b) Suppose you observe Y = 0:6. What is the probability that your love interest loves you back? [Hint: This problem requires conditioning on an event of probability 0, namely, the event fY = 0:6g. To tackle this problem, think about conditioning on the event fY 2 [0:6;0:6 + d]g, where d > 0 is small, so that fY (0:6)·d ≈ P(Y 2 [0:6;0:6+ d]), and then apply Bayes Rule.] (c) Suppose you observe Y = y. For what values is it more likely than not that your love interest loves you back? [Hint: As before, instead of considering fY = yg, you can consider the event fY 2 [y;y + d]g for small d > 0. So, when is P(X = 1 j Y 2 [y;y + d]) ≥ P(X = 0 j Y 2 [y;y+ d])?] (d) Your new rule is to assume that your love interest loves you back if (based on the value of Y that you observe) it is more likely than not that your love interest loves you back. Under this new rule, what is the probability that you are correct? Solution: 8 Sum of Independent Gaussians In this question, we will introduce an important property of the Gaussian distribution: the sum of independent Gaussians is also a Gaussian. Let X and Y be independent standard Gaussian random variables. Recall that the density of the standard Gaussian is f (x) = p12p exp -x22 : (a) What is the joint density of X and Y? (b) Observe that the joint density of X and Y, fX;Y (x;y), only depends on the quantity x2 + y2, which is the distance from the origin. In other words, the Gaussian is rotationally symmetric. Next, we will try to find the density of X +Y. To do this, draw a picture of the Cartesian plane and draw the region x + y ≤ c, where c is a real number of your choice. CS 70, Summer 2020, HW 6 12 (c) Now, rotate your picture clockwise by p=4 so that the line X +Y = c is now vertical. Redraw your figure. Let X0 and Y0 denote the random variables which correspond to the p=4 clockwise rotation of (X;Y) and express the new shaded region in terms of X0 and Y0. (d) By rotational symmetry of the Gaussian, (X0;Y0) has the same distribution as (X;Y). Argue that X +Y has the same distribution as p2Z, where Z is a standard Gaussian. This proves the following important fact: the sum of independent Gaussians is also a Gaussian. Notice that X ∼ N (0;1), Y ∼ N (0;1) and X +Y ∼ N (0;2). In general, if X and Y are independent Gaussians, then X +Y is a Gaussian with mean mX + mY and variance sX2 +sY2. (e) Recall the CLT: If fXigi2N is a sequence of i.i.d. random variables with mean m 2 R and variance s2 < ¥, then: X1 +···+Xn -nm spn in distribution -------! N (0;1) as n ! ¥: Prove that the CLT holds for the special case when the Xi are i.i.d. N (0;1). [Show More]

Last updated: 1 year ago

Preview 1 out of 14 pages