CS221 Exam 2018 ( ALL SOLUTIONS ARE 100% CORRECT )

Document Content and Description Below

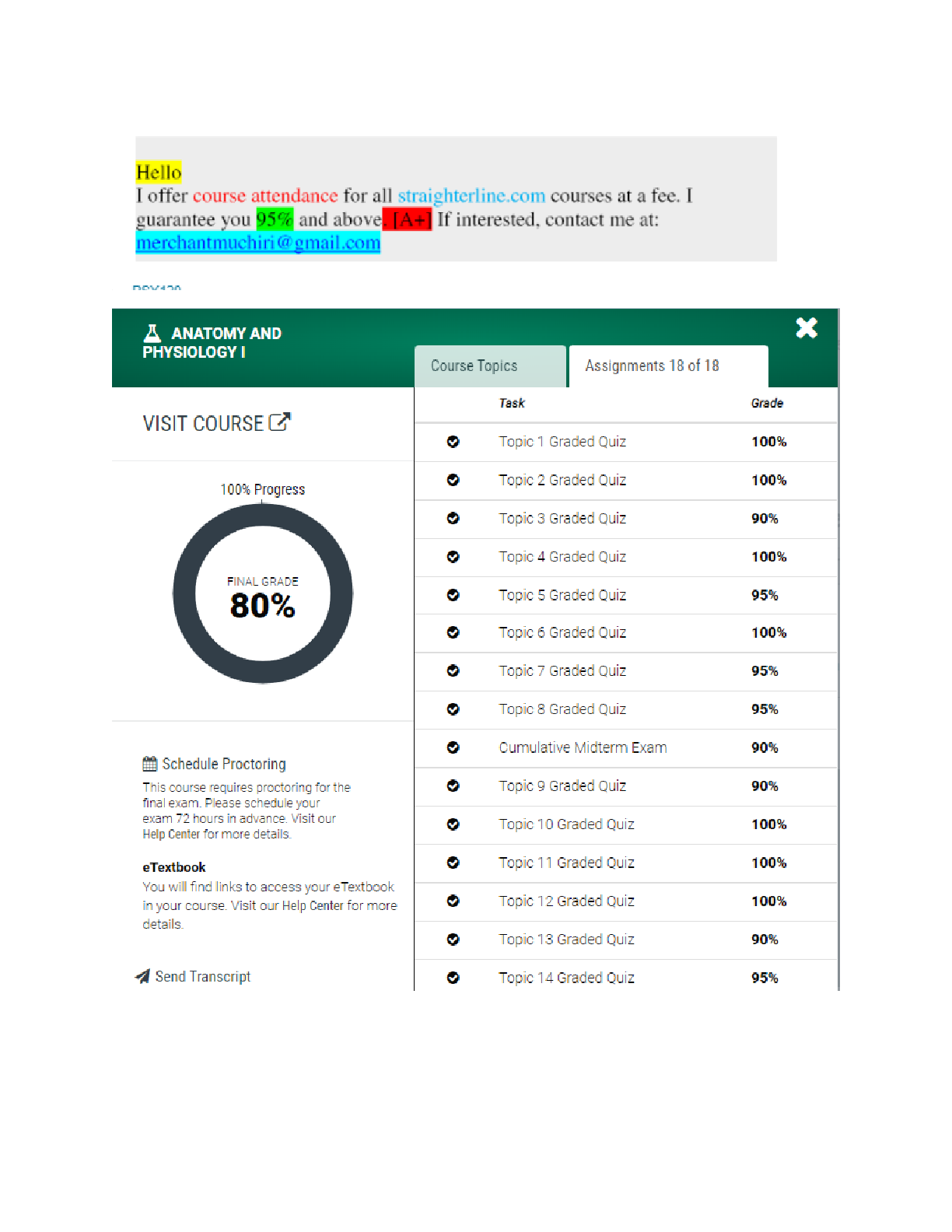
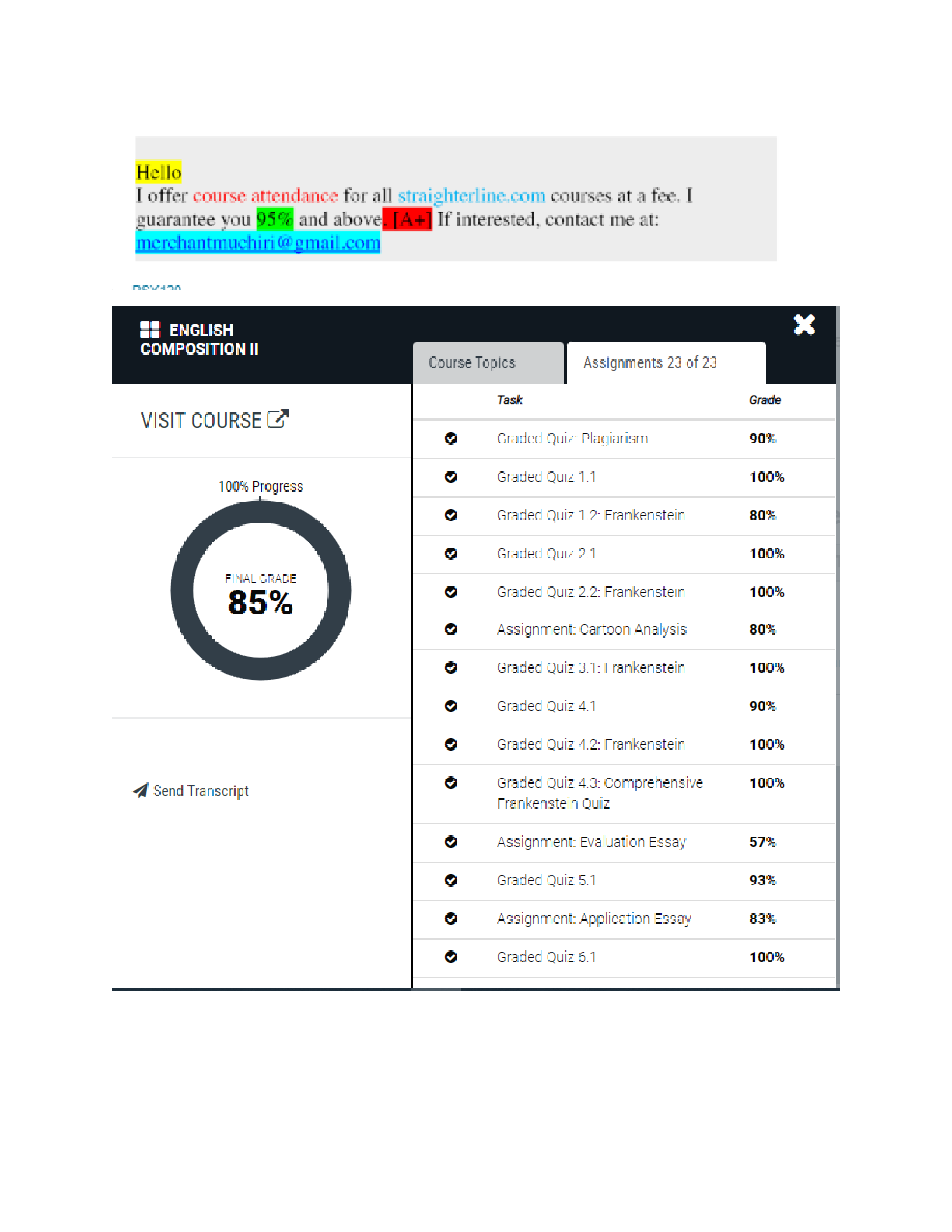
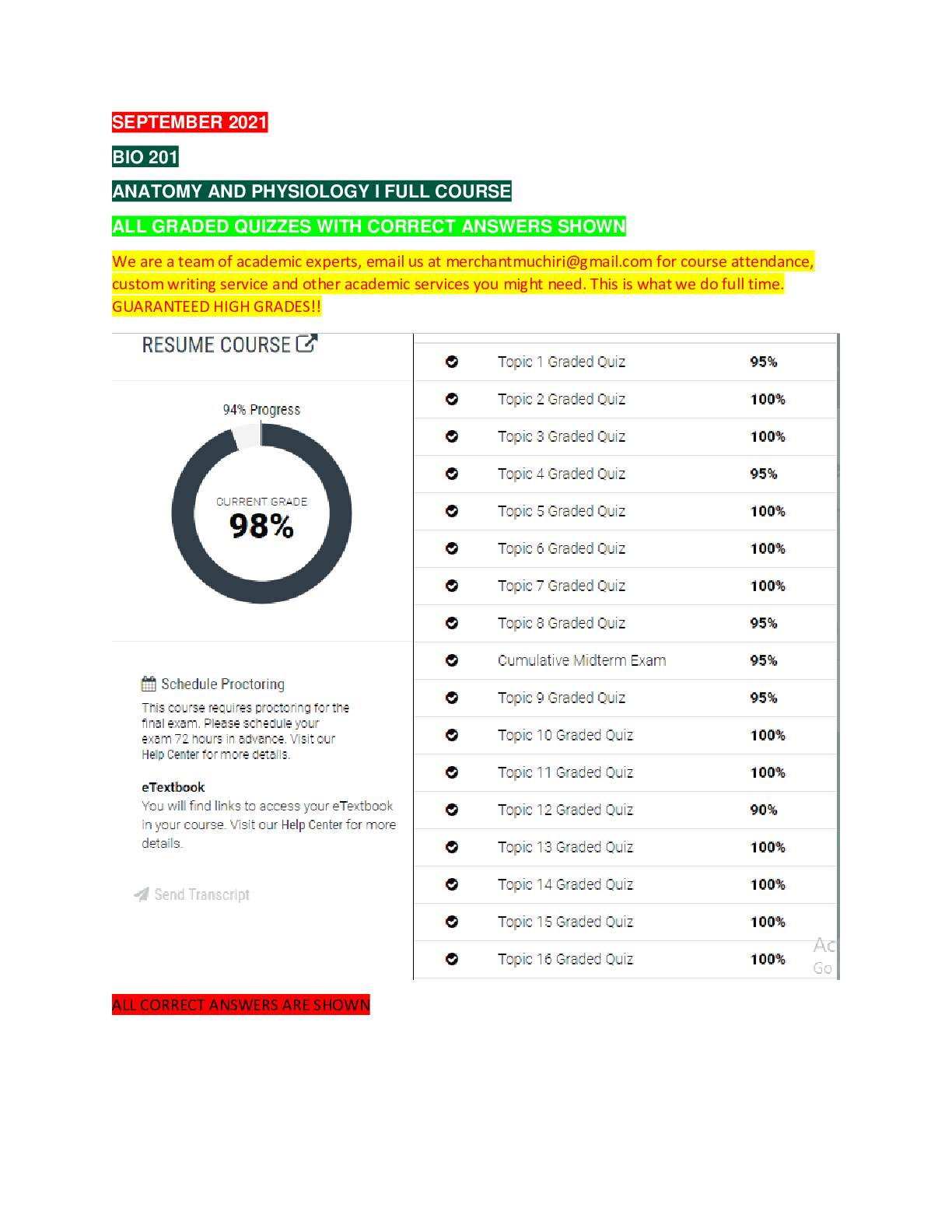
CS221 Exam Solutions CS221 November 27, 2018 Name: | {z } by writing my name I agree to abide by the honor code SUNet ID: Read all of the following information before starting the exam: • Thi... s test has 3 problems and is worth 150 points total. It is your responsibility to make sure that you have all of the pages. • Keep your answers precise and concise. Show all work, clearly and in order, or else points will be deducted, even if your final answer is correct. • Don’t spend too much time on one problem. Read through all the problems carefully and do the easy ones first. Try to understand the problems intuitively; it really helps to draw a picture. • You cannot use any external aids except one double-sided 81 2" x 11" page of notes. • Good luck! Problem Part Max Score Score 1 a 10 b 10 c 10 d 10 e 10 2 a 10 b 10 c 10 d 10 e 10 3 a 10 b 10 c 10 d 10 e 10 Total Score: + + = 11. Wildlife (50 points) You are working in a wildlife conservation group, where you are installing n sensors to detect the presence of a wild animal called a pangolin. Let Y 2 f0; 1g denote whether there is actually a pangolin (in the given location), and let X1; : : : ; Xn denote the predicted outputs of the n sensors, where each Xi 2 f0; 1g. We assume the following: • There is a natural rate of pangolin appearance p(y = 1) = h. • All sensors have the same false positive rate of p(xi = 1 j y = 0) = α. • All sensors have the same false negative rate of p(xi = 0 j y = 1) = β. • All sensor outputs are conditionally independent given the actual appearance (see Figure ??). Figure 1: A Bayesian network with n = 4 sensors relating the presence of a pangolin Y and sensor outputs X1; : : : ; X4. 2a. (10 points) The specification sheet for the sensors does not provide the false positive rates or the false negative rates, so you have to estimate them. Each week, you install a new sensor, and record all the outputs of all the sensors installed thus far. Then you go out into the field and observe whether there is a pangolin or not (Y ). Below is the data you have collected, where \-" indicates there is no data for that sensor for that week. X1 X2 X3 X4 Y Week 1 0 - - - 0 Week 2 0 1 - - 0 Week 3 1 1 0 - 1 Week 4 0 0 1 0 0 Compute the maximum likelihood estimate of the parameters (h; α; β) of the Bayesian network: h = α = β = Solution The maximum likelihood solution has a closed form which can be computed by simply counting and normalizing: h = number of Y = 1 total number of weeks = 1 4 ; (1) α = number of Y = 0 ^ Xi = 1 number of Y = 0 = 2 7 ; (2) β = number of Y = 1 ^ Xi = 0 number of Y = 1 = 1 3 : (3) Note that each week gives rise to a variable number of counts, but this does not matter. 3b. (10 points) After experiencing the dangers of data collection in the wild for four weeks, you decide that it’s not really your true calling. Instead, you’re just going to use your estimated parameters (h; α; β) to predict Y for future weeks. Suppose that you have n sensors installed. During one week, you observe that all the sensors output 1. What is P(Y = 1 j X1 = · · · = Xn = 1), i.e. the probability that there is a pangolin given the observations? Your answer should be an expression defined in terms of (h; α; β; n). Solution Let’s compute a more general answer where 0 ≤ k ≤ n of the sensors output 1. Consider Y = 1. For each of the k Xi’s that are observed to be 1, we have p(xi = 1 j y = 1) = 1−β. For the rest of the n−k Xi’s that are observed to be 0, we have p(xi = 0 j y = 1) = β. We can do an analogous calculation for Y = 0 with α instead of β. The result is as follows: P(Y = 1 j X1 = x1; : : : ; Xn = xn) (4) = p(y = 1) Qn i=1 p(xi j y = 1) p(y = 1) Qn i=1 p(y = 1 j xi) + p(y = 0) Qn i=1 p(xi j y = 0) (5) = h(1 − β)kβn−k h(1 − β)kβn−k + (1 − h)αk(1 − α)n−k (6) = h(1 − β)n h(1 − β)n + (1 − h)αn ; (7) where in the last line, we used the fact that k = n. [Show More]

Last updated: 1 year ago

Preview 1 out of 24 pages