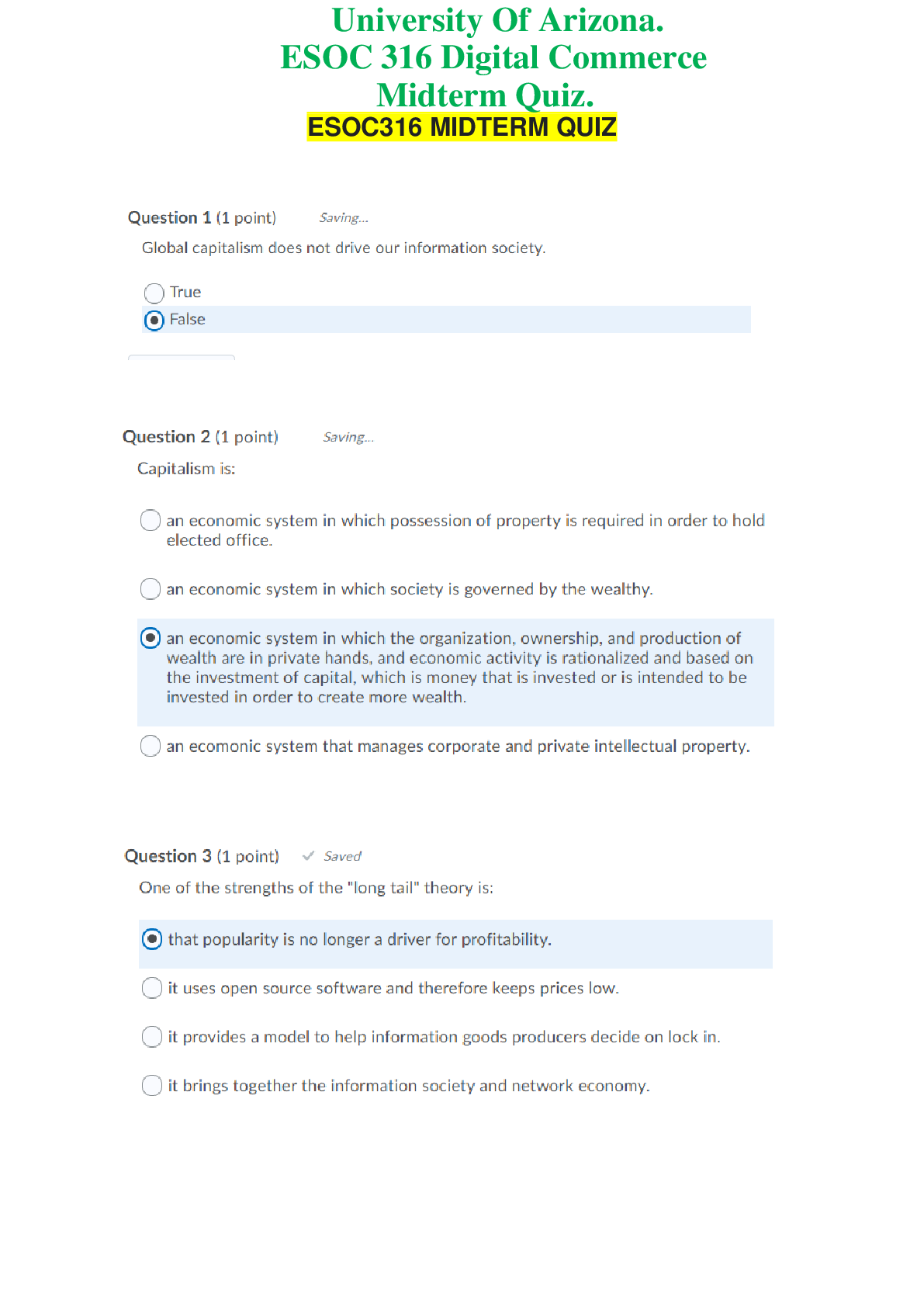
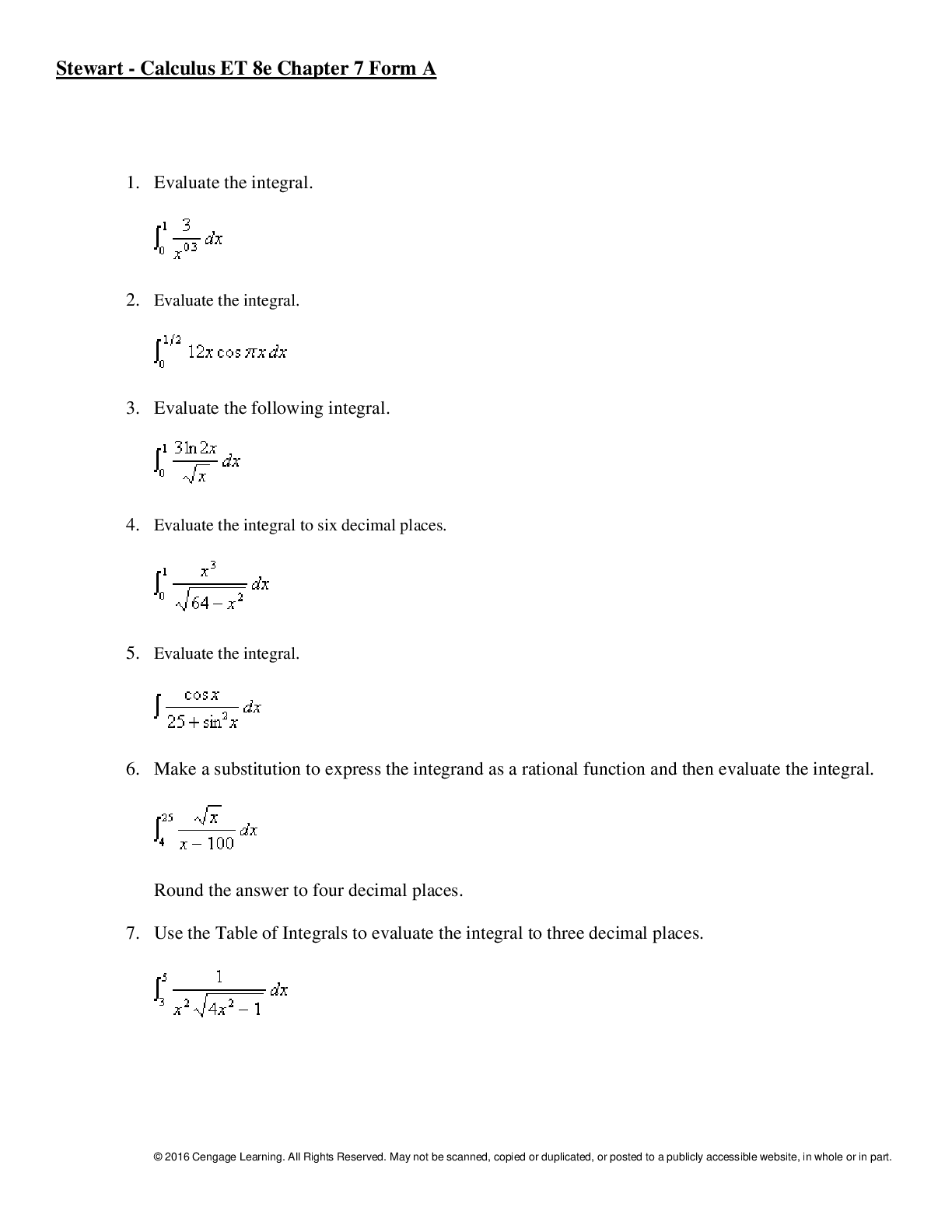
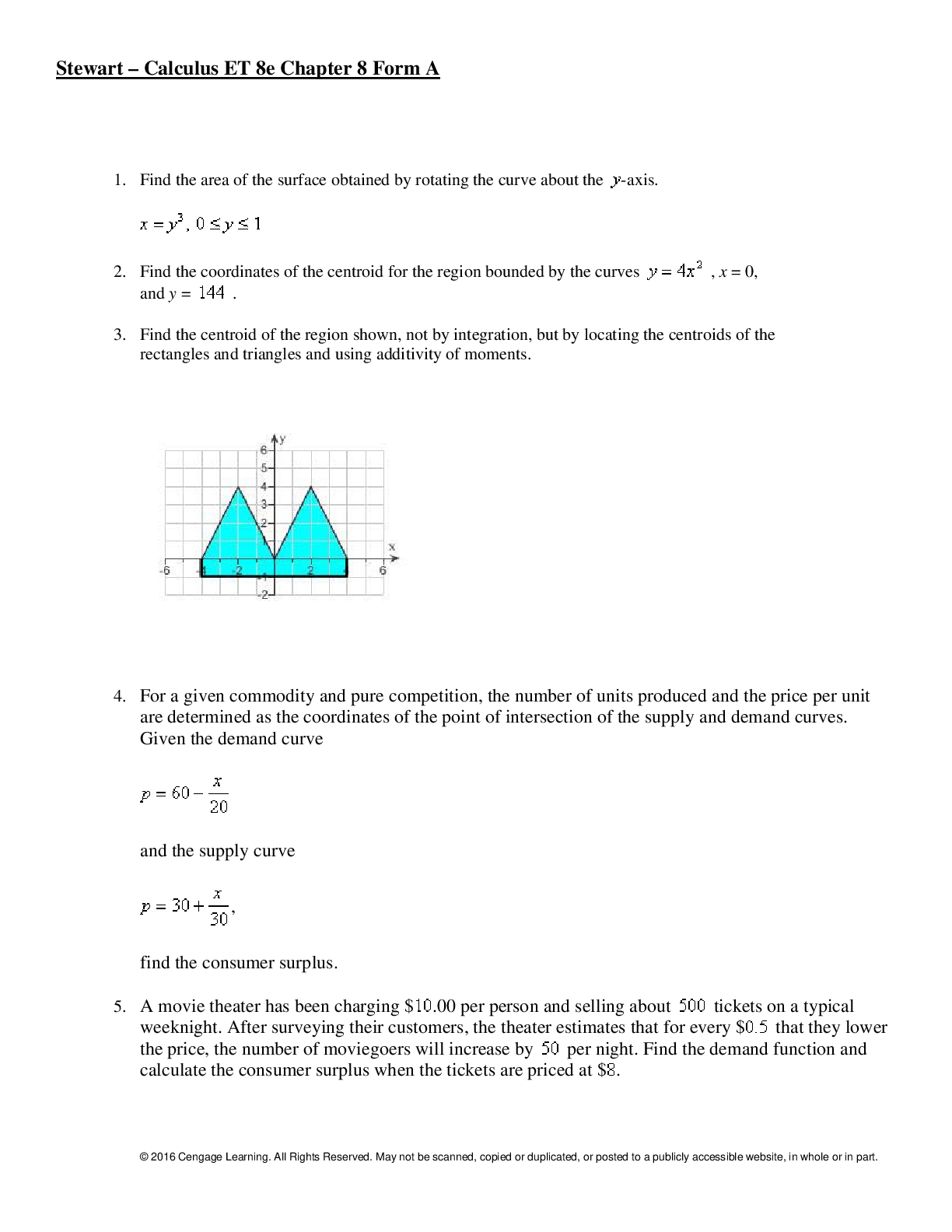
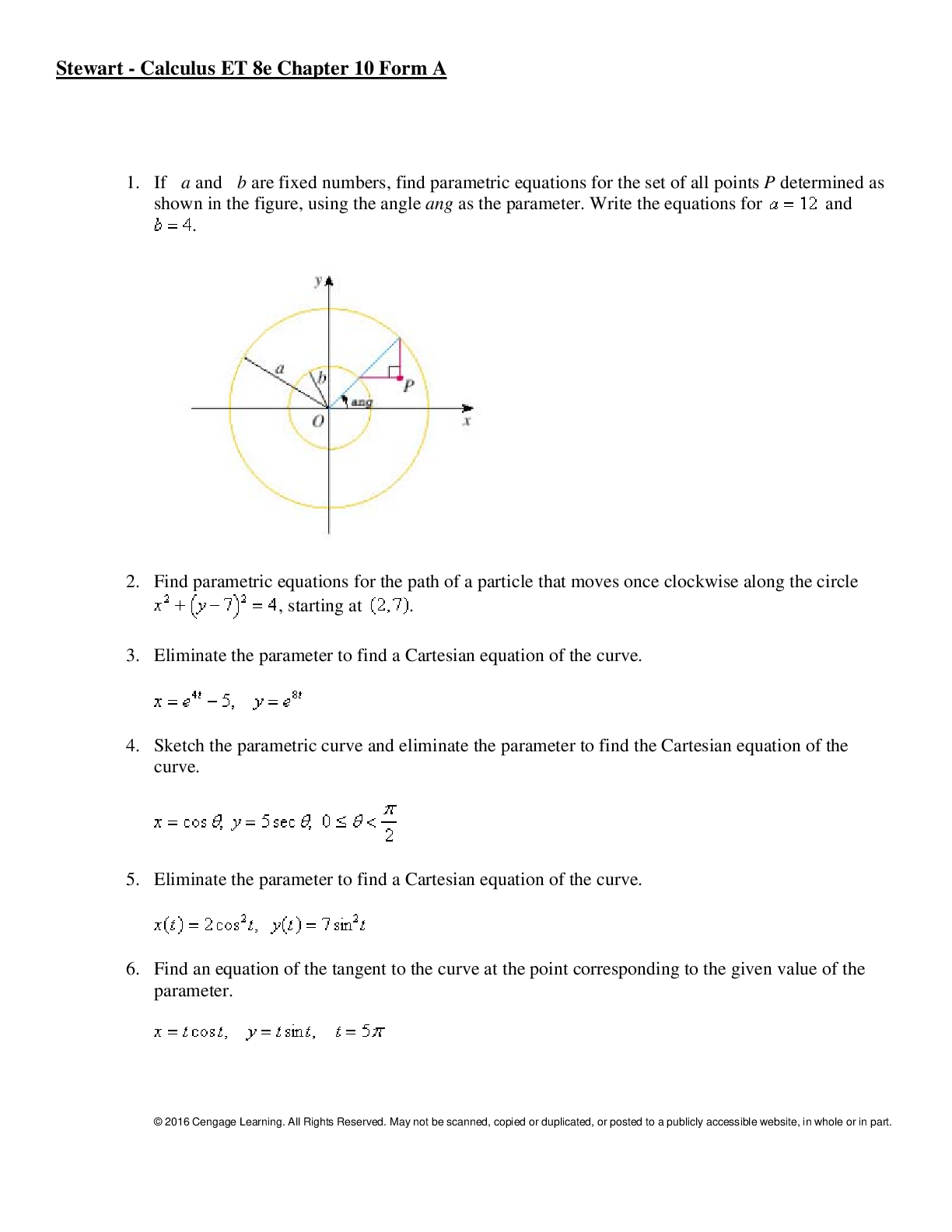
Calculus > QUESTIONS & ANSWERS > Stewart - Calculus ET 8e Chapter 16. All Answers (All)
Stewart - Calculus ET 8e Chapter 16. All Answers
Document Content and Description Below
1. Find the work done by the force field in moving an object along an arch of the cycloid 2. Find the exact value of where C is the line segment from (0, 0, 0) to (1, , ). 3. Determine whether or n... ot vector field is conservative. If it is conservative, find a function f such that 4. Find the curl of the vector field. 5. Find the curl of the vector field. 6. Determine whether or not vector field is conservative. If it is conservative, find a function f such that 7. Use Stoke’s theorem to evaluate C is the curve of intersection of the plane z = x + 9 and the cylinder 8. Use Stoke’s theorem to evaluate C is the curve of intersection of the hyperbolic paraboloid and the cylinder oriented counterclockwise as viewed from above. 9. Find parametric equations for C, if C is the curve of intersection of the hyperbolic paraboloid and the cylinder oriented counterclockwise as viewed from above. 10. Find the area of the part of paraboloid that lies inside the cylinderStewart - Calculus ET 8e Chapter 16 Form A © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 11. Evaluate the line integral over the given curve C. , where C is the line segment joining (–4, –5) to (5, 4) 12. Evaluate the line integral over the given curve C. , where C is the line segment joining (–2, –1) to (4, 5) 13. A thin wire in the shape of a quarter-circle , , has a linear mass density . Find the mass and the location of the center of mass of the wire. 14. The plot of a vector field is shown below. A particle is moved . By inspection, determine whether the work done by F on the particle is positive, negative, or zero. 15. Determine whether F is conservative. If so, find a function f such that . 16. Determine whether F is conservative. If so, find a function f such that . 17. Let f be a scalar field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field.Stewart - Calculus ET 8e Chapter 16 Form A © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 18. Find the area of the surface S where S is the part of the surface that lies inside the cylinder 19. Find the area of the surface S where S is the part of the sphere that lies to the right of the xz-plane and inside the cylinder 20. Find a vector representation for the surface. The plane that passes through the point and contains the vectors and .Stewart - Calculus ET 8e Chapter 16 Form A © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. 2. 3. 4. 5. 6. 7. 8. 9. 10. 11. 234 12. 120 13. mass = 216; Center of mass = 14. positive 15. 16. The vector field is not conservative. There exists no scalar field f such that 17. The vector grad f is defined. It is the gradient (vector) field F of the scalar field f. So, , which is not meaningful. 18. 19. 20. Answers may vary.Stewart - Calculus ET 8e Chapter 15 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 1. Find the gradient vector field of 2. Consider the vector field If a particle starts at the point in the velocity field given by F, find an equation of the path it follows. 3. Find the work done by the force field in moving an object along an arch of the cycloid 4. Calculate the work done by the force field when a particle moves under its influence around the edge of the part of the sphere that lies in the first octant, in a counterclockwise direction as viewed from above. 5. Determine whether or not F is a conservative vector field. If it is, find a function f such that 6. Find a function f such that , and use it to evaluate along the given curve C. 7. Find a function f such that and use it to evaluate along the given curve C. C is the upper semicircle that starts at (1, 2) and ends at (5, 2).Stewart - Calculus ET 8e Chapter 15 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 8. Use Green's Theorem to find the work done by the force in moving a particle from the origin along the x-axis to (1, 0) then along the line segment to (0, 1) and then back to the origin along the y-axis. 9. Evaluate the line integral. 10. Find the curl of . 11. Determine whether or not vector field is conservative. If it is conservative, find a function f such that 12. Determine whether or not vector field is conservative. If it is conservative, find a function f such that 13. Find the moment of inertia about the z-axis of a thin funnel in the shape of a cone if its density function is 14. Use Stoke’s theorem to evaluate C is the curve of intersection of the hyperbolic paraboloid and the cylinder oriented counterclockwise as viewed from above. 15. Find a parametric representation for the part of the plane that lies inside the cylinder 16. Evaluate the line integral over the given curve C. , where C is the line segment joining (–5, –7) to (3, 1)Stewart - Calculus ET 8e Chapter 15 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 17. Determine whether F is conservative. If so, find a function f such that . 18. Find (a) the divergence and (b) the curl of the vector field F. 19. Let f be a scalar field. Determine whether the expression is meaningful. If so, state whether the expression represents a scalar field or a vector field. 20. Use Stokes’ Theorem to evaluate . ; S is the part of the ellipsoid lying above the xy-plane and oriented with normal pointing upward.Stewart - Calculus ET 8e Chapter 15 Form B © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. 2. 3. 4. 1536 5. 6. 4 7. 8 8. 9. 10. 11. 12. 13. 14. 15. 16. 200 17. The vector field is not conservative. There exists no scalar field f such that 18. (a). (b). 19. The vector grad f is defined. It is the gradient (vector) field F of the scalar field f. So, , which is not meaningful. 20. 0Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Select the correct answer for each question. ____ 1. Find the gradient vector field of f. a. b. c. d. e. None of these ____ 2. Find the gradient vector field of the scalar function f. (That is, find the conservative vector field F for the potential function f of F.) a. b. c. d.Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 3. Evaluate the line integral where and C is the arc of the circle traversed counterclockwise from ( , 0) to (0, ). Round your answer to two decimal places. a. b. c. d. e. ____ 4. Find the exact mass of a thin wire in the shape of the helix if the density is 5. a. b. c. d. e. ____ 5. Find the work done by the force field on a particle that moves along the parabola a. b. c. d. e.Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 6. Evaluate the line integral over the given curve C. ; , a. 92 b. 69 2 c. 231 2 d. 81 2 ____ 7. Evaluate the line integral over the given curve C. ; , a. 28 b. 26 c. 40 d. 97 3 ____ 8. Evaluate , where C is given by Round your answer to two decimal place. a. b. c. d. e.Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 9. Show that F is conservative, and find a function f such that , and use the result to evaluate , where C is any curve from to . ; and a. 0 b. –154 c. –107 d. –89 ____ 10. Let D be a region bounded by a simple closed path C in the xy. Then the coordinates of the centroid where A is the area of D. Find the centroid of the triangle with vertices (0, 0), ( , 0) and (0, ). a. b. c. d. e.Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 11. Use Green’s Theorem to evaluate the line integral along the positively oriented closed curve C. , where C is the cardioid . a. 20 b. –80 c. 10 d. 40 ____ 12. A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and . a. b. c. d. e.Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 13. Below is given the plot of a vector field F in the xy-plane. (The z-component of F is 0.) By studying the plot, determine whether div F is positive, negative, or zero. a. cannot be determined b. negative c. zero d. positive ____ 14. Find the curl of the vector field F. a. b. c. d. ____ 15. Suppose that where g is a function of one variable such that . Evaluate where S is the sphere a. b. c. d. e. None of theseStewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 16. Evaluate . ; S is the part of the plane in the first octant. a. 72 29 b. 0 c. 403 d. 273 ____ 17. Evaluate . ; S is the part of the cone between the planes and . a. b. c. 70 3 d. 0 ____ 18. Evaluate . ; S is the part of the torus with vector representation , , . a. 0 b. c. d.Stewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Find the mass of the surface S having the given mass density. S is part of the plane in the first octant; the density at a point P on S is equal to the square of the distance between P and the xy-plane. a. 42 b. c. 19 d. ____ 20. Let S be the cube with vertices . Approximate by using a Riemann sum as in Definition 1, taking the patches to be the squares that are the faces of the cube and the points to be the centers of the squares. a. b. c. d. e. none of theseStewart - Calculus ET 8e Chapter 15 Form C © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. B 2. C 3. D 4. C 5. C 6. B 7. D 8. B 9. A 10. B 11. A 12. B 13. B 14. C 15. D 16. A 17. C 18. B 19. D 20. CStewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Select the correct answer for each question. ____ 1. Which plot illustrates the vector field a. c. b. d. ____ 2. Find the exact mass of a thin wire in the shape of the helix if the density is 5. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 3. Find the work done by the force field F on a particle that moves along the curve C. ; , a. 17 b. 19 c. 34 d. 71 2 ____ 4. Evaluate where C is the right half of the circle a. b. c. d. e. ____ 5. Evaluate for the vector field F and the path C. (Hint: Show that F is conservative, and pick a simpler path.) C: a. 24 b. 47 c. 0 d.Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 6. Show that F is conservative, and find a function f such that , and use the result to evaluate , where C is any curve from to . ; and a. –89 b. 0 c. –154 d. –107 ____ 7. Show that F is conservative and find a function f such that , and use this result to evaluate , where C is any path from to . ; and a. b. c. d. ____ 8. Use Green's Theorem and/or a computer algebra system to evaluate where C is the circle with counterclockwise orientation. a. b. c. d. e. None of theseStewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 9. Use Green’s Theorem to evaluate the line integral along the positively oriented closed curve C. , where C is the triangle with vertices , , and . a. 6 b. 60 c. 30 d. 66 ____ 10. Use Green’s Theorem to find the work done by the force in moving a particle in the positive direction once around the triangle with vertices , , and . a. 7 b. 7 6 c. 7 3 d. 42 ____ 11. A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and . a. b. c. d. e.Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 12. Find the correct identity, if f is a scalar field, F and G are vector fields. a. b. c. d. None of these ____ 13. Let a. 5 b. 3 c. 1 d. 2 e. None of these ____ 14. Evaluate the surface integral. Round your answer to four decimal places. S is surface a. b. c. d. e.Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 15. Let S be the cube with vertices . Approximate by using a Riemann sum as in Definition 1, taking the patches to be the squares that are the faces of the cube and the points to be the centers of the squares. a. b. c. d. e. none of these ____ 16. Use Stokes’ Theorem to evaluate . ; C is the curve obtained by intersecting the cylinder with the hyperbolic paraboloid , oriented in a counterclockwise direction when viewed from above a. b. 0 c. d. 1Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 17. Use a computer algebra system to compute the flux of F across S. S is the surface of the cube cut from the first octant by the planes a. b. c. d. e. ____ 18. Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find , where a is the constant vector. a. 8 b. 6 c. 5 d. 7 e. 0Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Find the area of the surface. The part of the paraboloid ; , a. b. c. d. ____ 20. Find a parametric representation for the part of the elliptic paraboloid that lies in front of the plane x = 0. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 16 Form D © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. A 2. D 3. C 4. C 5. D 6. B 7. B 8. D 9. C 10. C 11. D 12. A 13. B 14. C 15. C 16. A 17. D 18. E 19. B 20. DStewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Match the vector field with its plot. Select the correct answer. a. c. b. d. 2. Find the gradient vector field of the scalar function f. (That is, find the conservative vector field F for the potential function f of F.)Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 3. Find the exact mass of a thin wire in the shape of the helix if the density is 5. Select the correct answer. a. b. c. d. e. 4. Evaluate the line integral over the given curve C. ; , ____ 5. A thin wire is bent into the shape of a semicircle If the linear density is , find the exact mass of the wire. Select the correct answer. a. b. c. d. e. ____ 6. Show that F is conservative, and find a function f such that , and use the result to evaluate , where C is any curve from to . ; and Select the correct answer. a. –89 b. 0 c. –154 d. –107Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 7. Let where . Which of the following equations does the line segment from to satisy? Select the correct answer. a. b. c. none of these 8. Use Green’s Theorem to find the work done by the force in moving a particle in the positive direction once around the triangle with vertices , , and . ____ 9. A particle starts at the point , moves along the x-axis to (3, 0) and then along the semicircle to the starting point. Use Green's Theorem to find the work done on this particle by the force field Select the correct answer. a. b. c. 0 d. e. 10. A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and .Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 11. Below is given the plot of a vector field F in the xy-plane. (The z-component of F is 0.) By studying the plot, determine whether div F is positive, negative, or zero. Select the correct answer. a. cannot be determined b. zero c. negative d. positive ____ 12. Find the divergence of the vector field F. Select the correct answer. a. b. c. d. 13. Find the curl of the vector field F.Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 14. The temperature at the point in a substance with conductivity is Find the rate of heat flow inward across the cylindrical Select the correct answer. a. b. c. d. e. 15. Let S be the cube with vertices . Approximate by using a Riemann sum as in Definition 1, taking the patches to be the squares that are the faces of the cube and the points to be the centers of the squares.Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 16. Use the Divergence Theorem to calculate the surface integral ; that is, calculate the flux of across . S is the surface of the box bounded by the coordinate planes and the planes . Select the correct answer. a. b. 25 2 c. d. 2 25 e. 17. Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find , where a is the constant vector. 18. Find the area of the surface. The part of the paraboloid ; ,Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Find a parametric representation for the part of the elliptic paraboloid that lies in front of the plane x = 0. Select the correct answer. a. b. c. d. e. 20. Find the area of the part of the surface that lies between the planes x = 0, x = 4, , and z = 1.Stewart - Calculus ET 8e Chapter 16 Form E © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. C 2. 3. D 4. 1 7 5. B 6. B 7. B 8. 3 9. D 10. 11. D 12. A 13. 14. E 15. 16. B 17. 0 18. 19. B 20.Stewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Find the gradient vector field of f. Select the correct answer. a. b. c. d. e. None of these 2. Find the gradient vector field of the scalar function f. (That is, find the conservative vector field F for the potential function f of F.) 3. Evaluate the line integral over the given curve C. ; ,Stewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 4. Find the work done by the force field F on a particle that moves along the curve C. Select the correct answer. ; , a. 17 b. 19 c. 34 d. 71 2 5. Determine whether F is conservative. If so, find a function f such that . 6. Show that F is conservative and find a function f such that , and use this result to evaluate , where C is any path from to . ; and ____ 7. Show that F is conservative, and find a function f such that , and use the result to evaluate , where C is any curve from to . ; and Select the correct answer. a. 224 b. 135 c. 117 d. 70Stewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 8. Use Green’s Theorem to find the work done by the force in moving a particle in the positive direction once around the triangle with vertices , , and . Select the correct answer. a. 7 b. 7 6 c. 7 3 d. 42 9. Find the curl of the vector field F. ____ 10. Find the curl of the vector field. Select the correct answer. a. b. c. d. e. None of theseStewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 11. Find the value of the constant c such that the vector field is the curl of some vector field F. ____ 12. Evaluate the surface integral. Round your answer to four decimal places. S is surface Select the correct answer. a. b. c. d. e. ____ 13. Evaluate . ; S is the part of the torus with vector representation , , . Select the correct answer. a. 0 b. c. d. 14. Find the mass of the surface S having the given mass density. S is the hemisphere , ; the density at a point P on S is equal to the distance between P and the xy-plane.Stewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 15. Evaluate the surface integral where S is the surface with parametric equations , . Select the correct answer. a. b. c. d. e. 16. Use Stokes’ Theorem to evaluate . ; S is the part of the paraboloid lying below the plane and oriented with normal pointing downward. ____ 17. Use Stoke’s theorem to evaluate where and C is the boundary of the part of the plane in the first octant. Select the correct answer. a. 69 b. 16 c. 49 d. 0 e. 23 18. Use the Divergence Theorem to calculate the surface integral ; that is, calculate the flux of across . S is the surface of the box bounded by the coordinate planes and the planes .Stewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Match the equation with one of the graphs below. a. c. b. d. ____ 20. Find the area of the part of the surface that lies between the planes x = 0, x = 4, , and z = 1. Select the correct answer. a. b. c. d. e.Stewart – Calculus ET 8e Chapter 16 Form F © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. D 2. 3. 1 7 4. C 5. 6. 7. A 8. C 9. 10. A 11. –8 12. C 13. B 14. 15. A 16. 0 17. D 18. 18 19. D 20. AStewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Which plot illustrates the vector field a. c. b. d. 2. Find the gradient vector field of f. 3. Find the gradient vector field of the scalar function f. (That is, find the conservative vector field F for the potential function f of F.) 4. Find the exact mass of a thin wire in the shape of the helix if the density is 4.Stewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 5. Find the work done by the force field on a particle that moves along the parabola Select the correct answer. a. b. c. d. e. 6. Evaluate the line integral over the given curve C. ; ,Stewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 7. Find the work done by the force field F on a particle that moves along the curve C. Select the correct answer. ; , a. 85 6 b. 3 c. 13 2 d. 13 ____ 8. Determine whether F is conservative. If so, find a function f such that . Select the correct answer. a. b. not conservative c. d. 9. Use Green’s Theorem to evaluate the line integral along the positively oriented closed curve C. , where C is the triangle with vertices , , and .Stewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 10. Let Select the correct answer. a. 6 b. 12 c. 18 d. 30 e. None of these 11. Below is given the plot of a vector field F in the xy-plane. (The z-component of F is 0.) By studying the plot, determine whether div F is positive, negative, or zero. ____ 12. Suppose that where g is a function of one variable such that . Evaluate where S is the sphere Select the correct answer. a. b. c. d. e. None of theseStewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 13. Evaluate the surface integral. S is the part of the plane that lies in the first octant. 14. Evaluate the surface integral. Round your answer to four decimal places. S is surface 15. Evaluate , that is, find the flux of F across S. ; S is the hemisphere ; n points upward. ____ 16. Let S be the cube with vertices . Approximate by using a Riemann sum as in Definition 1, taking the patches to be the squares that are the faces of the cube and the points to be the centers of the squares. Select the correct answer. a. b. c. d. e. none of theseStewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 17. Use Stokes’ Theorem to evaluate . ; S is the part of the paraboloid lying below the plane and oriented with normal pointing downward. 18. Use Stoke’s theorem to evaluate where and C is the boundary of the part of the plane in the first octant. ____ 19. Use a computer algebra system to compute the flux of F across S. S is the surface of the cube cut from the first octant by the planes Select the correct answer. a. b. c. d. e. 20. Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find , where a is the constant vector.Stewart - Calculus ET 8e Chapter 16 Form G © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. B 2. 3. 4. 5. E 6. 2 21 7. D 8. B 9. 50 10. C 11. zero 12. D 13. 14. 15. 16 3 16. C 17. 0 18. 0 19. B 20. 0Stewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 1. Match the vector field with its plot. a. c. b. d. 2. Find the work done by the force field on a particle that moves along the parabolaStewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 3. Find the work done by the force field F on a particle that moves along the curve C. ; , ____ 4. A thin wire is bent into the shape of a semicircle If the linear density is , find the exact mass of the wire. Select the correct answer. a. b. c. d. e. 5. Determine whether F is conservative. If so, find a function f such that . 6. Show that F is conservative and find a function f such that , and use this result to evaluate , where C is any path from to . ; and ____ 7. Show that F is conservative and find a function f such that , and use this result to evaluate , where C is any path from to . ; and Select the correct answer. a. b. c. d.Stewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. 8. Let D be a region bounded by a simple closed path C in the xy. Then the coordinates of the centroid where A is the area of D. Find the centroid of the triangle with vertices (0, 0), ( , 0) and (0, ). ____ 9. A plane lamina with constant density occupies a region in the xy-plane bounded by a simple closed path C. Its moments of inertia about the axes are Find the moments of inertia about the axes, if C is a rectangle with vertices (0, 0), (4, 0), (4, 5) and . Select the correct answer. a. b. c. d. e. 10. LetStewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 11. Below is given the plot of a vector field F in the xy-plane. (The z-component of F is 0.) By studying the plot, determine whether div F is positive, negative, or zero. a. zero b. cannot be determined c. negative d. positive ____ 12. Evaluate the surface integral. S is the part of the plane that lies in the first octant. Select the correct answer. a. b. c. d. e. 13. Find the mass of the surface S having the given mass density. S is part of the plane in the first octant; the density at a point P on S is equal to the square of the distance between P and the xy-plane.Stewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 14. Find the mass of the surface S having the given mass density. S is the hemisphere , ; the density at a point P on S is equal to the distance between P and the xy-plane. Select the correct answer. a. b. c. 64 d. 15. Let S be the cube with vertices . Approximate by using a Riemann sum as in Definition 1, taking the patches to be the squares that are the faces of the cube and the points to be the centers of the squares. 16. Evaluate the surface integral where S is the surface with parametric equations , . ____ 17. , where S consists of the hemisphere and the disk in the -plane. Select the correct answer. a. b. c. d. e. 18. Assuming that S satisfies the conditions of the Divergence Theorem and the scalar functions and components of the vector fields have continuous second order partial derivatives, find , where a is the constant vector.Stewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. ____ 19. Match the equation with one of the graphs below. a. c. b. d. 20. Find the area of the part of the surface that lies between the planes x = 0, x = 4, , and z = 1.Stewart - Calculus ET 8e Chapter 16 Form H © 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied or duplicated, or posted to a publicly accessible website, in whole or in part. Answer Key 1. D 2. 3. 55 3 4. E 5. 6. 7. D 8. 9. D 10. 3 11. D 12. C 13. 14. B 15. 16. 17. D 18. 0 19. B 20. [Show More]
Last updated: 1 year ago
Preview 1 out of 55 pages
Instant download

Buy this document to get the full access instantly
Instant Download Access after purchase
Add to cartInstant download
Reviews( 0 )
Document information
Connected school, study & course
About the document
Uploaded On
Jan 15, 2020
Number of pages
55
Written in
Additional information
This document has been written for:
Uploaded
Jan 15, 2020
Downloads
0
Views
42