Self Quiz

Document Content and Description Below

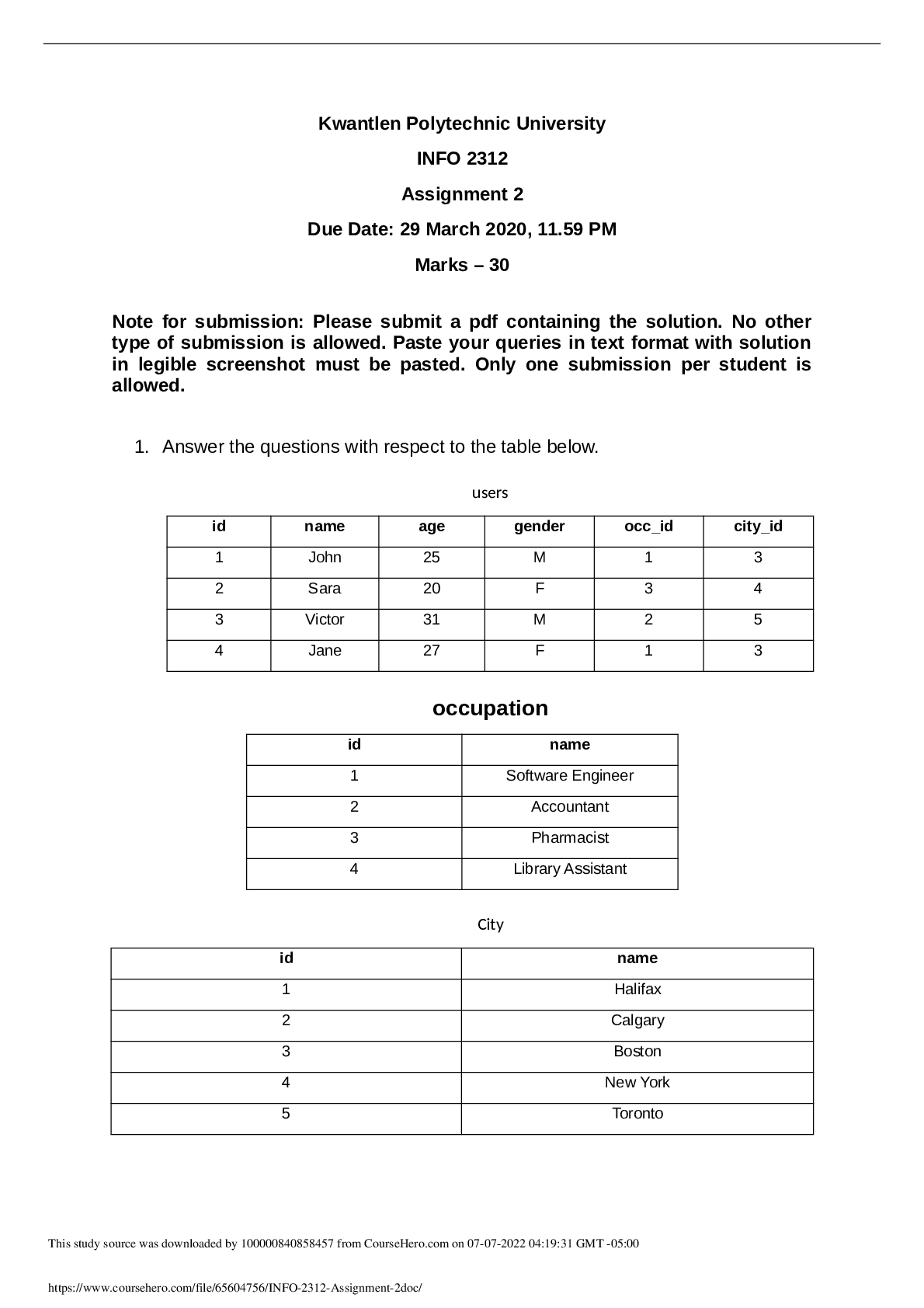
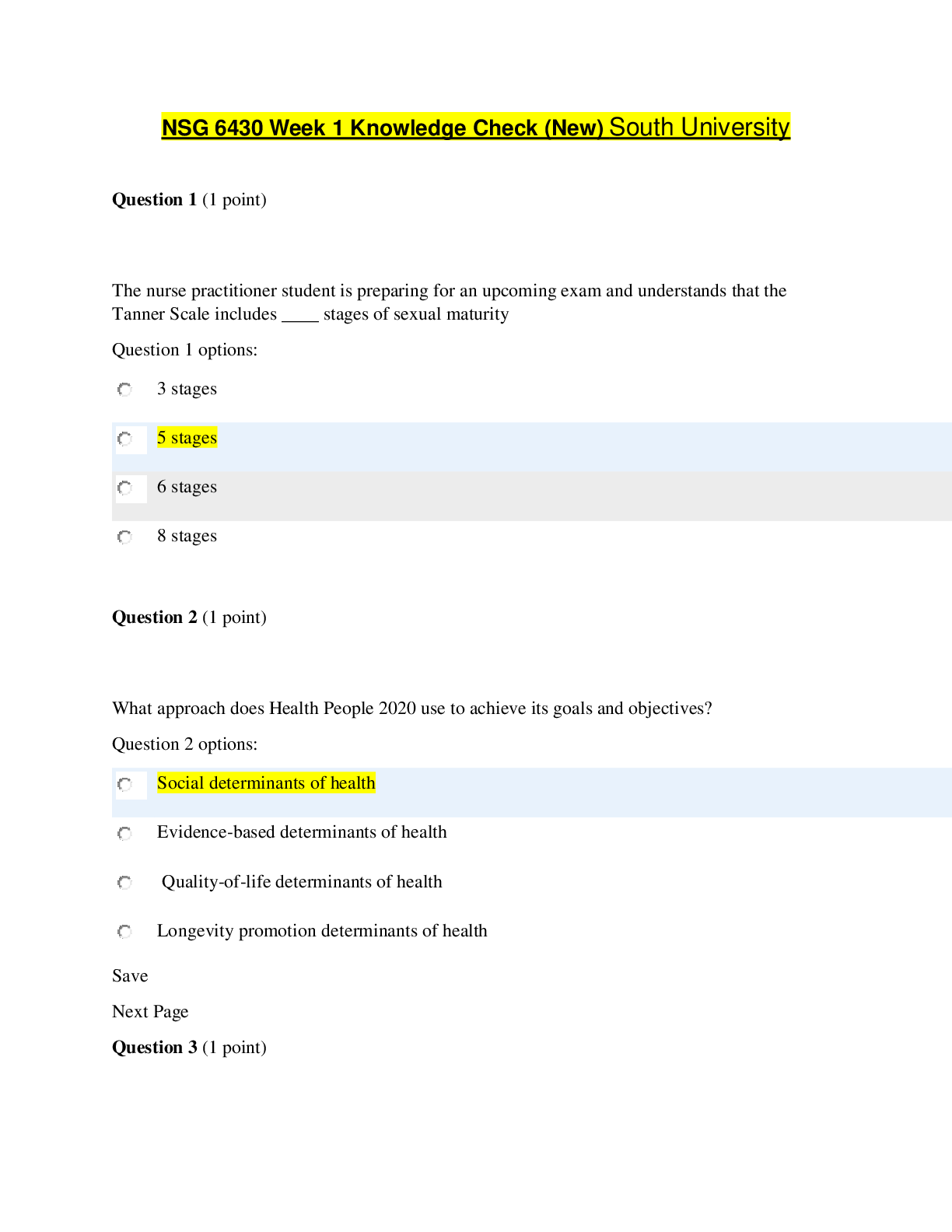
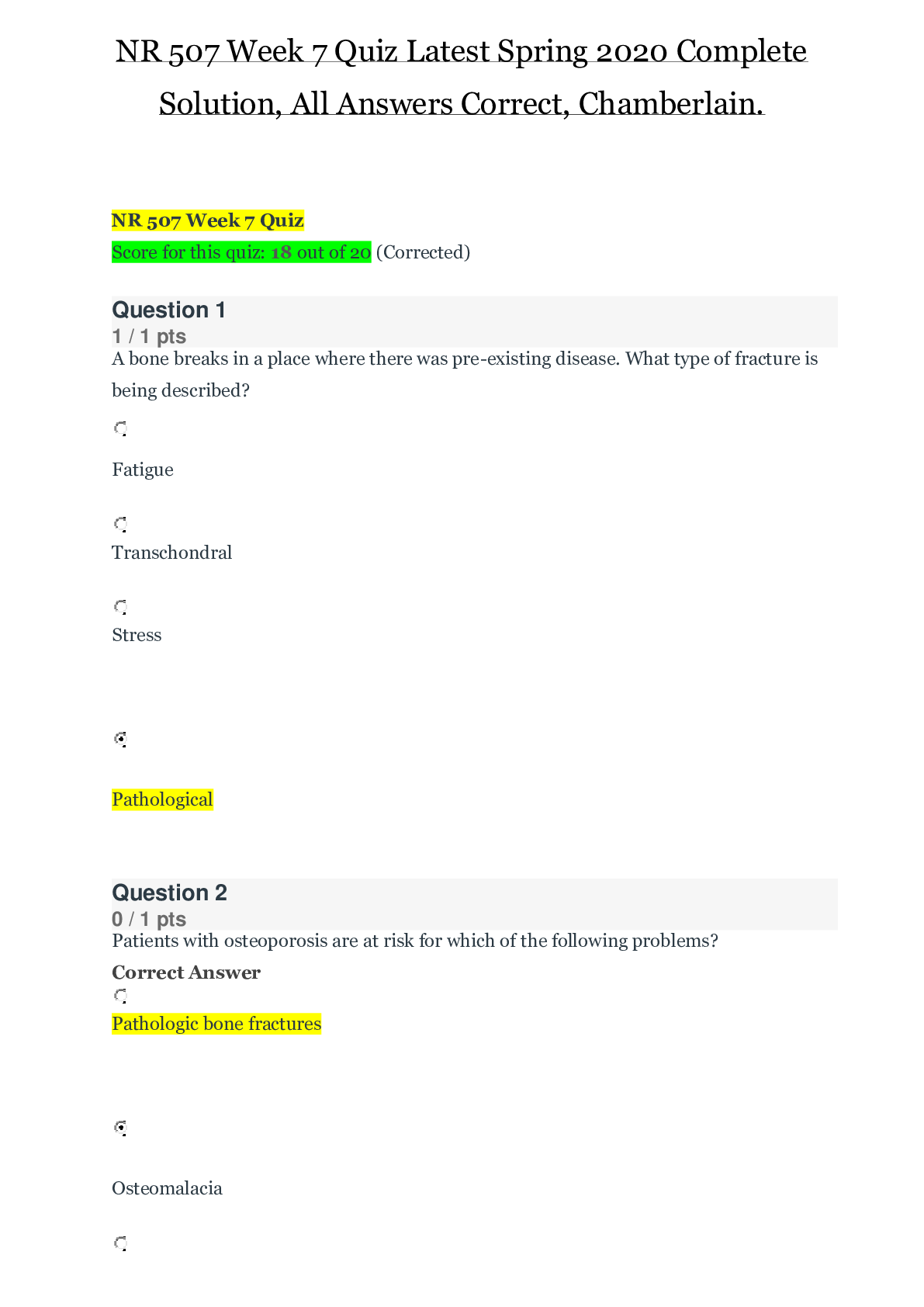
Self-Quiz Unit 5 Self-Quiz Unit 5 Question1 What property does the Fibonacci Sequence have? Not answered Marked out of Select one: 1.00 O a. It doubles in value every 5 numbers and then bec... omes infinite rather quickly. O b. At some point, it becomes 0 and then stops. O c. It adds the two previous numbers of a sequence together and continues forever. O d. It is undecided if the Fibonacci Sequence stops or not. O e. It multiplies the two previous values of a sequence with each other and continues forever. Your answer is incorrect. The correct answer is: It adds the two previous numbers of a sequence together, and continues forever. 0ia Question 2 Incorrect Mark 0.00 out of 1.00 Self-Quiz Unit 5 Let On = 2On- 1with starting values of a# = 1 . What is the solution to this recurrence relation? Select one: O a. It has no solution. b-o„ = ( 2;i. - l )2 c' On = 2’" 1 • d. a* = 2" X e-(ln = ))“ Your answer is incorrect. The correct answer is: an = 2"-1 Question 3 Not answered Marked out of 1.00 Let Fq = = — 2 and£]t = Fk_2 + for jfc > 2. Which one of the following is the value of F$ Select one: o a. 14 o b. 13 o c. 46 o d. -46 o e. 12 Your answer is incorrect. The correct answer is: 14Question 4 Incorrect Mark 0.00 out of 1.00 Let dk — 2dk-i 4- 3fc- with the starting value a\ = 5. What is the solution of this recurrence relation? Select one: O a. It has no solution. b. ak = + C- ak = 3*'+i + 2k+L • d. ak = 2(ft - l) + 3fcX e. ak = 2 (ft - 1) + 3k Your answer is incorrect. The correct answer is: ak = 3*"1"1 4- 2fc+1 Question 5 Correct Mark 1.00 out of 1.00 Consider the formula Ll ) 4- 1). What is the result? Select one: b-( L " ) - i c. n O / e .ft Your answer is correct. The correct answer is:Mark 0.00 out of 1.00 Question 6 Incorrect Let On = (in- 1 + n with a starting value of g.q = 4. What is the solution to this recurrence relation? Select one: O a. It has no solution. b.(h, = i + c-o„ = 2 + ^ ± ^ 2 0-an = i + fe-an = 4 4- n X Your answer is incorrect. The correct answer is: = 4 4- Question 7 Correct Mark 1.00 out of 1.00 Let (in = 4an-\_ — 4an- 2 with starting values of ci0 = 1 and q,\ = 2. What is the solution to this recurrence relation? Select one: O a. It has no solution. b-^ = {A n - l )2 c-On = An2 d an = n4 e. a*n = T V Your answer is correct. The correct answer is: an = 2nQuestion 8 If a recurrence relation S(k) has the characteristic equation Correct x2 -\- 2x — 8 = (z — 2)(x -\- 4), then which one of the following is the Mark 1.00 out of general solution. 1.00 Select one: a. a2k + fr( —4)^ / b. a(-2 )* + &4fc c-2fc-4fc d-a2k - b8k e-2ak - 4bk Your answer is correct. The correct answer is: a2k + &( — 4 )fc Question 9 Incorrect Mark 0.00 out of 1.00 Let ]In = 2//n_ i + 1 with rc > 1 and Hq = 0. What is the solution to this recursive equation? Select one: a. IIn = 2" - 1 b //n = 2fc c-Hn = 2° + l d. Hn — n2 + ftYour answer is incorrect. The correct answer is: Hn = 2" — 1Mark 0.00 out of 1.00 Question 10 Incorrect Which of the following is a closed-form expression for the solution of the recurrence B (0) = 1 , B(k) = B(k —1) + 4, k > 1? Select one: • a-B W = E ^ ( f l ( « ) + 4 ) X b. B(k) = + 1 c. B(k) = 2k + 1 d B(k) = 4* + 1 e-B(k) = 2 k Your answer is incorrect. The correct answer is: B(k) = 4k + 1MATH 1302 Discrete Mathematics - Term 2, 2018-2019 Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ► Self-Quiz Unit 5 Started on State Completed on Time taken Grade Sunday, 16 December 2018, 4:44 PM Finished Sunday, 16 December 2018, 5:48 PM 1 hour 3 mins 4.00 out of 10.00 (40%) Question 1 Let i?(0 ) = 0, # ( l ) = 1 and R(k) = 2R(k — 1) + R(k — 2) — 1for all incorrect k > 2. Which one of the following is the correct value of RiJj 'j? Mark 0.00 out of 1.00 Select one: O a. 5 O b. 9 • c. 4 X O d. 21 O e. 1 Your answer is incorrect. The correct answer is: 9Mark 1.00 out of 1.00 Question 2 Correct Your answer is correct. The correct answer is: 13 Question 3 Which one of the following is the characteristic polynomial of the Correct recurrence relation S(k) = 3S(k — 1 ) + 6S(k —2 ) — SS(k —3)? Mark 1.00 out of 1.00 Select one: a-XS + 3;t'2 + 6x —8 b- 3x2 -f Qx - 8 c-x 3 —3a;2 — 6a; 4- 8 V d. x4 - 3x3 + 6.T- - 8.t e-;r4 + - 6z 2 -f 82: Your answer is correct. The correct answer is: _ 3^ _ 6a; + 8Question4 Let T(0) = Oand Tin) = 1 4- T{\_nj2\ ) for n > 0. Which one of the Incorrect following is a solution for T(n) when n = 2WMark 0.00 out of 1.00 Select one: a. T(2m) = m 4- 1 b. T(2m) = m c. T(2m) = m — 1 d. T{2m) = 2m e. T(2m) = 2mX Your answer is incorrect. The correct answer is: T(2m) = m 4- 1 Question5 Incorrect Mark 0.00 out of 1.00 If a recurrence relation S(k) has the characteristic equation ■ ■- 1,. ■ 1 .' 1- then which one of the following is the correct form of the general solution of S(k'f? Select one: a- a3k + b3k b. a (-6 )k + b9k c. {a -f bk)(—3)kX d- a3k e (a -I- 6A’)3fc Your answer is incorrect. The correct answer is: (a -f bk)3kMark 0.00 out of 1.00 Question 6 Incorrect Question 7 Incorrect Mark 0.00 out of 1.00 What does "Recursion" mean? Select one: • a. Defining something recursive means it is infinite. X O b. The application of a function/definition to its own values. O c. Defining a function or set in such a way that it has finite and well defined values/elements. O d. Recursive functions usually produce an error, for example a division by zero. O e. Recursion means the result is always one. Your answer is incorrect. The correct answer is: The application of a function/definition to its own values. Which one of the following is a solution of the recurrence relation S(k) = 3S(k - 1) + 4 with 5 (1 ) = 1? Select one: a-S(k) = 5* — 4 b.S(k) = 6* - 5 c. S(k) = 2 k - 1 d.S{k) = k X e. S(k) =3* -2 Your answer is incorrect. The correct answer is: S(k) = 3* — 2Mark 0.00 out of 1.00 Question 8 Incorrect Question 9 Correct Mark 1.00 out of 1.00 Consider the sequence: 1,1,2,3,5,8,13,21,34,55,... What is the recurrence relation for this sequence? Select one: a- = &n—l + 2&n—2X k- (In = 2 + dn—2 c-&n — d„ —1 + dn—2 O d. It is a random sequence that has no recurrence relation. e-ftn = <4- 1 Your answer is incorrect. The correct answer is: a „ = a^ -i + &n-i What methods can you use to solve recurrence relations? Select one: O a. Solving Differential Equations. O b. Simplifying Binomials. • c. Iteration, Telescoping or finding Characteristic Roots. V O d. Multiplication and Division. O e. Logical Elimination. Your answer is correct. The correct answer is: Iteration, Telescoping or finding Characteristic Roots.Mark 1.00 out of 1.00 Question 10 Correct Let dk — 2dk-i + 3fc- with the starting value a\ = 5. What is the solution of this recurrence relation? Select one: O a. It has no solution. b. ak = + • c. ak - 3*+1 4- 2k+l / d. ak = 2(k - 1) + 3fc e. ak = 2 (k - 1) + 3k Your answer is correct. The correct answer is: ak = 3*"1"1 4- 2fc+1 https://my.uopeople.edu/mod/quiz/review.php?attempt=1567684 6/6MATH 1302 Discrete Mathematics - Term 2, 2018-2019 Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ► Self-Quiz Unit 5 Started on State Completed on Time taken Grade Sunday, 16 December 2018, 6:00 PM Finished Sunday, 16 December 2018, 6:06 PM 5 mins 43 secs 10.00 out of 10.00 (100%) Question 1 Consider the sequence: 1,1,2,3,5,8,13,21,34,55,... Correct What is the recurrence relation for this sequence? Mark 1.00 out of 1.00 Select one: a-&n — &n—1 + 2fln—2 k- (In — 2 0 n _l + f l „ - 2 c-&n = &n—1 “1“ &n— 2 O d. It is a random sequence that has no recurrence relation. e-^ = al_ i Your answer is correct. The correct answer is: an = + On-2Question2 Which one of the following is a solution of the recurrence relation Correct S(k) = 3S(k — 1 ) + 4 with 5 (1 ) = 1? Mark 1.00 out of 1.00 Select one: a.S(k) = 5* — 4 b. S(k) = S k - 5 c.S(k) = 2 k - 1 O Q_ ?? II e-S(k) = 3 k - 2 s/ Your answer is correct. The correct answer is: S(k) = 3k — 2 Question 3 Correct Mark 1.00 out of 1.00 Let On = — 4an_2 with starting values of ao = 1 and a\ = 2. What is the solution to this recurrence relation? Select one: O a. It has no solution. b. an = (An — l )2 c- an — An2 d On = n4 e.an = 2fl Your answer is correct. The correct answer is: an = 2nMark 1.00 out of 1.00 Question 4 Correct What methods can you use to solve recurrence relations? Select one: O a. Solving Differential Equations. O b. Simplifying Binomials. • c. Iteration, Telescoping or finding Characteristic Roots. V O d. Multiplication and Division. O e. Logical Elimination. Your answer is correct. The correct answer is: Iteration, Telescoping or finding Characteristic Roots. Question5 Let p(x) = ( ( ( r + 2)x — 1 )t ‘ + 3);t' -f 8. What is the value of p{ 1)? Correct Mark 1.00 out of Select one: 1.00 O a. 11 O b. -11 O c. 12 • d. 13 O e. -13 Your answer is correct. The correct answer is: 13Mark 1.00 out of 1.00 Question 6 Correct Question 7 Correct Mark 1.00 out of 1.00 Your answer is correct. The correct answer is: 9 Let On = dn-i + ti with a starting value of Oq = 4. What is the solution to this recurrence relation? Select one: O a. It has no solution. • b. O c. O d. O e. Your answer is correct. The correct answer is: n■fi — 4 4. 9Question8 Which one of the following is the characteristic polynomial of the Correct recurrence relation S(k) = 3S(k — 1) + GS(k —2) — SS(k —3)? Mark 1.00 out of 1.00 Select one: a- + 3a:2 + Go; — 8 b- 3a:2 -f Go' — 8 c-x :i — 3 r 2 — G r + 8 V d. -r4 - 3 r 1 + Gx2 - 8.t e-;r4 + 3a’3 - Go-2 + Sx Your answer is correct. The correct answer is: - 3 r 2 - 6x + 8 Question 9 Correct Mark 1.00 out of 1.00 Which of the following is a closed-form expression for the solution of the recurrence B (0) = 1, B(k) = B(k — 1) + 4, k > 1? Select one: a-B W = E l S 3 ( B ( n ) + 4) b.B{k) = + 1 s/ c. B(k) = 2Jfc + 1 d.B(k) = 4'l’ + 1 e-B(k) = 2k Your answer is correct. The correct answer is: B(k) = Ak + 1Question 10 Correct Let and for A’ > 2. Which one of the following is the value of F&? Mark 1.00 out of 1.00 Select one: • a. 14 O b. 13 O c. 46 O d. -46 O e. 12 Your answer is correct. The correct answer is: 14 https://my.uopeople.edu/mod/quiz/review.php?attempt=1567748 6/6MATH 1302 Discrete Mathematics - Term 2, 2018-2019 Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ► Self-Quiz Unit 5 Started on State Completed on Time taken Grade Sunday, 16 December 2018, 6:07 PM Finished Sunday, 16 December 2018, 6:11 PM 3 mins 38 secs 10.00 out of 10.00 (100%) Question 1 Let T ( 0) = 0 and T(n) = 1 -f T ( |_7i / 2j ) for n > 0. Which one of the Correct following is a solution for T (n ) when n = 2 m - Mark 1.00 out of 1.00 Select one: a. T(2m) = m + 1 sj b. T(2m) = 771 c. T(2m) — 771 — 1 d. T(2m) = 2m e. T(2m) = 2m Your answer is correct. The correct answer is: T(2m) = m -f 1Mark 1.00 out of 1.00 Question 2 Correct Question 3 Correct Mark 1.00 out of 1.00 What property does the Fibonacci Sequence have? Select one: O a. It doubles in value every 5 numbers and then becomes infinite rather quickly. O b. At some point it becomes 0 and then stops. • c. It adds the two previous numbers of a sequence together, and continues forever. ^ O d. It is undecided if the Fibonacci Sequence stops or not. O e. It multiplies the two previous values of a sequence with each other, and continues forever. Your answer is correct. The correct answer is: It adds the two previous numbers of a sequence together, and continues forever. If a recurrence relation S{k) has the characteristic equation ■ J J ■ i ■ J " . I i, then which one of the following is the general solution. Select one: a. a2k + & (-4 )fc / b. a(—2")k + b4k c-2k - 4fc d-£12* - b8k e-2ak - 4bk Your answer is correct. The correct answer is: a2k + b( —4)*Mark 1.00 out of 1.00 Question 4 Correct If a recurrence relation S(k) has the characteristic equation ■ J i,. ■ . .■■ then which one of the following is the correct form of the general solution of Si k)? Select one: a- a3k + b3k b.a (-G )k + bQk c. (a + bk)(—3)k d-a3k e.(a + bk) 3 * V Your answer is correct. The correct answer is: (a + bk) 3k Question 5 Correct Mark 1.00 out of 1.00 Consider the formula ( f: ^ 1). What is the result? Select one: ■>■(£ ) - 1 c. n • d-( ; ' V e .fe Your answer is correct. The correct answer is: (/: )Mark 1.00 out of 1.00 Question 6 Correct Let IIn = 2 J7 „_i + 1 with n > 1 and J70 = 0. What is the solution to this recursive equation? Select one: a. IIn = 2" - 1 V b Iln = 2fc c Hn = 2° + 1 d. / / n = ;j- -1- n e. //„ = 2" E ! ; = o " 2 Your answer is correct. The correct answer is: Hn = 2" — 1 Question 7 Correct Mark 1.00 out of 1.00 What does "Recursion" mean? Select one: O a. Defining something recursive means it is infinite. • b. The application of a function/definition to its own values. O c. Defining a function or set in such a way that it has finite and well defined values/elements. O d. Recursive functions usually produce an error, for example a division by zero. O e. Recursion means the result is always one. Your answer is correct. The correct answer is: The application of a function/definition to its own values.Mark 1.00 out of 1.00 Question 8 Correct Let On = 2On- 1with starting values of oq = 1 . What is the solution to this recurrence relation? Select one: O a. It has no solution. = (2n - 1 )- • c on = 2n_1/ d. On = T e- On = n 2 Your answer is correct. The correct answer is: an = 2"-1 Question 9 Correct Mark 1.00 out of 1.00 Let Fq = 6, F1 = —2 and Fk = F fc_2 + Fk_ 1for k > 2. Which one of the following is the value of F^? Select one: w a. 14 O b. 13 O c. 46 O d. -46 O e. 12 Your answer is correct. The correct answer is: 14Question 10 Correct What methods can you use to solve recurrence relations? Mark 1.00 out of 1.00 Select one: O a. Solving Differential Equations. O b. Simplifying Binomials. • c. Iteration, Telescoping or finding Characteristic Roots. V O d. Multiplication and Division. O e. Logical Elimination. Your answer is correct. Home ► My courses ► MATH 1302 - AY2019-T2 ► 13 December - 19 December ► Self-Quiz Unit 5 Started on State Completed on Time taken Grade Sunday, 16 December 2018, 6:12 PM Finished Sunday, 16 December 2018, 6:13 PM 1 min 30 secs 10.00 out of 10.00 (100%) Question 1 If a recurrence relation S(k) has the characteristic equation Correct x2 -f 2x — 8 = (;f — 2)(x -f 4), then which one of the following is the Mark 1.00 out of general solution. 1.00 Select one: a.a2k + & (-4 )fc / b-a(—2)k + b4k t-2 k - 4 k d-a2k - bSk e-2ak - 4bk Your answer is correct. The correct answer is: a2k + b(—4 )fcMark 1.00 out of 1.00 Question 2 Correct Leti^(O) = 0, /£ (!) = 1 and R(k) = 2R(k — 1) + R(k — 2) — 1for all k > 2. Which one of the following is the correct value of R(5)? Select one: o a. 5 ® b. 9 o c. 4 o d. 21 o e. 1 Your answer is correct. The correct answer is: 9 Question 3 Correct Mark 1.00 out of 1.00 Which of the following is a closed-form expression for the solution of the recurrence B (0) = 1 , B(k) = B(k — 1) + 4, k > 1? Select one: a-- B W = E ^ ( £ W + 4) b. B{k) = + 1 s/ c. B(k) = 2Jfc + 1 d. B(k) = 4,L’ + 1 e-B(k) = 2k Your answer is correct. The correct answer is: B(k) = Ak + 1Mark 1.00 out of 1.00 Question 4 Correct Question 5 Correct Mark 1.00 out of 1.00 What does "Recursion" mean? Select one: O a. Defining something recursive means it is infinite. • b. The application of a function/definition to its own values. O c. Defining a function or set in such a way that it has finite and well defined values/elements. O d. Recursive functions usually produce an error, for example a division by zero. O e. Recursion means the result is always one. Your answer is correct. The correct answer is: The application of a function/definition to its own values. Let T (0 ) = 0 and T(n) = 1 -f T{ \_nj2J ) for n > 0. Which one of the following is a solution for 7 ( j when n = 2m. Select one: a. T(2m) = m -fi 1 / b. T(2m) = m c. T(2m) — m — 1 d. T(2m) = 2m e. T(2m) = 2m Your answer is correct. The correct answer is: T(2m) = m -f 1Mark 1.00 out of 1.00 Question 6 Correct Let On = 4dfl_ i — 4an_2 with starting values of r(0 = 1 and a\ = 2. What is the solution to this recurrence relation? Select one: O a. It has no solution. b-On = (4n - 1)- c On = Art2 d On = n4 e.a^ = T V Your answer is correct. The correct answer is: an = 2n Question 7 Correct Mark 1.00 out of 1.00 Consider the formula ( '' 1) + ( . 1). What is the result? Select one: ■•(£=?) •>■(£ ) - 1 c. n e-k Your answer is correct. The correct answer is:Mark 1.00 out of 1.00 Question 8 Correct Your answer is correct. The correct answer is: 13 Question 9 Which one of the following is the characteristic polynomial of the Correct recurrence relation S(k) = 3S(k — 1 ) + 6S(k —2 ) — SS(k —3)? Mark 1.00 out of 1.00 Select one: a-XS + 3;t'2+ 6x —8 b- 3x2 -f 6x - 8 c-x 3 —3:r2 — 6:r 4- 8 V d. ;r 4 - 3 x 3 + 6 .T - - 8.t e-;r4 + 3x 'J - 6.t- + Sx Your answer is correct. The correct answer is: _ 3r 2 _ + gMark 1.00 out of 1.00 Question 10 Correct • c. It adds the two previous numbers of a sequence together, and continues forever. ^ O d. It is undecided if the Fibonacci Sequence stops or not. O e. It multiplies the two previous values of a sequence with each other, and continues forever. Your answer is correct. The correct answer is: It adds the two previous numbers of a sequence together, and continues forever. What property does the Fibonacci Sequence have? Select one: O a. It doubles in value every 5 numbers and then becomes infinite rather quickly. O b. At some point it becomes 0 and then stops. https://my.uopeople.edu/mod/quiz/review.php?attempt=1567768 6/6 [Show More]

Last updated: 1 year ago

Preview 1 out of 30 pages