CSE 6140: Final Practice Questions - Georgia Institute Of Technology CSE 6140

Document Content and Description Below

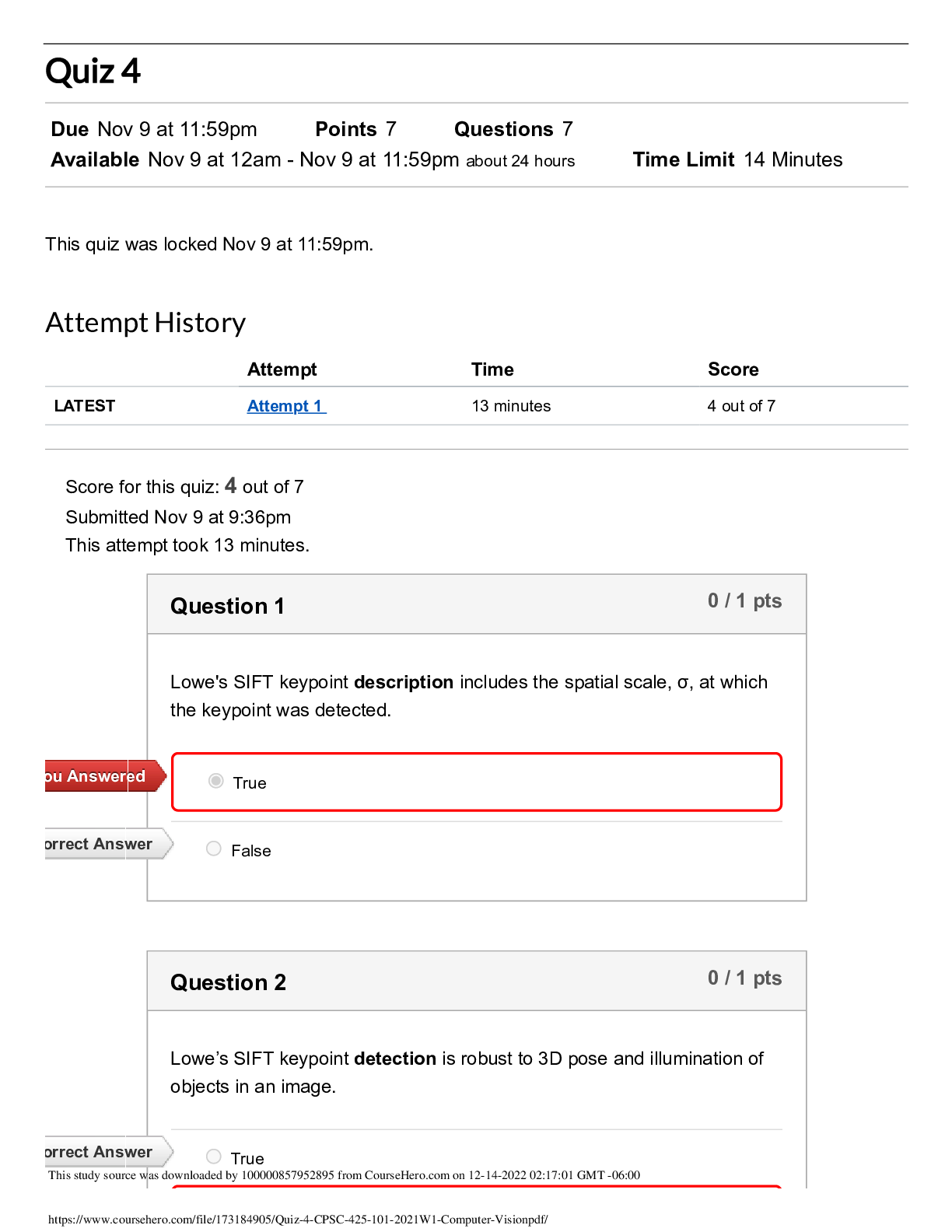
CSE 6140: Final Practice Questions INSTRUCTIONS: Remember a subset of these problems will appear on the Final. Hence the Honor Code for exams applies here. You are only allowed to use resources use... d in the course such as the two textbooks and the lecture slides. No collaboration or Web Searching is allowed. 1 Greedy 1: Schedule with Preferred Finished Time We have a scheduling problem with n jobs, where each job i has a length li and a preferred finish time fi , and we must schedule all the jobs on a single machine without overlaps between jobs. Given a schedule, let us denote the completion time of job i by Ci . If Ci is before the preferred time fi , we get a reward equal to the time we have saved. If we complete the job after the preferred time, we pay a penalty equal to the amount of time that we are late. Our total reward (which we want to maximize) is the sum of all rewards for early completion minus the sum of all penalties for late completion. Note that here we have a scheduling problem slightly different from the others we have seen in class. (a) Argue carefully that there is an optimal schedule that has no idle time (actually, we want to argue that every optimal schedule has no idle time). That is, every optimal schedule always has one job start at the same time the previous job finishes. (Hint: Show how to change any schedule with idle time to another schedule that has no idle time and gets at least more reward.) (b) Consider the greedy algorithm where we sort the jobs by length and schedule them in that order, shortest job first, with no idle time. Prove that this achieves a net reward at least as great as that of any schedule. (Note: In lecture we proved that a different greedy algorithm is optimal for a different goal, that of minimizing the maximum lateness. You cannot simply quote that result because it does not apply to this algorithm or to these rewards and penalties. But a similar exchange argument will work in this new case.) 1 2 Greedy 2: Classroom Scheduling Consider the following scheduling problem that concerns finding an assignment of rooms to classes. INPUT: A set of classes specified as a set S = {(xi , yi), 1 ≤ i ≤ n} of time intervals. Think of interval (xi , yi) as being a request for a room for a class that meets from time xi to time yi . OUTPUT: Find an assignment of classes to rooms that uses the fewest number of rooms. Note that every room request must be honored and that no two classes can use a room at the same time. (a) Consider the following iterative algorithm. Assign as many classes as possible to the first room (we can do this using the greedy algorithm discussed in class for activity scheduling), then assign as many classes as possible to the second room, then assign as many classes as possible to the third room, etc. Does this algorithm solve the Classroom Scheduling Problem? Justify your answer. (b) Consider the following algorithm. Process the classes in increasing order of start times. Assume that you are processing class C. If there is a room R such that R has been assigned to an earlier class, and C can be assigned to R without overlapping previously assigned classes, then assign C to R. Otherwise, put C in a new room. Does this algorithm solve the Classroom Scheduling Problem? Justify your answer. HINT: Let s be the maximum number of intervals that overlap at one particular point in time. Obviously, you need at least s rooms. Therefore any algorithm that uses only s rooms is obviously optimal. This lower bound on the number of rooms required allows you to prove optimality without using an exchange argument. Show that the correct greedy strategy generates a schedule that uses exactly s rooms. 3 DP 1: ADJACENT-PAIR-PRODUCT-SUM Given a list of n integers, v1, ..., vn, find the largest ADJACENT-PAIRPRODUCT-SUM, which is the largest sum that can be formed by multiplying adjacent elements in the list. Each element can be matched with at most one of its neighbors (but is also allowed to be left alone). For exam2 ple, given the list 1, 2, 3, 1 the largest ADJACENT-PAIR-PRODUCT-SUM is 8 = 1 + (2 × 3) + 1, and given the list 2, 2, 1, 3, 2, 1, 2, 2, 1, 2 the largest ADJACENT-PAIR-PRODUCT-SUM is 19 = (2 × 2) + 1 + (3 × 2) + 1 + (2 × 2) + 1 + 2. Another ADJACENT [Show More]

Last updated: 1 year ago

Preview 1 out of 8 pages