Applied Probability and Statistics WGU C955, Top Exam Questions and answers, graded A+, latest version

Document Content and Description Below

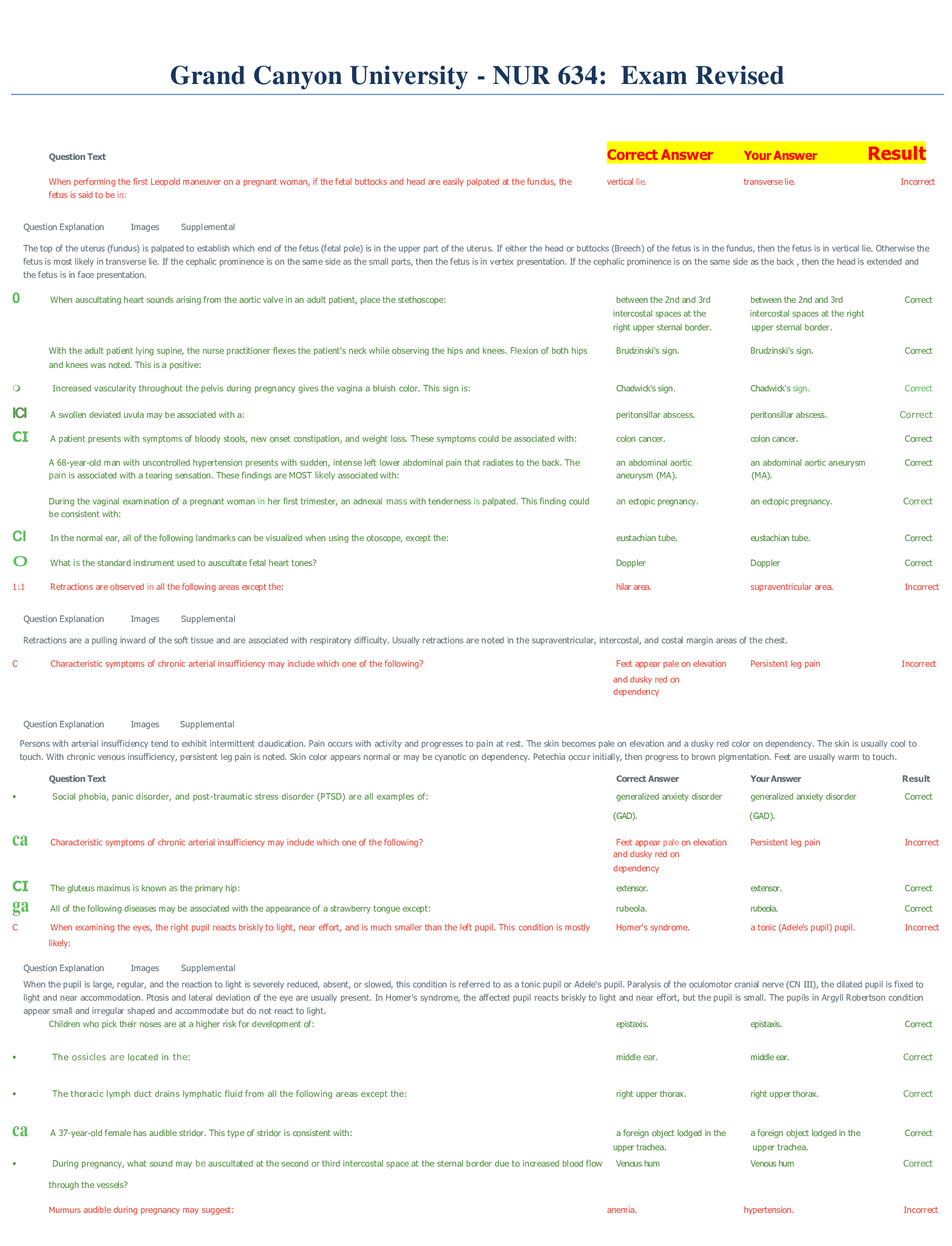
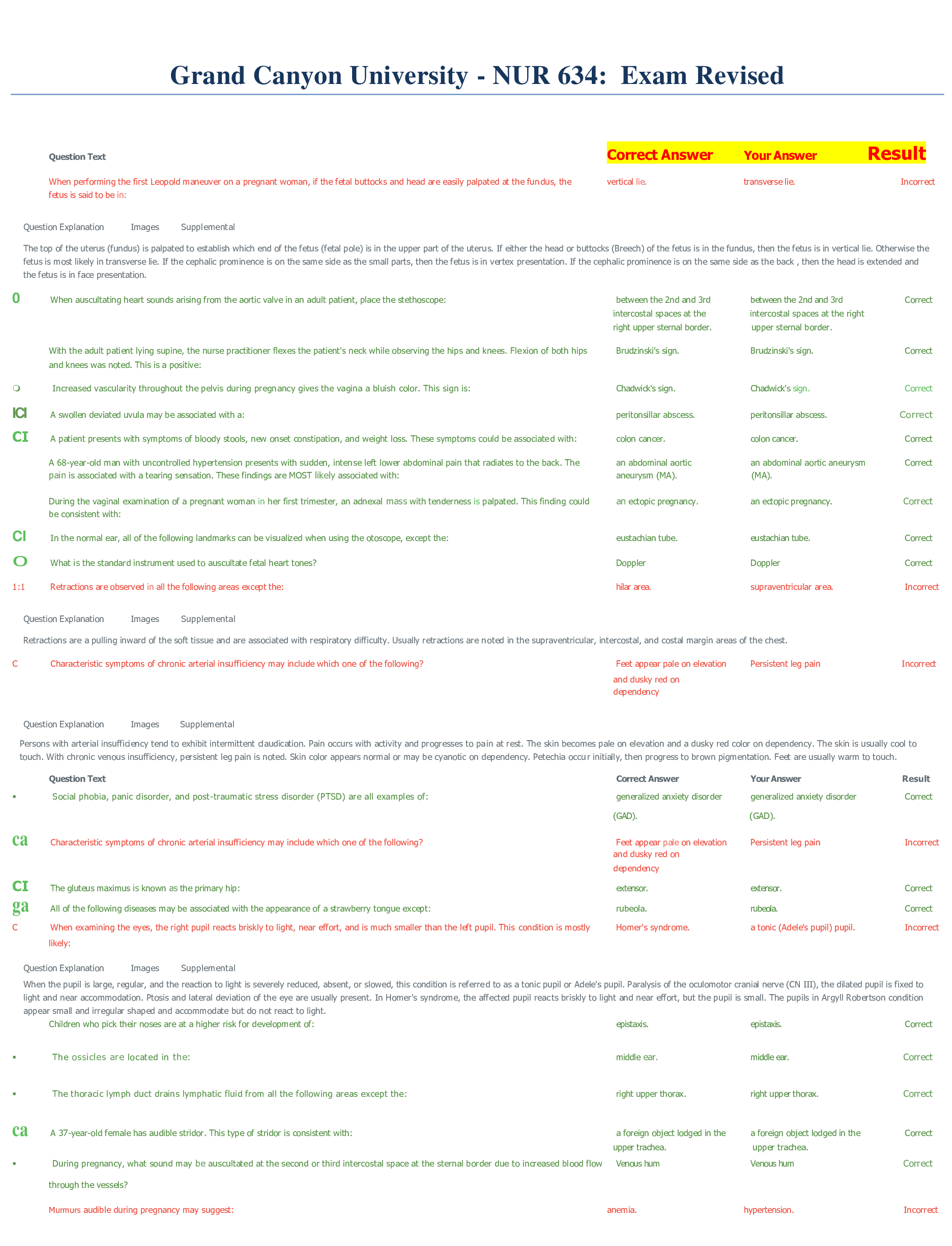
Applied Probability and Statistics WGU C955, Top Exam Questions and answers, graded A+, latest version Changing Improper Fractions and Mixed Numbers - ✔✔-Improper fractions can be converted t... o mixed numbers by following these steps: Write division problem with numerator divided by denominator. Divide to determine quotient and remainder. Write mixed number with the quotient as the whole number and the remainder as the numerator over the same denominator. Changing Mixed Numbers Into Improper Fractions - ✔✔-Mixed numbers can also be converted to improper fractions by following these steps: Multiply the whole number by the denominator of the fraction. To the product given by step 1, add the number of the numerator. Write the result of step 2 as the numerator of the improper fraction. The denominator of the improper fraction should be the denominator of the original fraction. Simplify the improper fraction by diving the numerator and denominator by all common factors. Discrete Data - ✔✔-Has distinct values, can be counted, has unconnected points (dots) Continuous data - ✔✔-Has values within a range, measured (not counted) does not have gaps between data points. (connected lines or curves) Sign rule for Multiplication and division - ✔✔-1. +# x +# = +# 2. -# x -# = +# A product or division of two numbers of the same sign will result in a positive number 3. -# x +# = -# 4. +# x -# = -# A product or division of two numbers of different signs will result in a negative number Prime Number - ✔✔-A prime number is a number that has exactly two positive factors; 1 and itself. Composite Number - ✔✔-A number that is not prime. It has 2 or more positive factor, including 1 and itself. Prime Factorization - ✔✔-Writing the number as a product of only prime numbers. Greatest Common Factor (GCF) - ✔✔-The larges number that divides all the given numbers evenly. Multiples of a number - ✔✔-Numbers that can be obtained by multiplying the given number by 1, 2, 3, 4, etc. Least Common Multiple (LCM) - ✔✔-the smallest positive number that can be divided by the given numbers Centigrade/Fahrenheit Conversions - ✔✔-C = (F - 32) X 5/9 F = (C X 9/5) + 32 Unit Conversions for Household Measures of Volume - ✔✔-1 tablespoon = 3 teaspoons 1 oz = 2 tablespoons 1 cup = 8 oz 1 pint = 2 cups 1 quart = 1 pints 1 gallon = 4 quarts Common Metric Conversions - ✔✔-1 L = 1000 mL 1kg = 1000 g 1 g = 1000 mg 1 mg = 1000 mcg Conversions between Household and Metric Units - ✔✔-1 cc (Cubic Centimeter) = 1 mL 1 oz = 30 mL 1 L = 1.057 qt 1 tsp = 5 mL 1 kg = 2.2 lbs 1 oz = 28.35 g Like Terms - ✔✔-Terms that have the same variable raised to the same power; they can be combined using addition and subtraction Addition/Subtraction Principle - ✔✔-We can add or subtract the same number to both sides of an equation and the resulting expression remains equal. Multiplication/Division Principle - ✔✔-We can multiply or divide the same number to both sides of an equation and the resulting expression remains equal. (Divide by 0 is not allowed) Butterfly Method - ✔✔-Cross Multiply, if a/b = c/d then a x d = b x c Slope-Intercept Equation - ✔✔-y = mx + b Where "m" is the slope, "b" is the y-intercept, and "x" and "y" follow the coordinate formula (x,y) Slope of a line - ✔✔-The slope of a line is the ratio of the vertical change between two points on the line to the horizontal change between those two points. rise: (y2 - y1) / run: (x2 - x1) Reducing Fractions Using Prime Factorization - ✔✔-The steps to reduce a fraction through prime factorization are as follows: List the prime factors of both the numerator and denominator. Cancel the factors that are common to both the numerator and denominator. Multiply across the numerator and denominator. 6/8 6/8 = 2x3/2x2x2x 2x3/2x2x2x = 3/2x2 3/2x2 = 3/4 Reducing Fractions Using Common Factors - ✔✔-The steps for the common factors method are as follows: Divide numerator and denominator by a common factor. Continue to divide by common factors. Write the reduced factor. -28/42 -28/42 = (-28/7) / (42/7) = -4/6 Reduce -4/6 = (-4/2)/(6/2) = -2/3 Least Common Denominator - ✔✔-The least common multiple of the denominators of two or more fractions. Let's determine the least common denominator of 13 and −27. Ask "do 3 and 7 have a factor in common?" No. So, this is situation 1. Multiply 3×7=21. 21 is the least common multiple of the numbers 3 and 7, therefore it is the least common denominator for 13 and −27. 21 is the LCD for 13 and −27 Transforming Fractions - ✔✔-Divide the least common denominator by the current denominator. Multiply both the numerator and the denominator by this integer. Let's now transform 1/3 and −2/7 each into their equivalent fractions that share a common denominator of 21 , which we found in the example above. First, convert 1/3 to an equivalent fraction with a denominator of 21 . Divide the LCD (the new denominator) by the current denominator. 21÷3=7 Multiply the numerator and denominators by 7 . (1×7)/(3×7)=721 Adding Fractions with the Same Denominator - ✔✔-Add or subtract the numerators of all the fractions in the expression Keep the same denominator! (The temptation to add the two denominators is very strong—resist.) If necessary, reduce the answer. Adding Fractions with Different Denominators - ✔✔-Find the least common denominator (LCD). Use the LCD to find the equivalent fractions and rewrite the expression. Add or subtract the numerators of all the fractions in the expression. Keep the denominator the same—do not add them. If necessary, reduce the answer. Adding and Subtracting Mixed Number Fractions - ✔✔-Change the mixed numbers* to improper fractions*. Find the least common denominator (LCD) if the fractions have different denominators and convert to equivalent fractions with the LCD. Add or subtract the numerators of all the fractions in the expression. Keep the denominator the same. Change improper fractions to a mixed number (if needed). If necessary, reduce the fraction to lowest form. Subtract the following mixed numbers: 8 5/6 − 5 1/2 Step 1: Change the mixed number to an improper fraction. 8 5/6 = 53/6 and 5 1/2=11/2 Step 2: Find equivalent fractions with the least common multiple. Convert the fractions to equivalent fractions with the LCM. The least common multiple is 6 , therefore: 53/6 does not need to change Multiply the numerator and denominator of 11/2 by 3 53/6 − 11/2 = 53/6 − 33/6 Step 3: Subtract like fractions. [Show More]

Last updated: 1 year ago

Preview 1 out of 21 pages