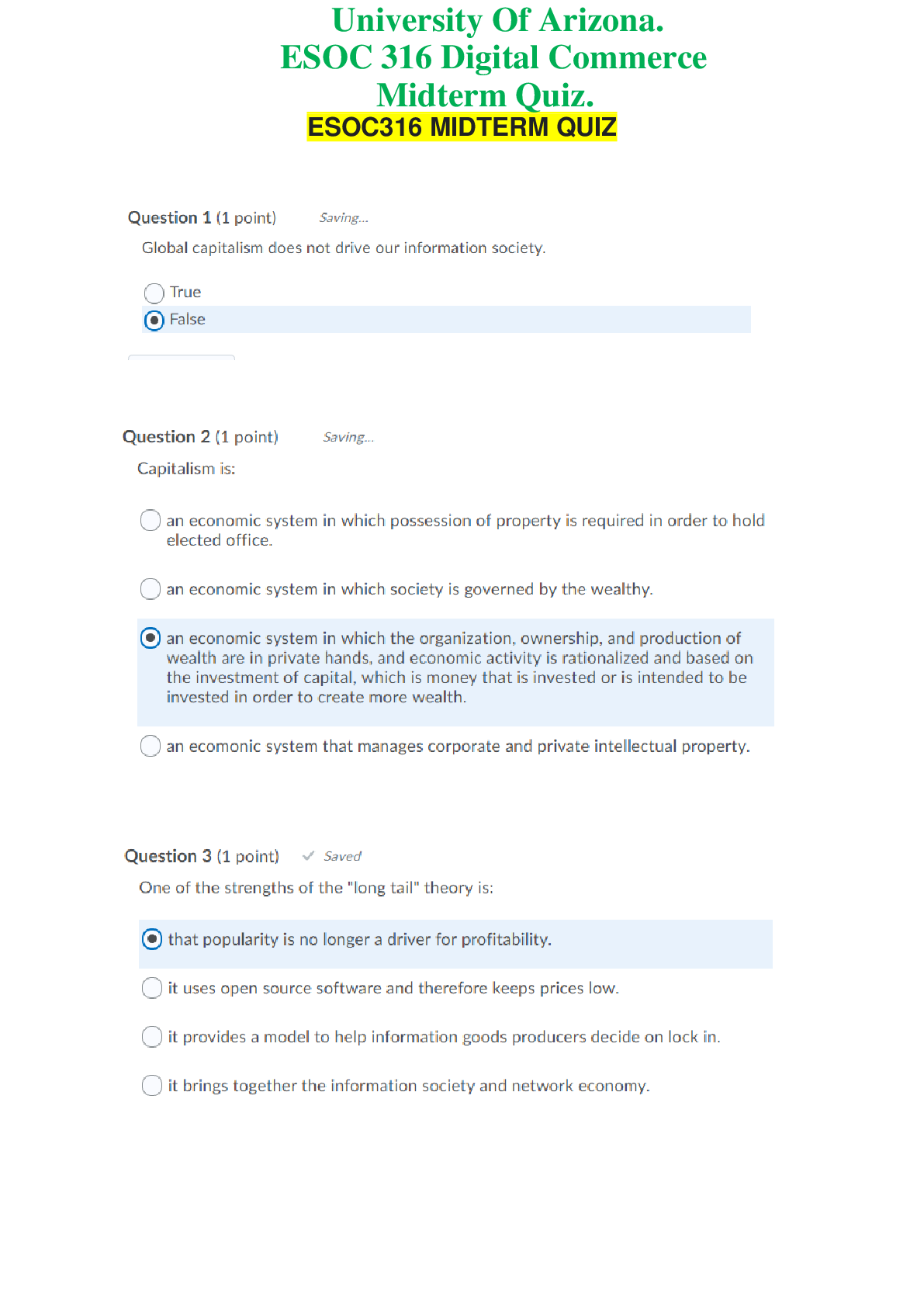
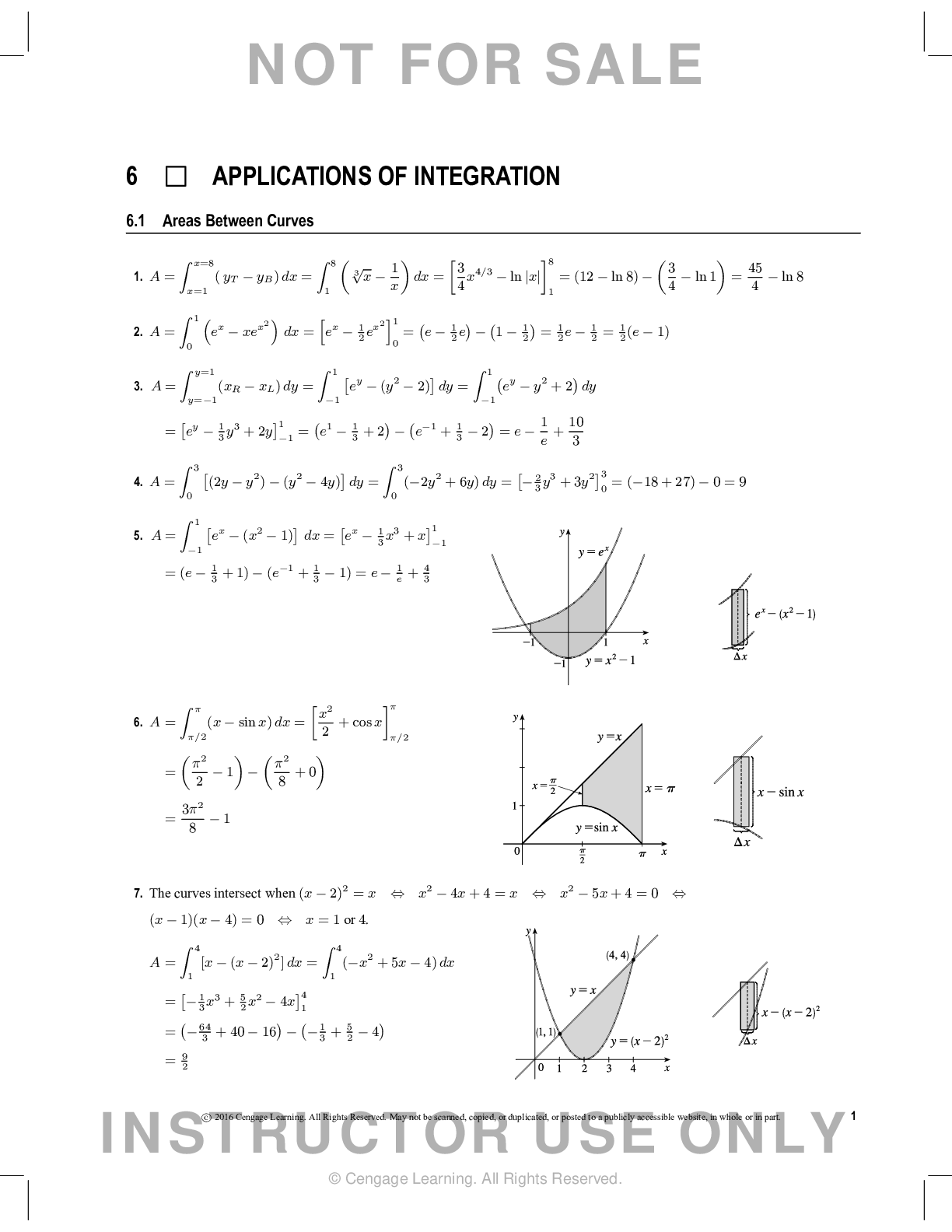
Calculus > QUESTIONS & ANSWERS > Chapter 8 FURTHER APPLICATIONS OF INTEGRATION. Work and Answers (All)
Chapter 8 FURTHER APPLICATIONS OF INTEGRATION. Work and Answers
Document Content and Description Below
8.1 Arc Length 1. = 2 − 5 ⇒ = −31 1 + ()2 = −31 1 + (2)2 = √5 [3 − (−1)] = 4√5. The arc length can be calculated using the distanc... e formula, since the curve is a line segment, so = [distance from (−1 −7) to (31)] = [3 − (−1)]2 + [1 − (−7)]2 = √80 = 4√5 2. Using the arc length formula with = √2 − 2 ⇒ = − √2 − 2 , we get = 01 1 + 2 = 01 1 + 2 −22 = 01 √√22−2 = √201 √2 2 − 2 = √2sin−1√21 0 = √2sin−1√12 − sin−1 0 = √2 4 − 0 = √2 4 The curve is a one-eighth of a circle with radius √2, so the length of the arc is 1 8 2 · √2 = √2 4 , as above. 3. = sin ⇒ = cos ⇒ 1 + ()2 = 1 + cos2. So = 0 √1 + cos2 ≈ 38202. 4. = − ⇒ = (−−) + −(1) = −(1 − ) ⇒ 1 + ()2 = 1 + [−(1 − )]2. So = 02 1 + −2(1 − )2 ≈ 21024. 5. = − ln ⇒ = 1 − 1 ⇒ 1 + ()2 = 1 + (1 − 1)2. So = 14 1 + (1 − 1)2 ≈ 34467. 6. = 2 − 2 ⇒ = 2 − 2 ⇒ 1 + ()2 = 1 + (2 − 2)2. So = 02 1 + (2 − 2)2 ≈ 29579. 7. = √ − ⇒ = 12√ − 1 ⇒ 1 + ()2 = 1 + 2√1 − 12. So = 14 1 + 2√1 − 12 ≈ 36095. 8. 2 = ln ⇔ = 2 ⇒ = 22 ⇒ 1 + ()2 = 1 + 4222. So = −11 1 + 4222 ≈ 42552. 9. = 1 + 632 ⇒ = 912 ⇒ 1 + ()2 = 1 + 81. So = 01 √1 + 81 = 182 12 81 1 = 1 + 81 = 81 , = 81 1 · 2 3 3282 1 = 243 2 82√82 − 1 10. 362 = (2 − 4)3, ≥ 0 ⇒ = 1 6(2 − 4)32 ⇒ = 1 6 · 3 2(2 − 4)12(2) = 1 2 (2 − 4)12 ⇒ 1 + ()2 = 1 + 1 4 2(2 − 4) = 1 4 4 − 2 + 1 = 1 4(4 − 42 + 4) = 1 2(2 − 2)2. So = 23 1 2(2 − 2)2 = 23 1 2(2 − 2) = 1 2 1 3 3 − 23 2 = 1 2 (9 − 6) − 8 3 − 4 = 1 2 13 3 = 13 6 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 1 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.2 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 11. = 3 3 + 1 4 ⇒ 0 = 2 − 412 ⇒ 1 + (0)2 = 1 + 4 − 1 2 + 1614 = 4 + 12 + 1614 = 2 + 412 2. So = 12 1 + (0)2 = 12 2 + 412 = 12 2 + 412 = 1 33 − 412 1 = 8 3 − 18 − 1 3 − 1 4 = 73 + 1 8 = 59 24 12. = 4 8 + 1 42 ⇒ = 1 2 3 − 1 2 −3 ⇒ 1 + ()2 = 1 + 1 4 6 − 1 2 + 1 4−6 = 1 4 6 + 1 2 + 1 4 −6 = 1 2 3 + 1 2 −32. So = 12 1 23 + 1 2 −32 = 12 1 2 3 + 1 2 −3 = 1 8 4 − 1 4 −22 1 = 2 − 16 1 − 1 8 − 1 4 = 2 + 1 16 = 33 16 . 13. = 1 3√ ( − 3) = 1 3 32 − 12 ⇒ = 1 2 12 − 1 2 −12 ⇒ 1 + ()2 = 1 + 1 4 − 1 2 + 1 4 −1 = 1 4 + 1 2 + 1 4 −1 = 1 2 12 + 1 2 −122. So = 19 1 2 12 + 1 2−12 = 1 2 2 3 32 + 2129 1 = 1 2 2 3 · 27 + 2 · 3 − 2 3 · 1 + 2 · 1 = 1 2 24 − 8 3 = 1 2 64 3 = 32 3 . 14. = ln(cos) ⇒ = −tan ⇒ 1 + ()2 = 1 + tan2 = sec2 . So = 03 √sec2 = 03 sec = ln|sec + tan| 0 3 = ln2 + √3 − ln(1 + 0) = ln2 + √3. 15. = ln(sec) ⇒ = sec tan sec = tan ⇒ 1 + 2 = 1 + tan2 = sec2 , so = 04 √sec2 = 04 |sec| = 04 sec = ln(sec + tan) 0 4 = ln√2 + 1 − ln(1 + 0) = ln√2 + 1 16. = 3 + 1 2 cosh 2 ⇒ 0 = sinh 2 ⇒ 1 + ()2 = 1 + sinh2(2) = cosh2(2). So = 01 cosh2(2) = 01 cosh 2 = 1 2 sinh 21 0 = 1 2 sinh 2 − 0 = 1 2 sinh 2. 17. = 1 42 − 1 2 ln ⇒ 0 = 12 − 21 ⇒ 1 + (0)2 = 1 + 1 42 − 12 + 412 = 142 + 1 2 + 412 = 1 2 + 212. So = 12 1 + (0)2 = 12 12 + 21 = 12 1 2 + 21 = 412 + 1 2 ln||2 1 = 1 + 1 2 ln 2 − 1 4 + 0 = 34 + 12 ln 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.1 ARC LENGTH ¤ 3 18. = √ − 2 + sin−1√ ⇒ = 2√1 − −22 + 2√ √11 − = 2√2−√21− = 1 − ⇒ 1 + 2 = 1 + 1 − = 1. The curve has endpoints (00) and 1 2 , so = 01 1 = lim →0+ 1 1 = lim →0+ 2√ 1 = lim →0+ 2√1 − 2√ = 2 − 0 = 2. 19. = ln(1 − 2) ⇒ 0 = 1 1 − 2 · (−2) ⇒ 1 + 2 = 1 + (1 −422)2 = 1 − 2(1 2−+24)2+ 42 = 1 + 2 (1 −22+)24 = (1 + (1 − 2 2) )2 2 ⇒ 1 + 2 = 1 + 1 − 2 2 2 = 1 + 1 − 2 2 = −1 + 1 −22 [by division] = −1 + 1 +1 + 1 −1 [partial fractions]. So = 012 −1 + 1 +1 + 1 −1 = − + ln|1 + | − ln|1 − | 1 02 = − 1 2 + ln 3 2 − ln 1 2 − 0 = ln 3 − 1 2 . 20. = 1 − − ⇒ 0 = −(−−) = − ⇒ 1 + ()2 = 1 + −2. So = 02 1 + −2 = 1−2 1 + 2 −1 [ = −] 23 = ln 1 + √1 + 2 − √1 + 2 1−2 [or substitute = tan ] = ln 1 + √1 + −4 −2 − √1 + −4 − ln 1 + √2 1 + √2 = ln1 + √1 + −4 − ln−2 − √1 + −4 − ln1 + √2 + √2 = ln1 + √1 + −4 + 2 − √1 + −4 − ln1 + √2 + √2 21. = 1 2 2 ⇒ = ⇒ 1 + ()2 = 1 + 2. So = −11 √1 + 2 = 201 √1 + 2 [by symmetry] 21 = 2 2 √1 + 2 + 1 2 ln + √1 + 2 1 0 or substitute = tan = 2 1 2 √2 + 1 2 ln1 + √2 − 0 + 1 2 ln 1 = √2 + ln1 + √2 22. 2 = ( − 4)3 ⇒ = ( − 4)32 [for 0] ⇒ = 3 2( − 4)12 ⇒ 1 + ()2 = 1 + 9 4( − 4) = 9 4 − 8. So = 58 9 4 − 8 = 1310 4 √ 4 9 ==9 49 4 − 8, = 4 9 2 3 3210 134 = 8 271032 − 13 4 32 or 27 1 80√10 − 13√13 23. From the figure, the length of the curve is slightly larger than the hypotenuse of the triangle formed by the points (12), (112), and (212). This length is about √102 + 12 ≈ 10, so we might estimate the length to be 10. = 2 + 3 ⇒ 0 = 2 + 32 ⇒ 1 + (0)2 = 1 + (2 + 32)2. So = 12 1 + (2 + 32)2 ≈ 100556. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.4 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 24. From the figure, the length of the curve is slightly larger than the hypotenuse of the triangle formed by the points (11), 2 1, and 2 2 . This length is about 2 2 + 2 − 12 ≈ 17, so we might estimate the length to be 17. = + cos ⇒ 0 = 1 − sin ⇒ 1 + (0)2 = 1 + (1 − sin)2. So = 02 1 + (1 − sin)2 ≈ 17294. 25. = sin ⇒ = cos + (sin)(1) ⇒ 1 + ()2 = 1 + (cos + sin)2. Let () = 1 + ()2 = 1 + (cos + sin)2. Then = 02 (). Since = 10, ∆ = 210 − 0 = 5 . Now ≈ 10 = 35 (0) + 4 5 + 2 25 + 4 35 + 2 45 + 4 55 + 2 65 + 4 75 + 2 85 + 4 95 + (2) ≈ 15498085 The value of the integral produced by a calculator is 15374568 (to six decimal places). 26. = √3 ⇒ = 1 3−23 ⇒ = 16 (), where () = 1 + 1 9−43. Since = 10, ∆ = 610 − 1 = 1 2. Now ≈ 10 = 132[(1) + 4(15) + 2(2) + 4(25) + 2(3) + 4(35) + 2(4) + 4(45) + 2(5) + 4(55) + (6)] ≈ 5074212 The value of the integral produced by a calculator is 5074094 (to six decimal places). 27. = ln(1 + 3) ⇒ = 1 1 + 3 · 32 ⇒ = 05 (), where () = 1 + 94(1 + 3)2. Since = 10, ∆ = 510 − 0 = 1 2. Now ≈ 10 = 132[(0) + 4(05) + 2(1) + 4(15) + 2(2) + 4(25) + 2(3) + 4(35) + 2(4) + 4(45) + (5)] ≈ 7094570 The value of the integral produced by a calculator is 7118819 (to six decimal places). 28. = −2 ⇒ = −2(−2) ⇒ = 02 (), where () = 1 + 42−22. Since = 10, ∆ = 210 − 0 = 1 5. Now ≈ 10 = 15 3 [(0) + 4(02) + 2(04) + 4(06) + 2(08) + 4(1) + 2(12) + 4(14) + 2(16) + 4(18) + (2)] ≈ 2280559 The value of the integral produced by a calculator is 2280526 (to six decimal places). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.1 ARC LENGTH ¤ 5 29. (a) Let () = = √3 4 − with 0 ≤ ≤ 4. (b) The polygon with one side is just the line segment joining the points (0 (0)) = (00) and (4 (4)) = (40), and its length 1 = 4. The polygon with two sides joins the points (00), (2 (2)) = 22 √3 2 and (40). Its length 2 = (2 − 0)2 + 2 √3 2 − 02 + (4 − 2)2 + 0 − 2 √3 22 = 2√4 + 283 ≈ 643 Similarly, the inscribed polygon with four sides joins the points (00), 1 √3 3, 22 √3 2, (33), and (4 0), so its length 4 = 1 + √3 32 + 1 + 2 √3 2 − √3 32 + 1 + 3 − 2 √3 22 + √1 + 9 ≈ 750 (c) Using the arc length formula with = 1 3(4 − )−23(−1) + √3 4 − = 3(4 12−−4)23 , the length of the curve is = 04 1 + 2 = 04 1 + 3(4 12−−4)23 2 . (d) According to a calculator, the length of the curve is ≈ 77988. The actual value is larger than any of the approximations in part (b). This is always true, since any approximating straight line between two points on the curve is shorter than the length of the curve between the two points. 30. (a) Let () = = + sin with 0 ≤ ≤ 2. (b) The polygon with one side is just the line segment joining the points (0 (0)) = (0 0) and (2 (2)) = (22), and its length is (2 − 0)2 + (2 − 0)2 = 2√2 ≈ 89. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.6 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION The polygon with two sides joins the points (00), ( ()) = ( ), and (22). Its length is ( − 0)2 + ( − 0)2 + (2 − )2 + (2 − )2 = √2 + √2 = 2√2 ≈ 89 Note from the diagram that the two approximations are the same because the sides of the two-sided polygon are in fact on the same line, since () = = 1 2(2). The four-sided polygon joins the points (0 0), 2 2 + 1, ( ), 32 32 − 1, and (2 2), so its length is 2 2 + 2 + 12 + 2 2 + 2 − 12 + 2 2 + 2 − 12 + 2 2 + 2 + 12 ≈ 94 (c) Using the arc length formula with = 1 + cos, the length of the curve is = 02 1 + (1 + cos)2 = 02 √2 + 2 cos + cos2 (d) The calculator approximates the integral as 95076. The actual length is larger than the approximations in part (b). 31. = ⇒ = ⇒ 1 + ()2 ⇒ 1 + 2 ⇒ = 02 1 + 2 = 12 1 + 2 1 == 23 = √1 + 2 − ln 1 + √1 + 2 12 = √1 + 4 − ln 1 + √1 + 2 4 − √2 − ln 1 +1√2 = √1 + 4 − ln(1 + √1 + 4 ) + 2 − √2 + ln(1 + √2) ≈ 6788651 An equivalent answer from a CAS is −√2 + arctanh(√22) + √4 + 1 − arctanh(1√4 + 1 ). 32. = 43 ⇒ = 4 313 ⇒ 1 + ()2 = 1 + 16 9 23 ⇒ = 01 1 + 16 9 23 = 043 √1 + 2 81 642 == 4 39 41233, == 9 44 9 · −16 9232 , = 81 64 2 22 = 81 64 1 8(1 + 22)√1 + 2 − 1 8 ln + √1 + 2 4 03 = 81 64 1 61 + 32 9 25 9 − 1 8 ln 4 3 + 25 9 = 81 64 1 6 · 41 9 · 5 3 − 1 8 ln 3 = 205 128 − 512 81 ln 3 ≈ 14277586 33. 23 = 1 − 23 ⇒ = (1 − 23)32 ⇒ = 3 2 (1 − 23)12− 2 3−13 = −−13(1 − 23)12 ⇒ 2 = −23(1 − 23) = −23 − 1. Thus = 401 1 + (−23 − 1) = 401 −13 = 4 lim →0+ 3 2231 = 6. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.1 ARC LENGTH ¤ 7 34. (a) (b) = 23 ⇒ 1 + 2 = 1 + 2 3−132 = 1 + 4 9 −23. So = 01 1 + 4 9 −23 [an improper integral]. = 32 ⇒ 1 + 2 = 1 + 3 2122 = 1 + 9 4 . So = 01 1 + 9 4 . The second integral equals 4 9 · 2 31 + 9 4 321 0 = 27 8 13 √8 13 − 1 = 13 √27 13 − 8. The first integral can be evaluated as follows: 01 1 + 4 9 −23 = lim →0+ 1 √932133+ 4 = lim →0+ 9923 √18+ 4 = 9 = 62−133 = 09 √18+ 4 = 18 1 · 23( + 4)329 0 = 27 1 (1332 − 432) = 13√13 27 − 8 (c) = length of the arc of this curve from (−1 1) to (84) = 01 1 + 9 4 + 04 1 + 9 4 = 13√27 13 − 8 + 27 8 1 + 9 4324 0 [from part (b)] = 13√13 − 8 27 + 8 2710√10 − 1 = 13√13 + 80 27√10 − 16 35. = 232 ⇒ 0 = 312 ⇒ 1 + (0)2 = 1 + 9. The arc length function with starting point 0(1 2) is () = 1 √1 + 9 = 27 2 (1 + 9)32 1 = 27 2 (1 + 9)32 − 10√10. 36. (a) = () = ln(sin) ⇒ 0 = 1 sin · cos = cot ⇒ 1 + (0)2 = 1 + cot2 = csc2 ⇒ 1 + (0)2 = √csc2 = |csc|. Therefore, () = 2 1 + [ 0()]2 = 2 csc = ln|csc − cos| 2 = ln|csc − cot| − ln|1 − 0| = ln(csc − cot) (b) Note that is increasing on (0 ) and that = 0 and = are vertical asymptotes for both and . 37. = sin−1 + √1 − 2 ⇒ 0 = √1 1− 2 − √1− 2 = √11−−2 ⇒ 1 + (0)2 = 1 + (1 − )2 1 − 2 = 1 − 2 + 1 − 2 + 2 1 − 2 = 2 − 2 1 − 2 = 2(1 − ) (1 + )(1 − ) = 2 1 + ⇒ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.8 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 1 + (0)2 = 1 +2 . Thus, the arc length function with starting point (01) is given by () = 0 1 + [ 0()]2 = 0 1 +2 = √22√1 + 0 = 2√2√1 + − 1. 38. (a) () = 1 + [ 0()]2 and () = 0 √3 + 5 ⇒ 1 + [ 0()]2 = 3 + 5 ⇒ [ 0()]2 = 3 + 4 ⇒ 0() = √3 + 4 [since is increasing]. So () = (3 + 4)12 = 2 3 · 1 3(3 + 4)32 + and since has -intercept 2, (0) = 2 9 · 8 + and (0) = 2 ⇒ = 2 − 16 9 = 2 9 . Thus, () = 2 9(3 + 4)32 + 2 9 . (b) () = 0 √3 + 5 = 2 9(3 + 5)32 0 = 2 9(3 + 5)32 − 2 9(5)32. () = 3 ⇔ 2 9(3 + 5)32 = 3 + 2 9(5√5) ⇔ (3 + 5)32 = 27 2 + 5√5 ⇔ 3 + 5 = 27 2 + 5√523 ⇒ 1 = 1 3 27 2 + 5√523 − 5. Thus, the point on the graph of that is 3 units along the curve from the -intercept is (1 (1)) ≈ (11594765). 39. () = 1 4 + − ⇒ 0() = 1 4 − − ⇒ 1 + [ 0()]2 = 1 + 1 4 − −2 = 1 + 16 1 2 − 1 2 + −2 = 16 1 2 + 1 2 + −2 = 1 4 + −2 = [()]2. The arc length of the curve = () on the interval [ ] is = 1 + [ 0()]2 = [()]2 = (), which is the area under the curve = () on the interval [ ]. 40. = 150 − 40 1 ( − 50)2 ⇒ 0 = − 20 1 ( − 50) ⇒ 1 + (0)2 = 1 + 2012 ( − 50)2, so the distance traveled by the kite is = 080 1 + 20 12 ( − 50)2 = −3522 1 + 2 (20) == 20 20 11 ( − 50), 21 = 20 1 2 √1 + 2 + 1 2 ln + √1 + 2 3 −522 = 10 3 2 13 4 + ln 3 2 + 13 4 + 5 2 29 4 − ln− 5 2 + 29 4 = 15 2 √13 + 25 2 √29 + 10 ln −3 + 5 +√√13 29 ≈ 1228 ft 41. The prey hits the ground when = 0 ⇔ 180 − 45 1 2 = 0 ⇔ 2 = 45 · 180 ⇒ = √8100 = 90, since must be positive. 0 = − 45 2 ⇒ 1 + (0)2 = 1 + 4542 2, so the distance traveled by the prey is = 090 1 + 45 42 2 = 04 1 + 2 45 2 == 45 45 22 , 21 = 45 2 1 2 √1 + 2 + 1 2 ln + √1 + 2 4 0= 45 2 2√17 + 1 2 ln4 + √17 = 45√17 + 45 4 ln4 + √17 ≈ 2091 m 42. Let = − cosh, where = 21149, = 2096, and = 003291765. Then 0 = −sinh ⇒ 1 + (0)2 = 1 + 22 sinh2(). So = −9191 22 1 + 22 sinh2() ≈ 451137 ≈ 451, to the nearest meter. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.1 ARC LENGTH ¤ 9 43. The sine wave has amplitude 1 and period 14, since it goes through two periods in a distance of 28 in., so its equation is = 1 sin 214 = sin 7 . The width of the flat metal sheet needed to make the panel is the arc length of the sine curve from = 0 to = 28. We set up the integral to evaluate using the arc length formula with = 7 cos 7 : = 028 1 + 7 cos 7 2 = 2014 1 + 7 cos 7 2 . This integral would be very difficult to evaluate exactly, so we use a CAS, and find that ≈ 2936 inches. 44. (a) = + cosh ⇒ 0 = sinh ⇒ 1 + (0)2 = 1 + sinh2 = cosh2 . So = − cosh2 = 20 cosh = 2sinh 0 = 2sinh . (b) At = 0, = + , so + = 20. The poles are 50 ft apart, so = 25, and = 51 ⇒ 51 = 2sinh() [from part (a)]. From the figure, we see that = 51 intersects = 2sinh(25) at ≈ 723843 for 0. So ≈ 723843 and the wire should be attached at a distance of = + cosh(25) = 20 − + cosh(25) ≈ 2436 ft above the ground. 45. = 1 √3 − 1 ⇒ = √3 − 1 [by FTC1] ⇒ 1 + ()2 = 1 + √3 − 12 = 3 ⇒ = 14 √3 = 14 32 = 2 5 524 1 = 2 5(32 − 1) = 62 5 = 124 46. By symmetry, the length of the curve in each quadrant is the same, so we’ll find the length in the first quadrant and multiply by 4. 2 + 2 = 1 ⇒ 2 = 1 − 2 ⇒ = (1 − 2)1(2) (in the first quadrant), so we use the arc length formula with = 1 2(1 − 2)1(2)−1(−22−1) = −2−1(1 − 2)1(2)−1 The total length is therefore 2 = 401 1 + [−2−1(1 − 2)1(2)−1]2 = 401 1 + 2(2−1)(1 − 2)1−2 Now from the graph, we see that as increases, the “corners” of these fat circles get closer to the points (±1 ±1) and (±1 ∓1), and the “edges” of the fat circles approach the lines joining these four points. It seems plausible that as → ∞, the total length of the fat circle with = 2 will approach the length of the perimeter of the square with sides of length 2. This is supported by taking the limit as → ∞ of the equation of the fat circle in the first quadrant: lim →∞ (1 − 2)1(2) = 1 for 0 ≤ 1. So we guess that lim →∞ 2 = 4 · 2 = 8. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.10 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION DISCOVERY PROJECT Arc Length Contest For advice on how to run the contest and a list of student entries, see the article “Arc Length Contest” by Larry Riddle in The College Mathematics Journal, Volume 29, No. 4, September 1998, pages 314–320. 8.2 Area of a Surface of Revolution 1. (a) (i) = tan ⇒ = sec2 ⇒ = 1 + ()2 = √1 + sec4 . By (7), an integral for the area of the surface obtained by rotating the curve about the -axis is = 2 = 03 2 tan√1 + sec4 . (ii) By (8), an integral for the area of the surface obtained by rotating the curve about the -axis is = 2 = 03 2√1 + sec4 . (b) (i) 105017 (ii) 79353 2. (a) (i) = −2 ⇒ = −2−3 ⇒ = 1 + ()2 = √1 + 4−6 . By (7), = 2 = 12 2−2√1 + 4−6 . (ii) By (8), = 2 = 12 2√1 + 4−6 . (b) (i) 44566 (ii) 117299 3. (a) (i) = −2 ⇒ = −2 · (−2) ⇒ = 1 + ()2 = 1 + 42−22 . By (7), = 2 = −11 2−21 + 42−22 . (ii) By (8), = 2 = 01 21 + 42−22 [symmetric about the y-axis] (b) (i) 110753 (ii) 39603 4. (a) (i) = ln(2 + 1) ⇒ = 2 2 + 1 ⇒ = 1 + ()2 = 1 + 4(2 + 1)2 . By (7), = 2 = 01 2 1 + 4(2 + 1)2 . (ii) By (8), = 2 = 01 2 ln(2 + 1)1 + 4(2 + 1)2 . (b) (i) 42583 (ii) 56053 5. (a) (i) = + 3 ⇒ = 1 + 32 ⇒ = 1 + ()2 = 1 + (1 + 32)2 . By (7), = 2 = 01 2 1 + (1 + 32)2 . (ii) By (8) , = 2 = 01 2( + 3)1 + (1 + 32)2 . (b) (i) 85302 (ii) 135134 6. (a) (i) = tan−1 ⇒ = 1(1 + 2) ⇒ = 1 + ()2 = 1 + 1(1 + 2)2 . By (7), = 2 = 02 2 tan−1 1 + 1(1 + 2)2 . (ii) By (8), = 2 = 02 2 1 + 1(1 + 2)2 . (b) (i) 97956 (ii) 137209 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.2 AREA OF A SURFACE OF REVOLUTION ¤ 11 7. = 3 ⇒ 0 = 32. So = 02 2 1 + (0)2 = 2 02 3 √1 + 94 = 236 1145 √ [ = 1 + 94, = 363 ] = 18 2 3 32145 1 = 27 145√145 − 1 8. = √5 − ⇒ 0 = 1 2(5 − )−12(−1) = −1(2√5 − ). So = 35 21 + (0)2 = 35 2√5 − 1 + 4(51− ) = 2 35 5 − + 1 4 = 2 35 21 4 − = 2 9144 √(−) == −21 4 − , = 2 1944 12 = 2 2 3329 1 4 4 = 43 27 8 − 1 8 = 133 9. 2 = + 1 ⇒ = √ + 1 (for 0 ≤ ≤ 3 and 1 ≤ ≤ 2) ⇒ 0 = 1(2√ + 1 ). So = 03 21 + (0)2 = 2 03 √ + 11 + 4(1+ 1) = 2 03 + 1 + 1 4 = 2 03 + 5 4 = 2 517 44 √ == + 5 4 = 2 2 3 3217 544 = 2 · 23 17832 − 5382 = 6 (17√17 − 5√5). 10. = √1 + ⇒ 0 = 1 2(1 + )−12() = 2√1 + ⇒ 1 + (0)2 = 1 + 4(1 + 2) = 4 + 4 4(1 + +)2 = 4(1 + ( + 2) 2) = 2√1 + + 2 . So = 01 2 1 + (0)2 = 2 01 √1 + 2√1 + + 2 = 01( + 2) = + 21 0 = [( + 2) − (1 + 0)] = ( + 1) 11. = cos 1 2 ⇒ 0 = − 1 2 sin 1 2 . So = 0 21 + (0)2 = 2 0 cos 1 2 1 + 1 4 sin2 1 2 = 2 01 1 + 1 42 (2) = sin = 1 2 cos 1 2 1 2, = 2 01 4 + 2 = 2 21 24 + 2 + 2 ln + 4 + 2 1 0 = 2 1 2√5 + 2 ln(1 + √5) − (0 + 2 ln 2) = √5 + 4 ln1 +2√5 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.12 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 12. = 3 6 + 1 2 ⇒ = 2 2 − 1 22 ⇒ 1 + 2 = 44 + 1 2 + 414 = 22 + 212 2 = 22 + 212 ⇒ = 112 263 + 2122 + 212 = 2 112 125 + 12 + 4 + 413 = 2 112 125 + 3 + −4 3 = 2726 + 62 − −8 2 1 12 = 2 72 1 + 1 6 − 1 8 − 641· 72 + 24 1 − 1 2 = 2 263 512 = 263 256 13. = 1 3(2 + 2)32 ⇒ = 1 2(2 + 2)12(2) = 2 + 2 ⇒ 1 + ()2 = 1 + 2(2 + 2) = (2 + 1)2. So = 2 12 (2 + 1) = 2 1 4 4 + 1 2 22 1 = 24 + 2 − 1 4 − 1 2 = 212 . 14. = 1 + 22 ⇒ 1 + ()2 = 1 + (4)2 = 1 + 162. So = 2 12 1 + 162 = 16 12(162 + 1)1232 = 16 2 3(162 + 1)322 1 = 24 65√65 − 17√17. 15. = 1 3 32 ⇒ 0 = 1 2 12 ⇒ 1 + (0)2 = 1 + 1 4 . So = 012 21 + (0)2 = 2 012 1 + 1 4 = 2 012 1 2√4 + = 416( − 4)√ == + 4 = 416(32 − 412) = 2 5 52 − 8 3 3216 4 = 2 5 · 1024 − 8 3 · 64 − 2 5 · 32 − 8 3 · 8 = 2 5 · 992 − 8 3 · 56 = 595215 − 2240 = 3712 15 16. 23 + 23 = 1, 0 ≤ ≤ 1. The curve is symmetric about the -axis from = −1 to = 1, so we’ll use the portion of the curve from = 0 to = 1. 23 = 1 − 23 ⇒ = (1 − 23)32 ⇒ 0 = 3 2(1 − 23)12 − 2 3 −13 = −√1−13 23 ⇒ 1 + (0)2 = 1 + 1 −2323 = 23 + 1 23− 23 = −23. So = 01 21 + (0)2 = 2 01 (−13) = 2 01 23 = 2 3 5 531 0 = 2 3 5 = 65 . 17. = 2 − 2 ⇒ = 1 2(2 − 2)−12(−2) = −2 − 2 ⇒ 1 + 2 = 1 + 2 −2 2 = 2 2 − − 2 2 + 2 −2 2 = 2 −2 2 ⇒ = 02 2 2 − 2 2− 2 = 2 02 = 2 0 2 = 22 − 0 = 2. Note that this is 1 4 the surface area of a sphere of radius , and the length of the interval = 0 to = 2 is 1 4 the length of the interval = − to = . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.2 AREA OF A SURFACE OF REVOLUTION ¤ 13 18. = 1 4 2 − 1 2 ln ⇒ = 2 − 21 ⇒ 1 + 2 = 1 + 42 − 12 + 412 = 42 + 12 + 412 = 2 + 212. So = 12 2 2 + 212 = 2 12 2 + 21 = 12(2 + 1) = 1 33 + 2 1 = 8 3 + 2 − 1 3 + 1 = 10 3 19. = 1 5 5 ⇒ = 4 ⇒ 1 + ()2 = 1 + 8 ⇒ = 05 2 1 55 √1 + 8 . Let () = 2 55√1 + 8. Since = 10, ∆ = 5 10 − 0 = 1 2 . Then ≈ 10 = 132[(0) + 4(05) + 2(1) + 4(15) + 2(2) + 4(25) + 2(3) + 4(35) + 2(4) + 4(45) + (5)] ≈ 1,230,507 The value of the integral produced by a calculator is approximately 1,227,192. 20. = + 2 ⇒ = 1 + 2 ⇒ 1 + ()2 = 1 + (1 + 2)2 ⇒ = 01 2( + 2)1 + (1 + 2)2 . Let () = 2( + 2)1 + (1 + 2)2. Since = 10, ∆ = 110 − 0 = 10 1 . Then ≈ 10 = 1310[(0) + 4(01) + 2(02) + 4(03) + 2(04) + 4(05) + 2(06) + 4(07) + 2(08) + 4(09) + (1)] ≈ 13649368 The value of the integral produced by a calculator is 13649370 (to six decimal places). 21. = ⇒ = + ⇒ 1 + ()2 = 1 + ( + )2 ⇒ = 01 21 + ( + )2 . Let () = 21 + ( + )2. Since = 10, ∆ = 110 − 0 = 10 1 . Then ≈ 10 = 1310[(0) + 4(01) + 2(02) + 4(03) + 2(04) + 4(05) + 2(06) + 4(07) + 2(08) + 4(09) + (1)] ≈ 24145807 The value of the integral produced by a calculator is 24144251 (to six decimal places). 22. = ln ⇒ = · 1 + ln = 1 + ln ⇒ 1 + ()2 = 1 + (1 + ln)2 ⇒ = 12 2ln 1 + (1 + ln)2 . Let () = 2ln 1 + (1 + ln)2. Since = 10, ∆ = 210 − 1 = 10 1 . Then ≈ 10 = 1310[(1) + 4(11) + 2(12) + 4(13) + 2(14) + 4(15) + 2(16) + 4(17) + 2(18) + 4(19) + (2)] ≈ 7248933 The value of the integral produced by a calculator is 7248934 (to six decimal places). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.14 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 23. = 1 ⇒ = 1 + ()2 = 1 + (−12)2 = 1 + 14 ⇒ = 12 2 · 1 1 + 14 = 2 12 √43+ 1 = 2 14 √22+ 1 1 2 [ = 2, = 2 ] = 14 √1 + 2 2 =24 −√1 + 2 + ln + 1 + 2 4 1 = − √417 + ln4 + √17 + √12 − ln1 + √2 = 4 4ln√17 + 4 − 4ln√2 + 1 − √17 + 4√2 24. = √2 + 1 ⇒ = √2 + 1 ⇒ = 1 + 2 = 1 + 2+ 1 2 ⇒ = 03 2 2 + 1 1 + 2+ 1 2 = 2 03 22 + 1 = 2√2 03 2 + √122 21 = 2√2 1 2 2 + 1 2 + 1 4 ln + 2 + 1 2 3 0 = 2√2 3 29 + 1 2 + 1 4 ln3 + 9 + 1 2 − 1 4 ln √12 = 2√2 3 2 19 2 + 1 4 ln3 + 19 2 + 1 4 ln√2 = 2√2 3 2 √√19 2 + 1 4 ln3√2 + √19 = 3√19 + √2 ln3√2 + √19 25. = 3 and 0 ≤ ≤ 1 ⇒ 0 = 32 and 0 ≤ ≤ 1. = 01 2 1 + (32)2 = 2 03 √1 + 2 16 = 3 = 6 2, = 3 03 √1 + 2 21 = [or use CAS] 3 1 2 √1 + 2 + 1 2 ln + √1 + 2 3 0 = 3 3 2 √10 + 1 2 ln3 + √10 = 6 3√10 + ln3 + √10 26. = ln( + 1), 0 ≤ ≤ 1. = 1 + 2 = 1 + + 1 1 2 , so = 01 2 1 + ( + 1) 1 2 = 12 2( − 1)1 + 12 [ = + 1, = ] = 2 12 √1 + 2 − 2 12 √1 + 2 = 2 12 1 + 2 − 2 12 √1 + 2 21, 23 = [or use CAS] 2 1 2 √1 + 2 + 1 2 ln + √1 + 2 2 1 − 2√1 + 2 − ln1 + √1 + 2 2 1 = 2√5 + 1 2 ln2 + √5 − 1 2√2 − 1 2 ln1 + √2 − 2√5 − ln 1 +2√5 − √2 + ln1 + √2 = 2 1 2 ln2 + √5 + ln 1 +2√5 + √22 − 3 2 ln1 + √2 27. = 2 1∞ 1 + 2 = 2 1∞ 1 1 + 14 = 2 1∞ √43+ 1 . Rather than trying to evaluate this integral, note that √4 + 1 √4 = 2 for 0. Thus, if the area is finite, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.2 AREA OF A SURFACE OF REVOLUTION ¤ 15 = 2 1∞ √43+ 1 2 1∞ 2 3 = 2 1∞ 1 . But we know that this integral diverges, so the area is infinite. 28. = 0∞ 2 1 + ()2 = 2 0∞ −1 + (−−)2 [ = −, 0 = −−]. Evaluate = −1 + (−−)2 by using the substitution = −−, = − : = √1 + 2 =21 1 2 √1 + 2 + 1 2 ln + √1 + 2 + = 1 2(−−)√1 + −2 + 1 2 ln−− + √1 + −2 + . Returning to the surface area integral, we have = 2 lim →∞ 0 −1 + (−−)2 = 2 lim →∞ 1 2(−−)√1 + −2 + 1 2 ln−− + √1 + −2 0 = 2 lim →∞ 1 2(−−)√1 + −2 + 1 2 ln−− + √1 + −2 − 1 2(−1)√1 + 1 + 1 2 ln−1 + √1 + 1 = 2 1 2(0)√1 + 1 2 ln0 + √1 − − 1 2√2 + 1 2 ln−1 + √2 = 2[0] + 1 2√2 − ln√2 − 1 = √2 − ln√2 − 1 29. Since 0, the curve 32 = ( − )2 only has points with ≥ 0. [32 ≥ 0 ⇒ ( − )2 ≥ 0 ⇒ ≥ 0.] The curve is symmetric about the x-axis (since the equation is unchanged when is replaced by −). = 0 when = 0 or , so the curve’s loop extends from = 0 to = . (32) = [( − )2] ⇒ 6 = · 2( − )(−1) + ( − )2 ⇒ = ( − )[−62 + − ] ⇒ 2 = ( − 36 )2(2−2 3)2 = ( − )36 2(2− 3)2 · (3−)2 the last fraction is 12 = (12 − 3)2 ⇒ 1 + 2 = 1 + 2 − 612 + 92 = 12 12 + 2 − 612 + 92 = 2 + 612 + 92 = (12 + 3 )2 for 6= 0. (a) = =0 2 = 2 0 √√(3− ) · √ + 3 12 = 2 0 ( − )( 6 + 3) = 3 0(2 + 2 − 32) = 32 + 2 − 3 0 = 3(3 + 3 − 3) = 3 · 3 = 32 . Note that we have rotated the top half of the loop about the x-axis. This generates the full surface. (b) We must rotate the full loop about the -axis, so we get double the area obtained by rotating the top half of the loop: = 2 · 2 =0 = 4 0 √ + 3 12 = 2√43 0 12( + 3) = √23 0(12 + 332) = 2 √3 2 332 + 6552 0 = 23√√3 2 352 + 6552 = 23√3 2 3 + 652 = 23√3 28 152 = 56 √32 45 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.16 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 30. In general, if the parabola = 2, − ≤ ≤ , is rotated about the -axis, the surface area it generates is 2 0 1 + (2)2 = 2 02 21 + 2 21 = 2 = 2 , = 42 02 1 + 212 2 = 42 2 31 + 2322 0 = 62 1 + 42232 − 1 Here 2 = 10 ft and 2 = 2 ft, so = 5 and = 25 2 . Thus, the surface area is = 6 625 4 1 + 4 · 625 4 · 2532 − 1 = 625 24 1 + 16 2532 − 1 = 625 24 41125 √41 − 1 = 524 41√41 − 125 ≈ 9001 ft2. 31. (a) 2 2 + 2 2 = 1 ⇒ ( 2 ) = −2 ⇒ = −22 ⇒ 1 + 2 = 1 + 4422 = 424+242 = 424+2(1 42−1−222 ) 2 = 42+424−22−22222 = 4 + 22 − 22 4 − 22 = 4 − 2 − 22 2(2 − 2) The ellipsoid’s surface area is twice the area generated by rotating the first-quadrant portion of the ellipse about the -axis. Thus, = 20 2 1 + 2 = 4 0 2 − 2 4−√(22−−22)2 = 4 2 0 4 − (2 − 2)2 = 4 2 0√2−24 − 2 √2− 2 = √2 − 2 =30 2√4 2 − 224 − 2 + 24 sin−12 0√2−2 = 4 2√2 − 2 √22 − 2 4 − 2(2 − 2) + 24 sin−1 √2− 2 = 2 2 + 2sin−1 √2 − 2 √2 − 2 (b) 2 2 + 2 2 = 1 ⇒ ( 2 ) = −2 ⇒ = −22 ⇒ 1 + 2 = 1 + 4422 = 424+242 = 42(1 4−2(12−22) + 2)42 = 24−242−2222+242 = 4 − 22 + 22 4 − 22 = 4 − (2 − 2)2 2(2 − 2) The oblate spheroid’s surface area is twice the area generated by rotating the first-quadrant portion of the ellipse about the -axis. Thus, = 20 2 1 + 2 = 4 0 2 − 2 4−(22−−22)2 = 4 2 0 4 − (2 − 2)2 = 4 2 0 4 + (2 − 2) 2 since = 4 2 0√2−2 4 + 2 √2− 2 = √2 − 2 21 = 4 2√2 − 2 2 √4 + 2 + 24 ln + √4 + 2 0√2−2 [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.2 AREA OF A SURFACE OF REVOLUTION ¤ 17 = 4 2√2 − 2 √22− 2 () + 24 ln √2 − 2 + − 0 + 24 ln(2) = 4 2√2 − 2 2√22 − 2 + 24 ln √2 −22 + = 22 + √2 2 −22 ln √2 −2 + 32. The upper half of the torus is generated by rotating the curve ( − )2 + 2 = 2, 0, about the -axis. = −( − ) ⇒ 1 + 2 = 1 + ( −2)2 = 2 + (2− )2 = 2 − (2− )2 . Thus, = 2−+ 2 1 + 2 = 4 −+ 2 − ( − )2 = 4 − √2+−2 = − = 4 − √ 2 − 2 + 4 − √2− 2 = 4 · 0 + 8 0 √2− 2 since the first integrand is odd and the second is even = 8sin−1() 0 = 8 2 = 42 33. The analogue of (∗ ) in the derivation of (4) is now − (∗ ), so = lim →∞ =1 2[ − (∗ )]1 + [ 0(∗ )]2 ∆ = 2[ − ()]1 + [ 0()]2 . 34. = 12 ⇒ 0 = 1 2−12 ⇒ 1 + (0)2 = 1 + 14, so by Exercise 31, = 04 24 − √ 1 + 1(4). Using a CAS, we get = 2 ln√17 + 4 + 6 31√17 + 1 ≈ 806095. 35. For the upper semicircle, () = √2 − 2, 0() = −√2 − 2. The surface area generated is 1 = − 2 − 2 − 2 1 + 2 −22 = 4 0 − 2 − 2 √2− 2 = 4 0 √2−2 2 − For the lower semicircle, () = −√2 − 2 and 0() = √2− 2 , so 2 = 4 0 √2−2 2 + . Thus, the total area is = 1 + 2 = 8 0 √2−2 2 = 82 sin−1 0 = 822 = 422. 36. (a) Rotate = √2 − 2 with ≤ ≤ + about the -axis to generate a zone of a sphere. = √2 − 2 ⇒ 0 = 1 2(2 − 2)−12(−2) ⇒ = 1 + √−2 − 2 2 . The surface area is = + 2 = 2 + 2 − 21 + 2−2 2 = 2 + 2 − 2 + 2 = 2 + = 2( + − ) = 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.18 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION (b) Rotate = with 0 ≤ ≤ about the -axis to generate a zone of a cylinder. = ⇒ 0 = 0 ⇒ = √1 + 02 = . The surface area is = 0 2 = 2 0 = 2 0 = 2. 37. = 2 + −2 ⇒ 0 = 1 2 2 − 1 2 −2 ⇒ 1 + (0)2 = 1 + 1 2 2 − 1 2−22 = 1 + 1 4 − 1 2 + 1 4 − = 1 4 + 1 2 + 1 4 − = 1 2 2 + 1 2−22. If we rotate the curve about the -axis on the interval ≤ ≤ , the resulting surface area is = 21 + (0)2 = 2 (2 + −2) 1 22 + 1 2 −2 = (2 + −2)2 , which is the same as the volume obtained by rotating the curve about the -axis on the interval ≤ ≤ , namely, = 2 . 38. Since () = () + , we have 0() = 0(). Thus, = 2()1 + [0()]2 = 2[() + ]1 + [ 0()]2 = 2()1 + [ 0()]2 + 2 1 + [ 0()]2 = + 2 39. In the derivation of (4), we computed a typical contribution to the surface area to be 2 −1 + 2 |−1|, the area of a frustum of a cone. When () is not necessarily positive, the approximations = () ≈ (∗ ) and −1 = (−1) ≈ (∗ ) must be replaced by = |()| ≈ |(∗ )| and −1 = |(−1)| ≈ |(∗ )|. Thus, 2 −1 + 2 |−1| ≈ 2 |(∗ )| 1 + [ 0(∗ )]2 ∆. Continuing with the rest of the derivation as before, we obtain = 2 |()| 1 + [ 0()]2 . DISCOVERY PROJECT Rotating on a Slant 1. In the figure, the segment lying above the interval [ − ∆ ] along the tangent to has length °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.DISCOVERY PROJECT ROTATING ON A SLANT ¤ 19 ∆sec = ∆ √1 + tan2 = 1 + [ 0()]2 ∆. The segment from ( ()) drawn perpendicular to the line = + has length () = [() − − ]cos = () − − sec = () − − 1 + tan2 = () − − √1 + 2 Also, cos( − ) = ∆ ∆ sec ⇒ ∆ = ∆ sec cos( − ) = ∆ cos cos + sin sin cos = ∆(cos + sin tan) = ∆ √1 +1 2 + √1 + 2 0() = 1 + √1 + 0(2) ∆ Thus, Area(R) = lim →∞ =1 ()∆ = lim →∞ =1 () − − √1 + 2 · 1 + 0() √1 + 2 ∆ = 1 1 + 2 [() − − ][1 + 0()] 2. From Problem 1 with = 1, () = + sin, + = − 2, = 0, and = 2, Area = 1 1 + 12 02 [ + sin − ( − 2)] [1 + 1(1 + cos)] = 1 2 02(sin + 2)(2 + cos) = 1 2 02(2 sin + sin cos + 4 + 2 cos ) = 1 2−2cos + 1 2 sin2 + 4 + 2 sin2 0 = 1 2 [(−2 + 0 + 8 + 0) − (−2 + 0 + 0 + 0)] = 1 2(8) = 4 3. = lim →∞ =1 [()]2 ∆ = lim →∞ =1 (√)1 + − 2 − 2 1 + √1 + 0(2) ∆ = (1 + 2)32 [() − − ]2[1 + 0()] 4. = (1 + 12)32 02( + sin − + 2)2(1 + 1 + cos ) = 2√2 02(sin + 2)2(cos + 2) = 2√ 2 02sin2 + 4 sin + 4(cos + 2) = 2√2 02sin2 cos + 4 sin cos + 4 cos + 2 sin2 + 8 sin + 8 = 2√2 1 3 sin3 + 2 sin2 + 4 sin + − 1 2 sin 2 − 8cos + 82 0 [since 2 sin2 = 1 − cos 2] = 2√2[(2 − 8 + 16) − (−8)] = 9√2 2 2 5. = 2()1 + [ 0()]2 = √1 + 22 [() − − ]1 + [ 0()]2 6. From Problem 5 with () = √, = 0, = 4, = 1 2 , and = 0, = 1 +2 1 22 04 √ − 1 2 1 + 2√1 2 CAS = √5ln√17 + 4 32 + 3724 √17 − 13 ≈ 8554 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.20 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 8.3 Applications to Physics and Engineering 1. The weight density of water is = 625 lbft3. (a) = ≈ (625 lbft3)(3 ft) = 1875 lbft2 (b) = ≈ (1875 lbft2)(5 ft)(2 ft) = 1875 lb. ( is the area of the bottom of the tank.) (c) As in Example 1, the area of the th strip is 2(∆) and the pressure is = . Thus, = 03 · 2 ≈ (625)(2)03 = 125 1 2 23 0 = 125 9 2 = 5625 lb. 2. (a) = = (820 kgm3)(98 ms2)(15 m) = 12,054 Pa ≈ 12 kPa (b) = = (12,054 Pa)(8 m)(4 m) ≈ 386 × 105 N ( is the area at the bottom of the tank.) (c) The area of the th strip is 4(∆) and the pressure is = . Thus, = 015 · 4 = (820)(98) · 4015 = 32,144 1 2 23 02 = 16,072 9 4 ≈ 362 × 104 N. In Exercises 3–9, is the number of subintervals of length ∆ and ∗ is a sample point in the th subinterval [−1 ]. 3. Set up a vertical x-axis as shown, with = 0 at the water’s surface and increasing in the downward direction. Then the area of the th rectangular strip is 2∆ and the pressure on the strip is ∗ (where ≈ 625 lbft3). Thus, the hydrostatic force on the strip is ∗ · 2∆ and the total hydrostatic force ≈ =1 ∗ · 2∆. The total force x x *i wi 2 ft 8 ft =2 3 0 11 = lim →∞ =1 ∗ · 2∆ = 311 · 2 = 2 311 = 2 1 2 211 3 = (121 − 9) = 112 ≈ 7000 lb 4. Set up a vertical axis as shown. Then the area of the th rectangular strip is 2(∗ − 2)∆. By similar triangles, ∗ − 2 = 10 5 , so = 2(∗ − 2) The pressure on the strip is ∗ , so the hydrostatic force on the strip is ∗ · 2(∗ − 2)∆ and the total hydrostatic force on the plate ≈ =1 ∗ · 2(∗ − 2)∆. The total force = lim →∞ =1 ∗ · 2(∗ − 2)∆ = 27 · 2( − 2) = 2 27(2 − 2) = 2 1 3 3 − 27 2 = 2 343 3 − 49 − 8 3 − 4 = 2 200 3 = 400 3 ≈ 400 3 (625) = 83333 lb. 5. Set up a coordinate system as shown. Then the area of the th rectangular strip is 282 − (∗)2 ∆. The pressure on the strip is = (12 − ∗), so the hydrostatic force on the strip is (12 − ∗)264 − (∗)2 ∆ and the total hydrostatic force on the plate ≈ =1 (12 − ∗)264 − (∗)2 ∆. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 21 The total force = lim →∞ =1 (12 − ∗)264 − (∗)2 ∆ = −88 (12 − )264 − 2 = 2 · 12−88 64 − 2 − 2 −88 64 − 2 . The second integral is 0 because the integrand is an odd function. The first integral is the area of a semicircular disk with radius 8. Thus, = 24 1 2 (8)2 = 768 ≈ 768(1000)(98) ≈ 236 × 107 N. 6. Set up a coordinate system as shown. Then the area of the th rectangular strip is 262 − (∗)2 ∆. The pressure on the strip is = (4 − ∗), so the hydrostatic force on the strip is (4 − ∗)236 − (∗)2 ∆ and the hydrostatic force on the plate ≈ =1 (4 − ∗)236 − (∗)2 ∆. The total force = lim →∞ =1 (4 − ∗)236 − (∗)2 ∆ = 04 (4 − )236 − 2 = 81 − 22. 1 = 04 36 − 2 = 0 36 − 36 sin2 (6 cos ) = 6 sin = sin = 6 cos −1 (23) = 0 36 cos2 = 0 36 · 1 2(1 + cos 2) = 18 + 1 2 sin 2 0 = 18 + 1 2 sin 2 = 18( + sin cos). 2 = 04 36 − 2 = 36 20 √(− 1 2 ) = 36 = −2− 2 = − 1 2 2 33220 36 = − 1 3(2032 − 216) = 72 − 40 3 √5. Thus, = 8 · 18( + sin cos) − 272 − 40 3 √5 = 144sin−1 2 3 + 2 3 √35 − 272 − 40 3 √5 = 144 sin−1 2 3 + 176 3 √5 − 144 ≈ 904 × 105 N [ = 1000, ≈ 98]. 7. Set up a vertical x-axis as shown. Then the area of the th rectangular strip is 2 − √23 ∗ ∆. By similar triangles, 2 = √3√−3∗ , so = 2 − √23 ∗ . The pressure on the strip is ∗ , so the hydrostatic force on the strip is ∗ 2 − √23 ∗ ∆ and the hydrostatic force on the plate ≈ =1 ∗ 2 − √23 ∗ ∆. The total force = lim →∞ =1 ∗ 2 − √23 ∗ ∆ = 0√3 2 − √23 = 0√3 2 − √23 2 = 2 − 3√23 3√ 0 3 = [(3 − 2) − 0] = ≈ 1000 · 98 = 98 × 103 N °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.22 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 8. Set up a vertical -axis as shown. Then the area of the th rectangular strip is 3∗ ∆. By similar triangles, ∗ = 62, so = 3∗ . The pressure on the strip is (∗ + 4), so the hydrostatic force on the strip is (∗ + 4)3∗ ∆ and the hydrostatic force on the plate ≈ =1 (∗ + 4)3∗ ∆. The total force = lim →∞ =1 (∗ + 4)3∗ ∆ = 02 ( + 4)3 = 3 02(2 + 4) = 3 1 33 + 222 0 = 3 8 3 + 8 = 32 = 313,600 N [ = 1000, ≈ 98] 9. Set up a vertical -axis as shown. Then the area of the th rectangular strip is ∆ = 4 + 2 · 2 3∗ ∆. The pressure on the strip is (∗ − 1), so the hydrostatic force on the strip is (∗ − 1)4 + 4 3∗ ∆ and the hydrostatic force on the plate ≈ =1 (∗ − 1)4 + 4 3∗ ∆. The total force = lim →∞ =1 (∗ − 1)4 + 4 3∗ ∆ = 13 ( − 1)4 + 4 3 = 13 4 32 + 8 3 − 4 = 4 93 + 4 32 − 43 1 = (12 + 12 − 12) − 4 9 + 4 3 − 4 = 128 9 ≈ 889 lb [ ≈ 62.5] 10. Set up coordinate axes as shown in the figure. For the top half, the length of the th strip is 2√2 − ∗ and its area is 2√2 − ∗ ∆. The pressure on this strip is approximately = √2 − ∗ and so the force on the strip is approximately 2√2 − ∗2 ∆. The total force 1 = lim →∞ =1 2√2 − ∗2∆ = 2 0√2 √2 − 2 = 2−13 √2 − 3 0 √2 = −230 − √23 = 23 2√32 = √263 For the bottom half, the length is 2√2 + ∗ and the total force is 2 = lim →∞ =1 2√2 + ∗√2 − ∗ ∆ = 2 −0√2 22 − 2 = 2 1 22 − 1 330 −√2 = 20 − −√243 + √12 23 = 2√263 = 2√263 [2 = 21] Thus, the total force = 1 + 2 = 3√23 6 = √23 2 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 23 11. Set up a vertical x-axis as shown. Then the area of the th rectangular strip is (2 − ∗ )∆. By similar triangles, 2−∗ = 22, so = (2 − ∗ ) The pressure on the strip is ∗ , so the hydrostatic force on the plate ≈ =1 ∗ (2 − ∗ )∆. The total force = lim →∞ =1 ∗ (2 − ∗ )∆ = 0 (2 − ) = 0 2 − 2 = 2 − 1 33 0 = 3 − 1 33 = 233 = 2 32 12. (a) The solution is similar to the solution for Example 2. The pressure on a strip is approximately = 646(3 − ∗) and the total force is = lim →∞ =1 646(3 − ∗)29 − (∗)2 ∆ = 1292−33(3 − )9 − 2 = 1292 · 3−33 9 − 2 − 1292−33 9 − 2 = 3876 · 1 2(3)2 − 0 the first integral is the area of a semicircular disk with radius 3 and the second integral is 0 because the integrand is an odd function = (17442) ≈ 5480 lb (b) If the tank is half full, the surface of the milk is = 0, so the pressure on a strip is approximately = 646(0 − ∗). The upper limit of integration changes from 3 to 0 and the total force is = 1292−03(0 − )9 − 2 = 1292 1 3(9 − 2)320 −3 = 1292(9 − 0) = 11628 lb Note that this is about 21% of the force for a full tank. 13. By similar triangles, 8 4√3 = ∗ ⇒ = 2∗ √3 . The area of the th rectangular strip is 2√3∗ ∆ and the pressure on it is 4√3 − ∗ . = 04√3 4√3 − √23 = 8 04√3 − 2√ 3 04√3 2 = 4 2 4 0√3 − 2 3√3 3 4 0√3 = 192 − 2 3√3 64 · 3√3 = 192 − 128 = 64 ≈ 64(840)(98) ≈ 527 × 105 N 14. = 02 (10 − )2√4 − 2 = 20 02 √4 − 2 − 02 √4 − 2 2 = 20 1 4(22) − 04 12 [ = 4 − 2, = −2 ] = 20 − 2 3324 0 = 20 − 16 3 = 20 − 16 3 = (1000)(98)20 − 16 3 ≈ 563 × 105 N °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.24 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 15. (a) The top of the cube has depth = 1 m − 20 cm = 80 cm = 08 m. = ≈ (1000)(98)(08)(02)2 = 3136 ≈ 314 N (b) The area of a strip is 02∆ and the pressure on it is ∗ . = 018 (02) = 02 1 221 08 = (02)(018) = 0036 = 0036(1000)(98) = 3528 ≈ 353 N 16. The height of the dam is = √702 − 252 cos 30◦ = 15√19 √23 . The width of the trapezoid is = 50 + 2. By similar triangles, 25 = − ⇒ = 25 ( − ). Thus, = 50 + 2 · 25 ( − ) = 50 + 50 · − 50 · = 50 + 50 − 50 = 100 − 50 . From the small triangle in the second figure, cos 30◦ = ∆ ⇒ = ∆sec 30◦ = 2∆√3. = 0 100 − 50 √23 = 200 √3 0 − 100 √3 0 2 = 200 √3 2 2 − 100 √3 3 3 = 2002 3√3 = 200(625) 3√3 · 12,825 4 ≈ 771 × 106 lb 17. (a) The area of a strip is 20∆ and the pressure on it is . = 03 20 = 20 1 223 0 = 20 · 9 2 = 90 = 90(625) = 5625 lb ≈ 563 × 103 lb (b) = 09 20 = 20 1 229 0 = 20 · 81 2 = 810 = 810(625) = 50,625 lb ≈ 506 × 104 lb. (c) For the first 3 ft, the length of the side is constant at 40 ft. For 3 ≤ 9, we can use similar triangles to find the length : 40 = 9 − 6 ⇒ = 40 · 9 − 6 . = 03 40 + 39 (40) 9 −6 = 40 1 223 0 + 20 3 39(9 − 2) = 180 + 20 3 9 22 − 1 339 3 = 180 + 20 3 729 2 − 243 − 81 2 − 9 = 180 + 600 = 780 = 780(625) = 48,750 lb ≈ 488 × 104 lb (d) For any right triangle with hypotenuse on the bottom, sin = ∆ hypotenuse ⇒ hypotenuse = ∆csc = ∆ √402 + 62 6 = √409 3 ∆. = 39 20 √409 3 = 1 3 20√409 1 229 3 = 1 3 · 10√409(81 − 9) ≈ 303,356 lb ≈ 303 × 105 lb °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 25 18. Partition the interval [ ] by points as usual and choose ∗ ∈ [−1 ] for each . The th horizontal strip of the immersed plate is approximated by a rectangle of height ∆ and width (∗ ), so its area is ≈ (∗ )∆. For small ∆, the pressure on the th strip is almost constant and ≈ ∗ by Equation 1. The hydrostatic force acting on the th strip is = ≈ ∗ (∗ )∆. Adding these forces and taking the limit as → ∞, we obtain the hydrostatic force on the immersed plate: = lim →∞ =1 = lim →∞ =1 ∗ (∗ )∆ = () 19. From Exercise 18, we have = () = 7904 64(). From the table, we see that ∆ = 04, so using Simpson’s Rule to estimate , we get ≈ 64 04 3 [70(70) + 4(74)(74) + 2(78)(78) + 4(82)(82) + 2(86)(86) + 4(90)(90) + 94(94)] = 256 3 [7(12) + 296(18) + 156(29) + 328(38) + 172(36) + 36(42) + 94(44)] = 256 3 (48604) ≈ 4148 lb 20. (a) From Equation 8, = 1 () ⇒ = () ⇒ = () ⇒ () = () = by Exercise 18. (b) For the figure in Exercise 10, let the coordinates of the centroid ( ) = √20. = () = √2 2 = √22 2 = √223 . 21. The moment of the system about the origin is = 2 =1 = 11 + 22 = 6 · 10 + 9 · 30 = 330. The mass of the system is = 2 =1 = 1 + 2 = 6 + 9 = 15. The center of mass of the system is = = 330 15 = 22. 22. The moment is 11 + 22 + 33 = 12(−3) + 15(2) + 20(8) = 154. The mass is 1 + 2 + 3 = 12 + 15 + 20 = 47. The center of mass is = = 154 47 . 23. The mass is = 3 =1 = 4 + 2 + 4 = 10. The moment about the -axis is = 3 =1 = 4(−3) + 2(1) + 4(5) = 10. The moment about the -axis is = 3 =1 = 4(2) + 2(−3) + 4(3) = 14. The center of mass is ( ) = = 14 10 10 10 = (141). 24. The mass is = 4 =1 = 5 + 4 + 3 + 6 = 18. The moment about the -axis is = 4 =1 = 5(2) + 4(5) + 3(2) + 6(−2) = 24. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.26 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION The moment about the -axis is = 4 =1 = 5(−4) + 4(0) + 3(3) + 6(1) = −5. The center of mass is ( ) = = −185 24 18 = −18 5 43. 25. The region in the figure is “right-heavy” and “bottom-heavy,” so we know that 05 and 1, and we might guess that = 07 and = 07. = 01 2 = 21 0 = 1 − 0 = 1. = 1 01 (2) = 1 1 2 331 0 = 2 3 = 1 01 1 2(2)2 = 1 1 01 22 = 2 3 31 0 = 2 3. Thus, the centroid is ( ) = 2 3 2 3. 26. The region in the figure is “right-heavy” and “bottom-heavy,” so we know that 2 and 1, and we might guess that = 23 and = 08. = 04 √ = 2 3 324 0 = 16 3 . = 1 04 (√) = 16 3 04 32 = 16 3 2 5 524 0 = 40 3 (32 − 0) = 12 5 . = 1 04 1 2(√)2 = 16 3 04 1 2 = 32 3 1 2 24 0 = 64 3 (16 − 0) = 3 4. Thus, the centroid is ( ) = (24 075). 27. The region in the figure is “right-heavy” and “bottom-heavy,” so we know 05 and 1, and we might guess that = 06 and = 09. = 01 = []1 0 = − 1. = 1 01 = −1 1[ − ]1 0 [by parts] = 1 − 1[0 − (−1)] = −1 1. = 1 01 1 2()2 = −1 1 · 1 421 0 = 4(1− 1)2 − 1 = + 1 4 . Thus, the centroid is ( ) = −1 1 + 1 4 ≈ (058 093). 28. Since the region in the figure is symmetric about the line = 2 , we know that = 2 . The region is “bottom-heavy,” so we know that 05, and we might guess that = 04. = 0 sin = −cos 0 = 1 − (−1) = 2. = 1 0 sin 82 = 1 2sin − cos 0 = 1 2[(0 + ) − (0 − 0)] = 2 . = 1 0 1 2(sin)2 = 1 2 · 1 2 0 1 2(1 − cos 2) = 1 8 − 1 2 sin 2 0 = 1 8[( − 0) − (0 − 0)] = 8 ≈ 039. Thus, the centroid is ( ) = ( 2 8 ). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 27 29. = 01(12 − 2) = 2 332 − 1 331 0 = 2 3 − 1 3 − 0 = 1 3 . = 1 01 (12 − 2) = 301(32 − 3) = 3 2 552 − 1 441 0 = 3 2 5 − 1 4 = 3 20 3 = 20 9 . = 1 01 1 2 (12)2 − (2)2 = 3 1 2 01( − 4) = 3 2 1 22 − 1 551 0 = 3 2 1 2 − 1 5 = 3 2 10 3 = 20 9 . Thus, the centroid is ( ) = 20 9 20 9 . 30. The curves intersect when 2 − 2 = ⇔ 0 = 2 + − 2 ⇔ 0 = ( + 2)( − 1) ⇔ = −2 or = 1. = −12(2 − 2 − ) = 2 − 1 33 − 1 221 −2 = 7 6 − − 10 3 = 9 2 . = 1 −12 (2 − 2 − ) = 2 9 −12(2 − 3 − 2) = 2 9 2 − 1 44 − 1 331 −2 = 2 9 12 5 − 8 3 = − 1 2 . = 1 −12 1 2[(2 − 2)2 − 2] = 2 9 · 1 2 −12(4 − 52 + 4) = 1 9 4 − 5 33 + 1 551 −2 = 1 9 38 15 − − 16 15 = 2 5 . Thus, the centroid is ( ) = (− 1 2 2 5). 31. = 04(cos − sin) = sin + cos 0 4 = √2 − 1. = −1 04 (cos − sin) = −1(sin + cos) + cos − sin 0 4 [integration by parts] = −1 4 √2 − 1 = 1 4 √2 − 1 √2 − 1 . = −1 04 1 2(cos2 − sin2 ) = 21 04 cos 2 = 41sin 2 0 4 = 41 = 4√21− 1. Thus, the centroid is ( ) = 4√√22−−14 4√21− 1 ≈ (027060). 32. = 01 3 + 12(2 − ) = 1 441 0 + 2 − 1 222 1 = 1 4 + (4 − 2) − 2 − 1 2 = 3 4 . = 1 01 (3) + 12 (2 − ) = 4 3 01 4 + 12(2 − 2) = 4 3 1 551 0 + 2 − 1 332 1 = 4 3 1 5 + 4 − 8 3 − 1 − 1 3 = 4 3 13 15 = 52 45 . [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.28 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION = 1 01 1 2(3)2 + 12 1 2(2 − )2 = 2 3 01 6 + 12( − 2)2 = 2 3 1 7 71 0 + 1 3( − 2)32 1 = 2 3 1 7 − 0 + 0 + 1 3 = 2 3 10 21 = 20 63 . Thus, the centroid is ( ) = 52 45 20 63 . 33. The curves intersect when 2 − = 2 ⇔ 0 = 2 + − 2 ⇔ 0 = ( + 2)( − 1) ⇔ = −2 or = 1. = −12(2 − − 2) = 2 − 1 2 2 − 1 331 −2 = 7 6 − − 10 3 = 9 2 . = 1 −12 1 2[(2 − )2 − (2)2] = 2 9 · 1 2 −12(4 − 4 + 2 − 4) = 1 9 4 − 22 + 1 33 − 1 5 51 −2 = 1 9 32 15 − − 184 15 = 8 5 . = 1 −12 (2 − − 2) = 2 9 −12(2 − 2 − 3) = 2 9 2 − 1 33 − 1 4 41 −2 = 2 9 12 5 − 8 3 = − 1 2 . Thus, the centroid is ( ) = ( 8 5 − 1 2). 34. An equation of the line is = − 3 2 + 3. = 1 2(2)(3) = 3, so = = 4(3) = 12. = 02 1 2 − 3 2 + 32 = 1 2 02 9 4 2 − 9 + 9 = 1 2(4) 3 4 3 − 9 2 2 + 92 0 = 2(6 − 18 + 18) = 12. = 02 − 3 2 + 3 = 02 − 3 2 2 + 3 = 4− 1 23 + 3 2 22 0 = 4(−4 + 6) = 8. = = 8 12 = 2 3 and = = 12 12 = 1. Thus, the center of mass is ( ) = 2 3 1. Since is constant, the center of mass is also the centroid. 35. The quarter-circle has equation = √42 − 2 for 0 ≤ ≤ 4 and the line has equation = −2. = 1 4 (4)2 + 2(4) = 4 + 8 = 4( + 2), so = = 6 · 4( + 2) = 24( + 2). = 04 1 2 √16 − 2 2 − (−2)2 = 1 2 04 (16 − 2 − 4) = 1 2(6)12 − 1 3 34 0 = 348 − 64 3 = 80. = 04 √16 − 2 − (−2) = 04 √16 − 2 + 04 2 = 6− 1 3(16 − 2)324 0 + 624 0 = 60 + 64 3 + 6(16) = 224. = = 224 24( + 2) = 28 3( + 2) and = = 24(80+ 2) = 3(10 + 2). Thus, the center of mass is 3(28 + 2) 3(10 + 2) ≈ (182065). 36. We’ll use = 8, so ∆ = − = 8 − 0 8 = 1. = 08 () ≈ 10 = 1 3[(0) + 4(1) + 2(2) + 4(3) + 2(4) + 4(5) + 2(6) + 4(7) + (8)] ≈ 1 3[0 + 4(20) + 2(26) + 4(23) + 2(22) + 4(33) + 2(40) + 4(32) + 0] = 1 3 (608) = 2026 or 304 15 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 29 Now 08 () ≈ 1 3[0 · (0) + 4 · 1 · (1) + 2 · 2 · (2) + 4 · 3 · (3) + 2 · 4 · (4) + 4 · 5 · (5) + 2 · 6 · (6) + 4 · 7 · (7) + 8 · (8)] ≈ 1 3[0 + 8 + 104 + 276 + 176 + 66 + 48 + 896 + 0] = 1 3 (2672) = 8906 or 1336 15 , so = 1 08 () ≈ 439. Also, 08 [()]2 ≈ 1 3[02 + 4(20)2 + 2(26)2 + 4(23)2 + 2(22)2 + 4(33)2 + 2(40)2 + 4(32)2 + 02] = 1 3 (17688) = 5896, so = 1 08 1 2[()]2 ≈ 145. Thus, the centroid is ( ) ≈ (44 15). 37. = −11[(3 − ) − (2 − 1)] = −11(1 − 2) odd-degree terms drop out = 201(1 − 2) = 2 − 1 331 0 = 2 2 3 = 4 3. = 1 −11 (3 − − 2 + 1) = 3 4 −11(4 − 2 − 3 + ) = 3 4 −11(4 − 2) = 3 4 · 201(4 − 2) = 3 2 1 55 − 1 331 0 = 3 2 − 15 2 = − 1 5. = 1 −11 1 2[(3 − )2 − (2 − 1)2] = 3 4 · 1 2 −11(6 − 24 + 2 − 4 + 22 − 1) = 3 8 · 201(6 − 34 + 32 − 1) = 3 4 1 77 − 3 55 + 3 − 1 0 = 3 4 − 16 35 = − 12 35. Thus, the centroid is ( ) = − 1 5 − 12 35 . 38. The curves intersect at = ≈ −1315974 and = ≈ 053727445. = [(2 − 2) − ] = 2 − 1 33 − ≈ 1452014. = 1 (2 − 2 − ) = 1 2 − 1 44 − + ≈ −0374293 = 1 1 2[(2 − 2)2 − ()2] = 21 (4 − 42 + 4 − 2) = 1 2 4 − 4 33 + 1 55 − 1 22 ≈ 1218131 Thus, the centroid is ( ) ≈ (−037122). 39. Choose - and -axes so that the base (one side of the triangle) lies along the -axis with the other vertex along the positive -axis as shown. From geometry, we know the medians intersect at a point 2 3 of the way from each vertex (along the median) to the opposite side. The median from goes to the midpoint 1 2( + ) 0 of side , so the point of intersection of the medians is 2 3 · 1 2( + ) 1 3 = 1 3( + ) 1 3. This can also be verified by finding the equations of two medians, and solving them simultaneously to find their point of intersection. Now let us compute the location of the centroid of the triangle. The area is = 1 2( − ). [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.30 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION = 1 0 · ( − ) + 0 · ( − ) = 1 0( − 2) + 0 − 2 = 212 − 1330 + 1 22 − 133 0 = −123 + 1 33 + 123 − 133 = 2 ( − ) · −3 6 + 2 ( − ) · 3 6 = 1 3( − )(2 − 2) = +3 and = 1 0 1 2 ( − )2 + 0 1 2( − )2 = 1 222 0(2 − 2 + 2) + 222 0(2 − 2 + 2) = 1 2222 − 2 + 1 330 + 2222 − 2 + 1 33 0 = 1 222−3 + 3 − 1 33 + 2223 − 3 + 1 33 = 162 (− + ) = ( −2 ) · ( −6)2 = 3 Thus, the centroid is ( ) = +3 3 , as claimed. Remarks: Actually the computation of is all that is needed. By considering each side of the triangle in turn to be the base, we see that the centroid is 1 3 of the way from each side to the opposite vertex and must therefore be the intersection of the medians. The computation of in this problem (and many others) can be simplified by using horizontal rather than vertical approximating rectangles. If the length of a thin rectangle at coordinate is (), then its area is ()∆, its mass is ()∆, and its moment about the -axis is ∆ = ()∆. Thus, = () and = () = 1 () In this problem, () = − ( − ) by similar triangles, so = 1 0 − ( − ) = 22 0( − 2) = 22 1 22 − 1 33 0 = 22 · 63 = 3 Notice that only one integral is needed when this method is used. 40. The rectangle to the left of the -axis has centroid − 1 2 1 and area 2. The triangle to the right of the -axis has area 2 and centroid 2 3 2 3 [by Exercise 39, the centroid is two-thirds of the way from the vertex (00) to the point (11)]. = = 1 2 =1 = 1 2 + 2 2− 1 2 + 2 2 3 = 1 4 1 3 = 12 1 . = = 1 2 =1 = 1 2 + 2 2(1) + 2 2 3 = 1 4 10 3 = 5 6 . Thus, the centroid is ( ) = 12 1 5 6. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 31 41. Divide the lamina into two triangles and one rectangle with respective masses of 2, 2 and 4, so that the total mass is 8. Using the result of Exercise 39, the triangles have centroids −1 2 3 and 1 2 3 . The centroid of the rectangle (its center) is 0 − 1 2 . So, using Formulas 5 and 7, we have = = 1 3 =1 = 1 8 2 2 3 + 2 2 3 + 4− 1 2 = 1 8 2 3 = 12 1 , and = 0, since the lamina is symmetric about the line = 0. Thus, the centroid is ( ) = 0 12 1 . 42. The parabola has equation = 2 and passes through ( ), so = 2 ⇒ = 2 and hence, = 2 2. R1 has area 1 = 0 2 2 = 2 1 33 0 = 2 33 = 13. Since R has area , R2 has area 2 = − 1 3 = 2 3. For R1: 1 = 1 1 0 2 2 = 3 2 0 3 = 33 1 44 0 = 33 1 44 = 34 1 = 1 1 0 1 22 22 = 3 224 0 4 = 235 1 55 0 = 235 1 55 = 10 3 Thus, the centroid for R1 is (1 1) = 3 4 10 3 . For R2: 2 = 1 2 0 − 2 2 = 23 0 − 12 3 = 231 22 − 412 4 0 = 3 222 − 42 = 2342 = 38 2 = 1 2 0 1 2()2 − 2 22 = 23 12 0 2 1 − 14 4 = 43 − 514 5 0 = 3 4 − 15 = 43 45 = 35 Thus, the centroid for R2 is (2 2) = 3 8 3 5. Note the relationships: 2 = 21, 1 = 22, 2 = 21. 43. ( + )() = () + () = () + () = + () [by (8)] = () + () = ( + ) () 44. A sphere can be generated by rotating a semicircle about its diameter. The center of mass travels a distance 2 = 2 34 [from Example 4] = 83 , so by the Theorem of Pappus, the volume of the sphere is = = 2 2 · 8 3 = 4 3 3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.32 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 45. A cone of height and radius can be generated by rotating a right triangle about one of its legs as shown. By Exercise 39, = 1 3, so by the Theorem of Pappus, the volume of the cone is = = 1 2 · base · height · (2) = 1 2 · 2 1 3 = 1 32. 46. From the symmetry in the figure, = 4. So the distance traveled by the centroid when rotating the triangle about the -axis is = 2 · 4 = 8. The area of the triangle is = 1 2 = 1 2(2)(3) = 3. By the Theorem of Pappus, the volume of the resulting solid is = 3(8) = 24. 47. The curve is the quarter-circle = √16 − 2, 0 ≤ ≤ 4. Its length is 1 4(2 · 4) = 2. Now 0 = 1 2(16 − 2)−12(−2) = √16−− 2 ⇒ 1 + (0)2 = 1 + 16−2 2 = 1616 − 2 ⇒ = 1 + (0)2 = √164− 2 so = 1 = 21 04 4(16 − 2)−12 = 24 −(16 − 2)124 0 = 2 (0 + 4) = 8 and = 1 = 21 04 16 − 2 · √164− 2 = 24 04 = 2 4 0 = 2 (4 − 0) = 8 . Thus, the centroid is 8 8 . Note that the centroid does not lie on the curve, but does lie on the line = , as expected, due to the symmetry of the curve. 48. (a) From Exercise 47, we have = (1) ⇔ = . The surface area is = 2 = 2 = 2() = (2), which is the product of the arc length of and the distance traveled by the centroid of . (b) From Exercise 47, = 2 and = 8 . By the Second Theorem of Pappus, the surface area is = (2) = 2(2 · 8 ) = 32. A geometric formula for the surface area of a half-sphere is = 22. With = 4, we get = 32, which agrees with our first answer. 49. The circle has arc length (circumference) = 2. As in Example 7, the distance traveled by the centroid during a rotation is = 2. Therefore, by the Second Theorem of Pappus, the surface area is = = (2)(2) = 42 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.3 APPLICATIONS TO PHYSICS AND ENGINEERING ¤ 33 50. (a) Let 0 ≤ ≤ 1. If , then ; that is, raising to a larger power produces a smaller number. (b) Using Formulas 9 and the fact that the area of R is = 01( − ) = 1 + 1 − 1 + 1 = − ( + 1)( + 1), we get = ( + 1)( + 1) − 01 [ − ] = ( + 1)( + 1) − 01+1 − +1 = ( + 1)( + 1) − + 2 1 − 1+ 2 = (( + 1)( + 2)( + 1) + 2) and = ( + 1)( + 1) − 01 1 2 ()2 − ()2 = ( + 1)( + 1) 2( − ) 012 − 2 = ( + 1)( + 1) 2( − ) 21+ 1 − 21+ 1 = (2( + 1)( + 1)(2+ 1) + 1) (c) If we take = 3 and = 4, then ( ) = 45 ·· 56 47 ·· 59 = 2 3 20 63 which lies outside R since 2 3 3 = 27 8 20 63. This is the simplest of many possibilities. 51. Suppose the region lies between two curves = () and = () where () ≥ (), as illustrated in Figure 13. Choose points with = 0 1 · · · = and choose ∗ to be the midpoint of the th subinterval; that is, ∗ = = 1 2(−1 + ). Then the centroid of the th approximating rectangle is its center = 1 2[() + ()]. Its area is [() − ()] ∆, so its mass is [() − ()] ∆. Thus, () = [() − ()]∆ · = [() − ()] ∆ and () = [() − ()] ∆ · 1 2[() + ()] = · 1 2 ()2 − ()2 ∆. Summing over and taking the limit as → ∞, we get = lim →∞ [() − ()] ∆ = [() − ()] and = lim →∞ · 1 2 ()2 − ()2 ∆ = 1 2 ()2 − ()2 . Thus, = = = 1 [() − ()] and = = = 1 1 2 ()2 − ()2 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.34 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION DISCOVERY PROJECT Complementary Coffee Cups 1. Cup A has volume = 0 [()]2 and cup B has volume = 0 [ − ()]2 = 0 {2 − 2() + [()]2} = 2 0 − 2 0 () + 0 [()]2 = 2 − 21 + Thus, = ⇔ ( − 21) = 0 ⇔ = 2(1); that is, is twice the average value of on the interval [0 ]. 2. From Problem 1, = ⇔ = 21 ⇔ 1 + 2 = 21 ⇔ 2 = 1. 3. Let 1 and 2 denote the x-coordinates of the centroids of 1 and 2, respectively. By Pappus’s Theorem, = 211 and = 2( − 2)2, so = ⇔ 11 = 2 − 22 ⇔ 2 = 11 + 22 (⇔) 2 = 1 2 (1 + 2) ⇔ 1 22 = 1 21 ⇔ 2 = 1, as shown in Problem 2. [ () The sum of the moments of the regions of areas 1 and 2 about the y-axis equals the moment of the entire -by- rectangle about the y-axis.] So, since 1 + 2 = , we have = ⇔ 1 = 2 ⇔ 1 = 1 2(1 + 2) ⇔ 1 = 1 2() ⇔ = 2(1), as shown in Problem 1. 4. We’ll use a cup that is = 8 cm high with a diameter of 6 cm on the top and the bottom and symmetrically bulging to a diameter of 8 cm in the middle (all inside dimensions). For an equation, we’ll use a parabola with a vertex at (44); that is, = ( − 4)2 + 4. To find , use the point (30): 3 = (0 − 4)2 + 4 ⇒ −1 = 16 ⇒ = − 16 1 . To find , we’ll use the relationship in Problem 1, so we need 1. 1 = 08 − 16 1 ( − 4)2 + 4 = −44 − 16 1 2 + 4 = − 4 = 204 − 16 1 2 + 4 = 2− 48 1 3 + 44 0 = 2− 4 3 + 16 = 88 3 Thus, = 2(1) = 2 8883 = 22 3 . So with = 8 and curve = − 1 16( − 4)2 + 4, we have = 08 − 16 1 ( − 4)2 + 42 = −44 − 16 1 2 + 42 = − 4 = 2 04 256 1 4 − 1 22 + 16 = 2 1280 1 5 − 1 63 + 164 0 = 2 4 5 − 32 3 + 64 = 2 812 15 = 1624 15 This is approximately 340 cm3 or 115 fl oz. And with = 22 3 , we know from Problem 1 that cup B holds the same amount. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.4 APPLICATIONS TO ECONOMICS AND BIOLOGY ¤ 35 8.4 Applications to Economics and Biology 1. By the Net Change Theorem, (4000) − (0) = 04000 0() ⇒ (4000) = 18,000 + 04000(082 − 0000 03 + 0000 000 0032) = 18,000 + 082 − 0000 0152 + 0000 000 00134000 0 = 18,000 + 3104 = $21,104 2. By the Net Change Theorem, (10,000) − (5000) = 5000 10,000 0() = 5000 10,000(48 − 00012) = 48 − 00006210 5000 ,000 = 420,000 − 225,000 = $195,000 3. By the Net Change Theorem, (50) − (0) = 050(06 + 0008) ⇒ (50) = 100 + 06 + 0004250 0 = 100 + (40 − 0) = 140, or $140,000. Similarly, (100) − (50) = 06 + 00042100 50 = 100 − 40 = 60, or $60,000. 4. Consumer surplus = 0400 [() − (400)] = 0400[(2000 − 46√) − 1080] = 0400(920 − 46√) = 460400(20 − 12) = 4620 − 2 332400 0 = 468000 − 2 3 · 8000 = 46 · 1 3 · 8000 ≈ $122,66667 5. () = 10 ⇒ 450 + 8 = 10 ⇒ + 8 = 45 ⇒ = 37. Consumer surplus = 037 [() − 10] = 037450 + 8 − 10 = 450 ln ( + 8) − 1037 0 = (450 ln 45 − 370) − 450 ln 8 = 450 ln 45 8 − 370 ≈ $40725 6. () = 3 + 0012. = (10) = 3 + 1 = 4. Producer surplus = 010[ − ()] = 010 4 − 3 − 0012 = − 0301310 0 ≈ 10 − 333 = $667 7. = () ⇒ 625 = 125 + 00022 ⇒ 500 = 500 1 2 ⇒ 2 = 5002 ⇒ = 500. Producer surplus = 0500[ − ()] = 0500[625 − (125 + 00022)] = 0500 500 − 500 1 2 = 500 − 1500 1 3500 0 = 5002 − 1500 1 (5003) ≈ $166,66667 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.36 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 8. (a) Demand curve () = supply curve () ⇔ 50 − 20 1 = 20 + 10 1 ⇔ 30 = 20 3 ⇔ = 200. (200) = 50 − 20 1 (200) = 40, so the market for this good is in equilibrium when the quantity is 200 and the price is $40. (b) At equilibrium, the Consumer surplus = 0200[() − 40] = 0200 50 − 20 1 − 40 = 10 − 40 1 2200 0 = $1000 and the Producer surplus = 0200[40 − ()] = 0200 40 − 20 − 10 1 = 20 − 20 1 2200 0 = $2000 9. (a) Demand function () = supply function () ⇔ 2284 − 18 = 27 + 574 ⇔ 171 = 45 ⇔ = 19 5 [38 thousand]. (38) = 2284 − 18(38) = 160. The market for the stereos is in equilibrium when the quantity is 3800 and the price is $160. (b) Consumer surplus = 038[() − 160] = 038(2284 − 18 − 160) = 038(684 − 18) = 684 − 923 08 = 684(38) − 9(38)2 = 12996 Producer surplus = 038[160 − ()] = 038[160 − (27 + 574)] = 038(1026 − 27) = 1026 − 13523 08 = 1026(38) − 135(38)2 = 19494 Thus, the maximum total surplus for the stereos is 12996 + 19494 = 3249, or $324,900. 10. () = () ⇔ 312−014 = 2602 ⇔ 312 26 = 02 −014 ⇔ 12 = 034 ⇔ ln 12 = 034 ⇔ = = ln 12 034 . ≈ 73085 (in thousands) and () ≈ 1121465. Consumer surplus = 0[() − ()] ≈ 073085(312−014 − 1121465) ≈ 607896 Producer surplus = 0[() − ()] ≈ 073085(1121465 − 2602) ≈ 388896 Maximum total surplus ≈ 607896 + 388896 = 996792, or $996,792. Note: Since () = (), the maximum total surplus could be found by calculating 0[() − ()] . 11. () = 800,000−5000 + 20,000 = 16 ⇒ = 1 ≈ 372704. Consumer surplus = 01[() − 16] ≈ $37,753 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.4 APPLICATIONS TO ECONOMICS AND BIOLOGY ¤ 37 12. The demand function is linear with slope −50 05 = − 100 1 and (500) = 10, so an equation is − 10 = − 100 1 ( − 500) or = − 100 1 + 15. A selling price of $8 implies that 8 = − 100 1 + 15 ⇒ 100 1 = 7 ⇒ = 700. Consumer surplus = 0700 − 100 1 + 15 − 8 = − 200 1 2 + 7700 0 = $2450. 13. (8) − (4) = 48 0() = 48 √ = 2 3 328 4 = 2 3 16√2 − 8 ≈ $975 million 14. The total revenue obtained in the first four years is = 04 () = 04 9000√1 + 2 = 19 900012 1 2 [ = 1 + 2, = 2 ] = 4500 2 3 329 1 = 3000(27 − 1) = $78,000 15. Future value = 0 ()(−) = 06 8000004 0062(6−) = 800006 004 0372−0062 = 800006 0372−0022 = 80000372 06 −0022 = 80000372 −−00022 022 6 0 = 80000372 −0022 (−0132 − 1) ≈ $65,23048 16. Present value = 0 ()− = 06 8000004 −0062 = 800006 −0022 = 8000−−00022 022 6 0 = 8000 −0022 (−0132 − 1) ≈ $44,96691 17. = − = −−+ 1 +1 = 1 − (1− − 1−). Similarly, 1− = 22−− = 2 − (2− − 2−). Thus, = 1 1− = [[ (2 (1 −− )]( )](2 1− − − − 2 1− − ) ) = (1 (2 − − )( )( 2 1− − − − 2 1− − ) ). 18. (9) − (5) = 59(2200 + 1008) = 2200 + 100088 9 5 = 22009 5 + 25 2 089 5 = 2200(9 − 5) + 125(72 − 4) ≈ 24,860 19. = 4 8 = (4000)(0008)4 8(0027)(2) ≈ 119 × 10−4 cm3s 20. If the flux remains constant, then 004 8 = 4 8 ⇒ 004 = 4 ⇒ 0 = 0 4. = 3 4 0 ⇒ 0 = 3 400 4 ⇒ = 0 4 3 4 ≈ 316050 30; that is, the blood pressure is more than tripled. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.38 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 21. From (3), = 0 () = 206 , where = 010 −06 = (−016)2 (−06 − 1)−0610 0 integrating by parts = 0136(−7−6 + 1) Thus, = 6(036) 20(1 − 7−6) = 0108 1 − 7−6 ≈ 01099 Ls or 6594 Lmin. 22. As in Example 2, we will estimate the cardiac output using Simpson’s Rule with ∆ = (16 − 0)8 = 2. 016 () ≈ 2 3[(0) + 4(2) + 2(4) + 4(6) + 2(8) + 4(10) + 2(12) + 4(14) + (16)] = 2 3 [0 + 4(41) + 2(89) + 4(85) + 2(67) + 4(43) + 2(25) + 4(12) + 02] = 2 3 (1088) = 7253 mg · s/L Therefore, ≈ 7253 = 55 7253 ≈ 00758 Ls or 455 Lmin. 23. As in Example 2, we will estimate the cardiac output using Simpson’s Rule with ∆ = (16 − 0)8 = 2. 016 () ≈ 2 3[(0) + 4(2) + 2(4) + 4(6) + 2(8) + 4(10) + 2(12) + 4(14) + (16)] ≈ 2 3[0 + 4(61) + 2(74) + 4(67) + 2(54) + 4(41) + 2(30) + 4(21) + 15] = 2 3 (1091) = 7273 mg· sL Therefore, ≈ 7273 = 7 7273 ≈ 00962 Ls or 577 Lmin. 8.5 Probability 1. (a) 30 40,000 ,000 () is the probability that a randomly chosen tire will have a lifetime between 30,000 and 40,000 miles. (b) 25 ∞,000 () is the probability that a randomly chosen tire will have a lifetime of at least 25,000 miles. 2. (a) The probability that you drive to school in less than 15 minutes is 015 (). (b) The probability that it takes you more than half an hour to get to school is 30 ∞ (). 3. (a) In general, we must satisfy the two conditions that are mentioned before Example 1 — namely, (1) () ≥ 0 for all , and (2) −∞ ∞ () = 1. For 0 ≤ ≤ 1, () = 302(1 − )2 ≥ 0 and () = 0 for all other values of , so () ≥ 0 for all . Also, −∞ ∞ () = 01 302(1 − )2 = 01 302(1 − 2 + 2) = 01(302 − 603 + 304) = 103 − 154 + 651 0 = 10 − 15 + 6 = 1 Therefore, is a probability density function. (b) ≤ 1 3 = −∞ 13 () = 013 302(1 − )2 = 103 − 154 + 651 03 = 10 27 − 15 81 + 243 6 = 17 81 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.5 PROBABILITY ¤ 39 4. (a) In general, we must satisfy the two conditions that are mentioned before Example 1 — namely, (1) () ≥ 0 for all , and (2) −∞ ∞ () = 1. For () = 3− (1 + 3−)2 , the numerator and denominator are both positive, so () ≥ 0 for all . Also, −∞ ∞ () = −∞ 0 () + 0∞ () = lim →−∞ 0 (1 +3−3−)2 + lim →∞ 0 (1 +3−3−)2 = lim →−∞ 0= − 2 + lim →∞ =0 − 2 = 1 + = −3−3− = lim →−∞ 10 = + lim →∞ 1 =0 = lim →−∞ 1 +13− 0 + lim →∞ 1 +13− 0 = lim →−∞ 1 +13 − 1 +13− + lim →∞ 1 +13− − 1 +13 = 1 +13 − 0 + 1 − 1 +13 = 1. Therefore, is a probability density function. (b) (3 ≤ ≤ 4) = 34 () = 1 +13− 4 3 [from part (a)] = 1 +1−1 − 1 + 1 1 ≈ 0231 (c) The graph of appears to be symmetric about the line = 3, so the mean appears to be 3. Similarly, half the area under the graph of appears to lie to the right of = 3, so the median also appears to be 3. 5. (a) In general, we must satisfy the two conditions that are mentioned before Example 1—namely, (1) () ≥ 0 for all , and (2) −∞ ∞ () = 1. If ≥ 0, then () ≥ 0, so condition (1) is satisfied. For condition (2), we see that −∞ ∞ () = −∞ ∞ 1 + 2 and Similarly, 0∞ 1 + 2 = lim →∞ 0 1 + 2 = lim →∞ tan−1 0 = lim →∞tan−1 = 2 −∞ 0 1 + 2 = 2 , so −∞ ∞ 1 + 2 = 2 2 = . Since must equal 1, we must have = 1 so that is a probability density function. (b) (−1 1) = −11 1 + 12 = 2 01 1 +12 = 2 tan−1 1 0 = 2 4 − 0 = 12 6. (a) For 0 ≤ ≤ 3, we have () = (3 − 2), which is nonnegative if and only if ≥ 0. Also, −∞ ∞ () = 03 (3 − 2) = 3 2 2 − 1 3 33 0 = 27 2 − 9 = 9 2 . Now 9 2 = 1 ⇒ = 2 9. Therefore, is a probability density function if and only if = 2 9. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.40 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION (b) Let = 2 9. ( 1) = 1∞ () = 13 29(3 − 2) = 2 9 3 22 − 1 333 1 = 2 9 27 2 − 9 − 3 2 − 1 3 = 2 9 10 3 = 20 27. (c) The mean = −∞ ∞ () = 03 2 9(3 − 2) = 2 9 03(32 − 3) = 2 9 3 − 1 443 0 = 2 9 27 − 81 4 = 2 9 27 4 = 3 2. 7. (a) In general, we must satisfy the two conditions that are mentioned before Example 1—namely, (1) () ≥ 0 for all , and (2) −∞ ∞ () = 1. Since () = 0 or () = 01, condition (1) is satisfied. For condition (2), we see that −∞ ∞ () = 010 01 = 10 1 10 0 = 1. Thus, () is a probability density function for the spinner’s values. (b) Since all the numbers between 0 and 10 are equally likely to be selected, we expect the mean to be halfway between the endpoints of the interval; that is, = 5. = −∞ ∞ () = 010 (01) = 20 1 210 0 = 100 20 = 5, as expected. 8. (a) As in the preceding exercise, (1) () ≥ 0 and (2) −∞ ∞ () = 010 () = 1 2(10)(02) [area of a triangle] = 1. So () is a probability density function. (b) (i) ( 3) = 03 () = 1 2(3)(01) = 20 3 = 015 (ii) We first compute ( 8) and then subtract that value and our answer in (i) from 1 (the total probability). ( 8) = 810 () = 1 2(2)(01) = 20 2 = 010. So (3 ≤ ≤ 8) = 1 − 015 − 010 = 075. (c) We find equations of the lines from (00) to (6 02) and from (6 02) to (100), and find that () = 1 30 if 0 ≤ 6 − 1 20 + 1 2 if 6 ≤ 10 0 otherwise = −∞ ∞ () = 06 30 1 + 610 − 20 1 + 1 2 = 90 1 36 0 + − 60 1 3 + 1 4210 6 = 216 90 + − 1000 60 + 100 4 − − 216 60 + 36 4 = 16 3 = 53 9. We need to find so that ∞ () = 1 2 ⇒ lim →∞ 1 5−5 = 1 2 ⇒ lim →∞ 1 5(−5)−5 = 1 2 ⇒ (−1)(0 − −5) = 1 2 ⇒ −5 = 1 2 ⇒ −5 = ln 1 2 ⇒ = −5ln 1 2 = 5 ln 2 ≈ 347 min. 10. (a) = 1000 ⇒ () = 01000 1 −1000 if if ≥ 00 (i) (0 ≤ ≤ 200) = 0200 1000 1 −1000 = −−1000200 0 = −−15 + 1 ≈ 0181 (ii) ( 800) = 800 ∞ 1000 1 −1000 = lim →∞−−1000 800 = 0 + −45 ≈ 0449 (b) We need to find so that ∞ () = 1 2 ⇒ lim →∞ 1000 1 −1000 = 1 2 ⇒ lim →∞−−1000 = 1 2 ⇒ 0 + −1000 = 1 2 ⇒ −1000 = ln 1 2 ⇒ = −1000 ln 1 2 = 1000 ln 2 ≈ 6931 h. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.5 PROBABILITY ¤ 41 11. (a) An exponential density function with = 16 is () = 0116−16 if if ≥ 00. The probability that a customer waits less than a second is ( 1) = 01 () = 01 116−16 = −−161 0 = −−116 + 1 ≈ 0465. (b) The probability that a customer waits more than 3 seconds is ( 3) = 3∞ () = lim →∞ 3 () = lim →∞ −−16 3 = lim →∞(−−16 + −316) = −316 ≈ 0153. Or: Calculate 1 − 03 (). (c) We want to find such that ( ) = 005. From part (b), ( ) = −16. Solving −16 = 005 gives us − 16 = ln005 ⇒ = −16ln005 ≈ 479 seconds. Or: Solve 0 () = 095 for . 12. (a) We first find an antiderivative of () = 2 . 2 = 1 2 − 2 == 2 2 , , == 1 = 1 2 − 2 1 − 1 == , , == 1 = 1 2 − 2 2 + 23 + = 1 2 − 2 + 22 + = −20−005(2 + 40 + 800) + [with = −005] (0 ≤ ≤ 48) = 048 () = 15,1676 048 () = 15,1676−20−005(2 + 40 + 800)48 0 = −20 15,676(5024−24 − 800) ≈ 0439. (b) ( 36) = (36 ≤ 150) = 1 15,676 36 150 () = 15,1676−20−005(2 + 40 + 800)150 36 = −20 15,676(29,300−75 − 3536−18) ≈ 0725 13. (a) () = 1 1600 if 0 ≤ ≤ 40 1 20 − 1 1600 if 40 ≤ 80 0 otherwise (30 ≤ ≤ 60) = 3060 () = 3040 1600 + 4060 20 1 − 1600 = 3200 2 40 30 + 20 − 3200 2 60 40 = 3200 1600 − 3200 900 + 60 20 − 3600 3200 − 40 20 − 1600 3200 = −1300 3200 + 1 = 19 32 The probability that the amount of REM sleep is between 30 and 60 minutes is 19 32 ≈ 594%. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.42 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION (b) = −∞ ∞ () = 040 1600 + 4080 20 1 − 1600 = 4800 3 40 0 + 40 2 − 4800 3 80 40 = 64,000 4800 + 6400 40 − 512 4800 ,000 − 1600 40 − 64 4800 ,000 = −384 4800 ,000 + 120 = 40 The mean amount of REM sleep is 40 minutes. 14. (a) With = 69 and = 28, we have (65 ≤ ≤ 73) = 6573 28√1 2 exp−(2−· 269) 82 2 ≈ 0847 (using a calculator or computer to estimate the integral). (b) ( 6 feet) = ( 72 inches) = 1 − (0 ≤ ≤ 72) ≈ 1 − 0858 = 0142, so 142% of the adult male population is more than 6 feet tall. 15. ( ≥ 10) = 10∞ 421 √2 exp−(2−· 4924) 2 2 . To avoid the improper integral we approximate it by the integral from 10 to 100. Thus, ( ≥ 10) ≈ 10100 42√1 2 exp−(2−· 4924) 2 2 ≈ 0443 (using a calculator or computer to estimate the integral), so about 44 percent of the households throw out at least 10 lb of paper a week. Note: We can’t evaluate 1 − (0 ≤ ≤ 10) for this problem since a significant amount of area lies to the left of = 0. 16. (a) (0 ≤ ≤ 480) = 0480 12√1 2 exp−(2−· 12 500) 2 2 ≈ 00478 (using a calculator or computer to estimate the integral), so there is about a 478% chance that a particular box contains less than 480 g of cereal. (b) We need to find so that (0 ≤ 500) = 005. Using our calculator or computer to find (0 ≤ ≤ 500) for various values of , we find that if = 51973, = 005007; and if = 51974, = 004998. So a good target weight is at least 51974 g. 17. (a) (0 ≤ ≤ 100) = 0100 8√12 exp−( −2 ·112) 82 2 ≈ 00668 (using a calculator or computer to estimate the integral), so there is about a 668% chance that a randomly chosen vehicle is traveling at a legal speed. (b) ( ≥ 125) = 125 ∞ 8√12 exp−( 2−·112) 82 2 = 125 ∞ (). In this case, we could use a calculator or computer to estimate either 125 300 () or 1 − 0125 (). Both are approximately 00521, so about 521% of the motorists are targeted. 18. () = 1 √2 −(−)2(22) ⇒ 0() = √12 −(−)2(22) −2(2−2 ) = 3−√12 −(−)2(22)( − ) ⇒ 00() = −1 3 √2 −(−)2(22) · 1 + ( − )−(−)2(22) −2(2−2 ) = −1 3 √2 −(−)2(22) 1 − ( −2)2 = 5 √1 2 −(−)2(22) ( − )2 − 2 00() 0 ⇒ ( − )2 − 2 0 ⇒ | − | ⇒ − − ⇒ − + and similarly, 00() 0 ⇒ − or + . Thus, changes concavity and has inflection points at = ± . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 8.5 PROBABILITY ¤ 43 19. ( − 2 ≤ ≤ + 2) = −+2 2 √12 exp−(2−2)2 . Substituting = − and = 1 gives us −22 √12 − 2/2( ) = √12 −22 − 2/2 ≈ 09545. 20. Let () = 0 − if if ≥ 00 where = 1. By using parts, tables, or a CAS, we find that (1): = (2)( − 1) (2): 2 = (3)(22 − 2 + 2) Now 2 = −∞ ∞ ( − )2() = −∞ 0 ( − )2() + 0∞( − )2() = 0 + lim →∞ 0( − )2− = · lim →∞ 02− − 2− + 2− Next we use (2) and (1) with = − to get 2 = lim →∞ −−3 22 + 2 + 2 − 2−2 (− − 1) + 2 −− 0 Using l’Hospital’s Rule several times, along with the fact that = 1, we get 2 = 0 − −23 + 2 · 12 + 12 · −1 = 13 = 12 ⇒ = 1 = 21. (a) First () = 4 3 0 2−20 ≥ 0 for ≥ 0. Next, −∞ ∞ () = 0∞ 43 0 2−20 = 43 0 lim →∞ 0 2−20 By using parts, tables, or a CAS [or as in Exercise 20] , we find that 2 = (3)(22 − 2 + 2). () Next, we use () (with = −20) and l’Hospital’s Rule to get 4 3 0 −3 08(−2) = 1. This satisfies the second condition for a function to be a probability density function. (b) Using l’Hospital’s Rule, 4 3 0 lim →∞ 2 20 = 4 30 lim →∞ 2 (20)20 = 2 20 lim →∞ 2 (20)20 = 0. To find the maximum of , we differentiate: 0() = 4 3 0 2−20−20 + −20(2) = 43 0 −20(2)−0 + 1 0() = 0 ⇔ = 0 or 1 = 0 ⇔ = 0 [0 ≈ 559 × 10−11 m]. 0() changes from positive to negative at = 0, so () has its maximum value at = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.44 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION (c) It is fairly difficult to find a viewing rectangle, but knowing the maximum value from part (b) helps. (0) = 4 3 0 2 0−200 = 4 0 −2 ≈ 9,684,098,979 With a maximum of nearly 10 billion and a total area under the curve of 1, we know that the “hump” in the graph must be extremely narrow. (d) () = 0 43 0 2−20 ⇒ (40) = 040 43 0 2−20 . Using () from part (a) [with = −20], (40) = 4 3 0 −−82 3 00 42 0 2 + 40 + 24 00 = 43 0 −3 08[−8(64 + 16 + 2) − 1(2)] = − 1 2(82−8 − 2) = 1 − 41−8 ≈ 0986 (e) = −∞ ∞ () = 43 0 lim →∞ 0 3−20 . Integrating by parts three times or using a CAS, we find that 3 = 4 33 − 322 + 6 − 6. So with = −20 , we use l’Hospital’s Rule, and get = 4 30 −16 4 0 (−6) = 3 2 0. 8 Review 1. = 4( − 1)32 ⇒ = 6( − 1)12 ⇒ 1 + 2 = 1 + 36( − 1) = 36 − 35. Thus, = 14 √36 − 35 = 1109 √( 36 1 ) = 36 = 36 − 35, = 1 36 2 3 32109 1 = 54 1 (109√109 − 1) 2. = 2 lnsin 1 2 ⇒ = 2 · sin11 2 · cos 1 2 · 1 2 = cot 1 2 ⇒ 1 + 2 = 1 + cot2 1 2 = csc2 1 2 . Thus, = 3 csc2 1 2 = 3 csc 1 2 = 3 csc 1 2 = 62 csc(2) == 1 21 2 = 2ln|csc − cot| 2 6 = 2ln csc 2 − cot 2 − ln csc 6 − cot 6 = 2ln|1 − 0| − ln 2 − √3 = −2ln2 − √3 ≈ 263 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 8 REVIEW ¤ 45 3. 12 = 43 + 3−1 ⇒ = 1 33 + 1 4−1 ⇒ = 2 − 1 4−2 ⇒ 1 + 2 = 1 + 4 − 1 2 + 16 1 −4 = 4 + 1 2 + 16 1 −4 = (2 + 1 4−2)2. Thus, = 13 2 + 1 4−22 = 13 2 + 1 4−2 = 13 2 + 1 4−2 = 1 33 − 1 4−13 1 = (9 − 12 1 ) − ( 1 3 − 1 4) = 106 12 = 53 6 4. (a) = 4 16 + 1 22 = 1 16 4 + 1 2 −2 ⇒ = 1 4 3 − −3 ⇒ 1 + ()2 = 1 + 1 43 − −32 = 1 + 16 1 6 − 1 2 + −6 = 16 1 6 + 1 2 + −6 = 1 43 + −32. Thus, = 12 1 43 + −3 = 16 1 4 − 1 2−22 1 = 1 − 1 8 − 16 1 − 1 2 = 21 16 . (b) = 12 2 1 43 + −3 = 2 12 1 44 + −2 = 2 20 1 5 − 1 2 1 = 2 32 20 − 1 2 − 20 1 − 1 = 2 8 5 − 1 2 − 20 1 + 1 = 2 41 20 = 41 10 5. (a) = 2 + 1 ⇒ 0 = −2 ( + 1)2 ⇒ 1 + (0)2 = 1 + ( + 1) 4 4 . For 0 ≤ ≤ 3, = 03 1 + (0)2 = 03 1 + 4( + 1)4 ≈ 35121. (b) The area of the surface obtained by rotating about the -axis is = 03 2 = 2 03 + 1 2 1 + 4( + 1)4 ≈ 221391. (c) The area of the surface obtained by rotating about the -axis is = 03 2 = 2 03 1 + 4( + 1)4 ≈ 298522. 6. (a) = 2 ⇒ 1 + (0)2 = 1 + 42. Rotate about the -axis for 0 ≤ ≤ 1: = 01 2 √1 + 42 = 15 4 √ [ = 1 + 42] = 6 325 1 = 6 (532 − 1) (b) = 2 ⇒ 1 + (0)2 = 1 + 42. Rotate about the -axis for 0 ≤ ≤ 1: = 2 01 2 √1 + 42 = 2 02 1 42 √1 + 2 1 2 [ = 2] = 4 02 2 √1 + 2 = 4 1 8(1 + 22)√1 + 2 − 1 8 ln + √1 + 2 2 0 [ = tan or use Formula 22] = 4 1 4(9)√5 − 1 8 ln2 + √5 − 0 = 32 18√5 − ln2 + √5 7. = sin ⇒ 0 = cos ⇒ 1 + (0)2 = 1 + cos2 . Let () = √1 + cos2 . Then = 0 () ≈ 10 = ( − 0)10 3 (0) + 4 10 + 2 210 + 4 310 + 2 410 + 4 510 + 2 610 + 4 710 + 2 810 + 4 910 + () ≈ 3820188 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.46 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 8. = 0 2 = 0 2 sin √1 + cos2 . Let () = 2 sin √1 + cos2 . Then = 0 () ≈ 10 = ( − 0)10 3 (0) + 4 10 + 2 210 + 4 310 + 2 410 + 4 510 + 2 610 + 4 710 + 2 810 + 4 910 + () ≈ 14426045 9. = 1 √ − 1 ⇒ = √ − 1 ⇒ 1 + ()2 = 1 + √ − 1 = √. Thus, = 116 √ = 116 14 = 4 5 5416 1 = 4 5(32 − 1) = 124 5 . 10. = 116 2 = 2 116 · 14 = 2 116 54 = 2 · 4 9 9416 1 = 89(512 − 1) = 4088 9 11. As in Example 8.3.1, 2 − = 1 2 ⇒ 2 = 2 − and = 2(15 + ) = 3 + 2 = 3 + 2 − = 5 − . Thus, = 02 (5 − ) = 5 22 − 1 332 0 = 10 − 8 3 = 22 3 ≈ 458 lb [ ≈ 625 lbft3]. 12. = 04 (4 − )22√ = 4 04(412 − 32) = 4 8 332 − 2 5524 0 = 4 64 3 − 64 5 = 256 1 3 − 1 5 = 512 15 ≈ 21333 lb [ ≈ 625 lbft3] 13. = 04 √ − 1 2 = 2 332 − 1 424 0 = 16 3 − 4 = 4 3 = 1 04 √ − 1 2 = 3 4 04 32 − 1 22 = 3 4 2 552 − 1 634 0 = 3 4 64 5 − 64 6 = 3 4 64 30 = 8 5 = 1 04 1 2 √ 2 − 1 22 = 3 4 04 1 2 − 1 42 = 3 8 1 22 − 12 1 34 0 = 3 8 8 − 16 3 = 3 8 8 3 = 1 Thus, the centroid is ( ) = 8 5 1. 14. From the symmetry of the region, = 2 . = 3 4 4 sin = −cos3 44 = √12 − − √12 = √2 = 1 3 4 4 1 2 sin2 = 1 3 4 4 1 4 (1 − cos 2) = 1 4√2 − 1 2 sin 23 44 = 1 4√2 34 − 1 2 (−1) − 4 + 1 2 · 1 = 4√1 2 2 + 1 Thus, the centroid is ( ) = 2 4√1 2 2 + 1 ≈ (157 045). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 8 REVIEW ¤ 47 15. The area of the triangular region is = 1 2(2)(4) = 4. An equation of the line is = 1 2 or = 2. = 1 02 1 2[()]2 = 14 02 1 2(2)2 = 18 02 42 = 184332 0 = 16(8) = 43 = 1 02 () = 14 02 (2) = 12 02 2 = 121332 0 = 16(8) = 4 3 The centroid of the region is 4 3 43. 16. An equation of the line is = 8 − . An equation of the quarter-circle is = −√82 − 2 with 0 ≤ ≤ 8. The area of the region is = 1 2(8)(8) + 1 4(8)2 = 32 + 16 = 16(2 + ). = 1 08 [() − ()] = 1 08 (8 − ) + 64 − 2 = 1 08 8 − 2 + (64 − 2)12 = 1 42 − 133 − 1 3(64 − 2)328 0 = 1 256 − 512 3 − 0 − 0 − 0 − 512 3 = 16(2 + 256 ) = 2 + 16 = 1 08 1 2{[()]2 − [()]2} = 21 08 (8 − )2 − (−64 − 2 )2 = 1 2 08 64 − 16 + 2 − (64 − 2) = 21 08(22 − 16) = 1 08(2 − 8) = 1 1 33 − 428 0 = 1 512 3 − 256 = 1 16(2 + ) −256 3 = −3(2 + 16 ) The centroid of the region is 2 + 16 −3(2 + 16 ) ≈ (311 −104). 17. The centroid of this circle, (1 0), travels a distance 2(1) when the lamina is rotated about the -axis. The area of the circle is (1)2. So by the Theorem of Pappus, = (2) = (1)22(1) = 22. 18. The semicircular region has an area of 1 22, and sweeps out a sphere of radius when rotated about the -axis. = 0 because of symmetry about the line = 0. And by the Theorem of Pappus, = (2) ⇒ 4 3 3 = 1 22(2) ⇒ = 34 . Thus, the centroid is ( ) = 0 34. 19. = 100 ⇒ = 2000 − 01(100) − 001(100)2 = 1890 Consumer surplus = 0100[() − ] = 01002000 − 01 − 0012 − 1890 = 110 − 0052 − 03013100 0 = 11,000 − 500 − 10,3000 ≈ $716667 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.48 ¤ CHAPTER 8 FURTHER APPLICATIONS OF INTEGRATION 20. 024 () ≈ 12 = 24 12−· 30[1(0) + 4(19) + 2(33) + 4(51) + 2(76) + 4(71) + 2(58) + 4(47) + 2(33) + 4(21) + 2(11) + 4(05) + 1(0)] = 2 3 (1278) = 852 mg · sL Therefore, ≈ 852 = 6852 ≈ 00704 Ls or 4225 Lmin. 21. () = 020 sin 10 if if 0 ≤ 0 or ≤ 10 10 (a) () ≥ 0 for all real numbers and −∞ ∞ () = 010 20 sin 10 = 20 · 10 −cos 10 10 0 = 1 2(−cos + cos 0) = 1 2(1 + 1) = 1 Therefore, is a probability density function. (b) ( 4) = −∞ 4 () = 04 20 sin 10 = 1 2 −cos 10 4 0 = 1 2 −cos 25 + cos 0 ≈ 1 2(−0309017 + 1) ≈ 03455 (c) = −∞ ∞ () = 010 20 sin 10 = 0 20 · 10 (sin) 10 [ = 10 , = 10 ] = 5 0 sin =82 5 [sin − cos] 0 = 5 [0 − (−1)] = 5 This answer is expected because the graph of is symmetric about the line = 5. 22. (250 ≤ ≤ 280) = 250 280 √12 −(−)2(22) = 250 280 15√12 exp−(2 ·−15268) 2 2 ≈ 0673. Thus, the percentage of pregnancies that last between 250 and 280 days is about 673%. 23. (a) The probability density function is () = 01 8 −8 if if ≥ 00 (0 ≤ ≤ 3) = 03 18 −8 = −−83 0 = −−38 + 1 ≈ 03127 (b) ( 10) = 10 ∞ 1 8 −8 = lim →∞ −−8 10 = lim →∞(−−8 + −108) = 0 + −54 ≈ 02865 (c) We need to find such that ( ≥ ) = 1 2 ⇒ ∞ 1 8 −8 = 1 2 ⇒ lim →∞ −−8 = 1 2 ⇒ lim →∞ (−−8 + −8) = 1 2 ⇒ −8 = 1 2 ⇒ −8 = ln 1 2 ⇒ = −8ln 1 2 = 8 ln 2 ≈ 555 minutes. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.PROBLEMS PLUS 1. 2 + 2 ≤ 4 ⇔ 2 + ( − 2)2 ≤ 4, so is part of a circle, as shown in the diagram. The area of is 014 − 2 113 = −2 2 4 − 2 + 2 cos−1 2−2 1 0 [ = 2] = − 1 2 √3 + 2 cos−1 1 2 − 2cos−1 1 = − √3 2 + 2 3 − 2(0) = 23 − √23 Another method (without calculus): Note that = ∠ = 3 , so the area is (area of sector ) − (area of 4) = 1 2 22 3 − 1 2(1)√3 = 23 − √23 2. = ±√3 − 4 ⇒ The loop of the curve is symmetric about = 0, and therefore = 0. At each point where 0 ≤ ≤ 1, the lamina has a vertical length of √3 − 4 − −√3 − 4 = 2√3 − 4. Therefore, = 01 · 2√3 − 4 01 2√3 − 4 = 01 √3 − 4 01 √3 − 4 . We evaluate the integrals separately: 01 √3 − 4 = 0152√1 − = 022sin6 cos1 − sin2 sin =2 sin √,cos cos == (2√ ), = 022sin6 cos2 = 022 1 2 (1 − cos 2)3 1 2(1 + cos 2) = 02 1 8(1 − 2cos 2 + 2 cos3 2 − cos4 2) = 02 1 81 − 2cos 2 + 2 cos 2(1 − sin2 2) − 1 4(1 + cos 4)2 = 1 8 − 1 3 sin3 2 0 2 − 32 1 02 1 + 2 cos 4 + cos2 4 = 16 − 1 32 + 1 2 sin 4 0 2 − 64 1 02 (1 + cos 8) = 16 − 1 32 + 1 2 sin 4 0 2 − 64 1 02 (1 + cos 8) = 3 64 − 1 64 + 1 8 sin 8 0 2 = 128 5 01√3 − 4 = 0132√1 − = 022sin4 cos 1 − sin2 [sin = √ ] = 022sin4 cos2 = 022 · 1 4(1 − cos 2)2 · 1 2(1 + cos 2) = 02 1 4(1 − cos 2 − cos2 2 + cos3 2) = 02 1 41 − cos 2 − 1 2(1 + cos 4) + cos 2(1 − sin2 2) = 1 4 2 − 1 8 sin 4 − 1 6 sin3 2 0 2 = 16 Therefore, = 5128 16 = 5 8 , and ( ) = 5 80. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 49 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.50 ¤ CHAPTER 8 PROBLEMS PLUS 3. (a) The two spherical zones, whose surface areas we will call 1 and 2, are generated by rotation about the -axis of circular arcs, as indicated in the figure. The arcs are the upper and lower portions of the circle 2 + 2 = 2 that are obtained when the circle is cut with the line = . The portion of the upper arc in the first quadrant is sufficient to generate the upper spherical zone. That portion of the arc can be described by the relation = 2 − 2 for ≤ ≤ . Thus, = −2 − 2 and = 1 + 2 = 1 + 2 −2 2 = 2 −2 2 = 2 − 2 From Formula 8.2.8 we have 1 = 2 1 + 2 = 2 2 − 2 2 − 2 = 2 = 2( − ) Similarly, we can compute 2 = − 2 1 + ()2 = − 2 = 2( + ). Note that 1 + 2 = 42, the surface area of the entire sphere. (b) = 3960 mi and = (sin 75◦) ≈ 3825 mi, so the surface area of the Arctic Ocean is about 2(−) ≈ 2(3960)(135) ≈ 336×106 mi2. (c) The area on the sphere lies between planes = 1 and = 2, where 2 − 1 = . Thus, we compute the surface area on the sphere to be = 12 2 1 + 2 = 12 2 = 2(2 − 1) = 2. This equals the lateral area of a cylinder of radius and height , since such a cylinder is obtained by rotating the line = about the -axis, so the surface area of the cylinder between the planes = 1 and = 2 is = 12 2 1 + 2 = 12 2 1 + 02 = 2 2 =1 = 2(2 − 1) = 2 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 8 PROBLEMS PLUS ¤ 51 (d) = 2 sin2345◦ ≈ 3152 mi, so the surface area of the Torrid Zone is 2 ≈ 2(3960)(3152) ≈ 784 × 107 mi2. 4. (a) Since the right triangles and are similar, we have + = ⇒ = 2 + . The surface area visible from is = 2 1 + ()2 . From 2 + 2 = 2, we get (2 + 2) = (2) ⇒ 2 + 2 = 0 ⇒ = − and 1 + 2 = 2 +2 2 = 22 . Thus, = 2 · = 2( − ) = 2 − +2 = 221 − + = 22 · + = 2 +2 . (b) Assume ≥ . If a light is placed at point , at a distance from the center of the sphere of radius , then from part (a) we find that the total illuminated area on the two spheres is [with + = and + = − ]. () = 22( − ) + 22( − − ) − [ ≤ ≤ − ]. 2() = 21 − + 2 1 − − , so 0() = 0 ⇔ 0 = 2 · 2 + 2 · (−−)2 ⇔ 32 = ( −3)2 ⇔ ( −2)2 = 33 ⇔ − 12 = 3 ⇒ − 1 = 32 ⇔ = 1 + 32 ⇔ = ∗ = 1 + ( )32 . Now 0() = 232 − ( −3)2 ⇒ 00() = 2−233 − (2−3)3 and 00(∗) 0, so we have a local maximum at = ∗. However, ∗ may not be an allowable value of — we must show that ∗ is between and − . (1) ∗ ≥ ⇔ 1 + ()32 ≥ ⇔ ≥ + (2) ∗ ≤ − ⇔ 1 + ()32 ≤ − ⇔ ≤ − + 32 − 32 ⇔ + 32 ≤ 32 ⇔ ≥ ( )32 + = + , but + ≤ + , and since + [given], we conclude that ∗ ≤ − . [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.52 ¤ CHAPTER 8 PROBLEMS PLUS Thus, from (1) and (2), ∗ is not an allowable value of if + . So may have a maximum at = , ∗, or − . () = 22( − − ) − and ( − ) = 22(−− − ) () ( − ) ⇔ 2 − 2 − ⇔ 2( − ) 2( − ) ⇔ 2 − 3 2 − 3 ⇔ 2 − 2 3 − 3 ⇔ ( − )( + ) ( − )(2 + + 2) ⇔ (2 + + 2)( + ) ⇔ [( + )2 − ]( + ) ⇔ + − ( + ). Now + − ( + ) + , and we know that + , so we conclude that () ( − ). In conclusion, has an absolute maximum at = ∗ provided ≥ + ; otherwise, has its maximum at = 5. (a) Choose a vertical -axis pointing downward with its origin at the surface. In order to calculate the pressure at depth , consider subintervals of the interval [0 ] by points and choose a point ∗ ∈ [−1 ] for each . The thin layer of water lying between depth −1 and depth has a density of approximately (∗ ), so the weight of a piece of that layer with unit cross-sectional area is (∗ ) ∆. The total weight of a column of water extending from the surface to depth (with unit cross-sectional area) would be approximately =1 (∗ ) ∆. The estimate becomes exact if we take the limit as → ∞; weight (or force) per unit area at depth is = lim →∞ =1 (∗ ) ∆. In other words, () = 0 () . More generally, if we make no assumptions about the location of the origin, then () = 0 + 0 () , where 0 is the pressure at = 0. Differentiating, we get = (). (b) = − ( + ) · 2√2 − 2 = −0 + 0+ 0 · 2√2 − 2 = 0 − 2√2 − 2 + 0 −(+) − 1 · 2√2 − 2 = (0 − 0)− 2√2 − 2 + 0 − (+) · 2√2 − 2 = (0 − 0)2 + 0 − · 2√2 − 2 6. The problem can be reduced to finding the line which minimizes the shaded area in the diagram. An equation of the circle in the first quadrant is = 1 − 2. So the shaded area is () = 0 1 − 1 − 2 + 1 1 − 2 = 0 1 − 1 − 2 − 1 1 − 2 0() = 1 − √1 − 2 − √1 − 2 [by FTC] = 1 − 2√1 − 2 0 = 0 ⇔ √1 − 2 = 1 2 ⇒ 1 − 2 = 1 4 ⇒ 2 = 3 4 ⇒ = √23. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 8 PROBLEMS PLUS ¤ 53 00() = −2 · 1 2(1 − 2)−12(−2) = √12− 2 0, so = √23 gives a minimum value of . Note: Another strategy is to use the angle as the variable (see the diagram above) and show that = + cos − 4 − 1 2 sin2, which is minimized when = 6 . 7. To find the height of the pyramid, we use similar triangles. The first figure shows a cross-section of the pyramid passing through the top and through two opposite corners of the square base. Now || = , since it is a radius of the sphere, which has diameter 2 since it is tangent to the opposite sides of the square base. Also, || = since 4 is isosceles. So the height is || = √2 + 2 = √2. We first observe that the shared volume is equal to half the volume of the sphere, minus the sum of the four equal volumes (caps of the sphere) cut off by the triangular faces of the pyramid. See Exercise 6.2.49 for a derivation of the formula for the volume of a cap of a sphere. To use the formula, we need to find the perpendicular distance of each triangular face from the surface of the sphere. We first find the distance from the center of the sphere to one of the triangular faces. The third figure shows a cross-section of the pyramid through the top and through the midpoints of opposite sides of the square base. From similar triangles we find that = || || = √2 2 + √22 ⇒ = √22 √32 = √6 3 So = − = − √6 3 = 3 −3√6. So, using the formula = 2( − 3) from Exercise 6.2.49 with = , we find that the volume of each of the caps is 3 −3√62 − 3 3−·√3 6 = 15 −96√6 · 6 +9√63 = 2 3 − 27 7 √63. So, using our first observation, the shared volume is = 1 2 4 33 − 4 2 3 − 27 7 √63 = 28 27√6 − 23. 8. Orient the positive -axis as in the figure. Suppose that the plate has height and is symmetric about the -axis. At depth below the water (2 ≤ ≤ 2 + ), let the width of the plate be 2(). Now each of the horizontal strips has height and the th strip (1 ≤ ≤ ) goes from = 2 + − 1 to = 2 + . The hydrostatic force on the th strip is () = 2+[( 2+( −1)) ] 625[2()]. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.54 ¤ CHAPTER 8 PROBLEMS PLUS If we now let [2()] = (a constant) so that () = (2), then () = 2+[( 2+( −1)) ] 625 = 625 2+( 2+[( −1) )] = 6252 + − 2 + − 1 = 625 So the hydrostatic force on the th strip is independent of , that is, the force on each strip is the same. So the plate can be shaped as shown in the figure. (In fact, the required condition is satisfied whenever the plate has width at depth , for some constant . Many shapes are possible.) 9. We can assume that the cut is made along a vertical line = 0, that the disk’s boundary is the circle 2 + 2 = 1, and that the center of mass of the smaller piece (to the right of = ) is 1 20. We wish to find to two decimal places. We have 1 2 = = 1 · 2√1 − 2 12√1 − 2 . Evaluating the numerator gives us −1(1 − 2)12(−2) = − 2 31 − 2321 = − 2 30 − 1 − 232 = 2 3(1 − 2)32. Using Formula 30 in the table of integrals, we find that the denominator is √1 − 2 + sin−11 = 0 + 2 − √1 − 2 + sin−1. Thus, we have 12 = = 2 3(1 − 2)32 2 − √1 − 2 − sin−1, or, equivalently, 2 3(1 − 2)32 = 4 − 1 2 √1 − 2 − 1 2 sin−1. Solving this equation numerically with a calculator or CAS, we obtain ≈ 0138173, or = 014 m to two decimal places. 10. 1 = 30 ⇒ 1 2 = 30 ⇒ = 60. = 6 ⇒ 1 2 010 () = 6 ⇒ 0 + 10 − + 10 (10) = 6(70) ⇒ 0 2 + 10 − + 10 · 1 2210 = 420 ⇒ 33 + 52 − 22 0 + 5(100 − 2) = 420 ⇒ 1 32 + 52 − 1 22 + 500 − 52 = 420 ⇒ 80 = 1 62 ⇒ 480 = () ⇒ 480 = 60 ⇒ = 8. So = 60 8 = 15 2 and an equation of the line is = 152 8 + 10 − 15 2 = 15 16 + 52. Now = 1 2 010 1 2[()]2 = 701· 2 08 15 16 + 522 + 810(10)2 = 1 140 08 225 2562 + 75 16 + 25 4 + 100(10 − 8) = 140 1 225 7683 + 75 322 + 25 4 8 0 + 200 = 1 140(150 + 150 + 50 + 200) = 550 140 = 55 14 [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 8 PROBLEMS PLUS ¤ 55 Another solution: Assume that the right triangle cut from the square has legs cm and cm long as shown. The triangle has area 30 cm2, so 1 2 = 30 and = 60. We place the square in the first quadrant of the -plane as shown, and we let , , and denote the triangle, the remaining portion of the square, and the full square, respectively. By symmetry, the centroid of is (5 5). By Exercise 8.3.39, the centroid of is 3 10 − 3. We are given that the centroid of is (6 ), where is to be determined. We take the density of the square to be 1, so that areas can be used as masses. Then has mass = 30, has mass = 100, and has mass = − = 70. As in Exercises 40 and 41 of Section 8.3, we view as consisting of a mass at the centroid ( ) of and a mass at the centroid ( ) of . Then = + + and = + + ; that is, 5 = 30(3) + 70(6) 100 and 5 = 30(10 − 3) + 70 100 . Solving the first equation for , we get = 8 cm. Since = 60 cm2, it follows that = 60 8 = 75 cm. Now the second equation says that 70 = 200 + 10, so 7 = 20 + = 55 2 and = 55 14 = 39285714 cm. The solution is depicted in the figure. 11. If = , then = area under = sin area of rectangle = 0 sin = [−cos ] 0 = −(−1) + 1 = 2 . If = 2, then = area under = 1 2sin area of rectangle = 0 1 2sin = [−cos ] 0 2 = 2 2 = 1 . 12. (a) The total set of possibilities can be identified with the rectangular region R = {( ) | 0 ≤ 0 ≤ }. Even when , the needle intersects at least one line if and only if ≤ sin. Let R1 = {( ) | 0 ≤ ≤ sin0 ≤ }. When ≤ , R1 is contained in R, but that is no longer true when . Thus, the probability that the needle intersects a line becomes = area(R ∩ R1) area(R) = area(R ∩ R1) When , the curve = sin intersects the line = twice — at sin−1() and at − sin−1() . Set 1 = sin−1 () and 2 = − 1. Then °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.56 ¤ CHAPTER 8 PROBLEMS PLUS area(R ∩ R1) = 01 sin + 12 + 2 sin = 201 sin + (2 − 1) = 2 −cos 01 + ( − 21) = 2(1 − cos1) + ( − 21) = 21 − √2− 2 + − 2sin−1 = 2 − 2√2 − 2 + − 2sin−1 We are told that = 4 and = 7, so area(R ∩ R1) = 14 − 2√33 + 4 − 8sin−1 4 7 ≈ 1021128 and = 1 4 area(R ∩ R1) ≈ 0812588. (By comparison, = 2 ≈ 0636620 when = , as shown in the solution to Problem 11.) (b) The needle intersects at least two lines when + ≤ sin; that is, when ≤ sin − . Set R2 = {( ) | 0 ≤ ≤ sin − 0 ≤ }. Then the probability that the needle intersects at least two lines is 2 = area(R ∩ R2) area(R) = area(R ∩ R2) When = 4 and = 7, R2 is contained in R (see the figure). Thus, 2 = 1 4 area(R2) = 41 sin −−sin 1(4−7) 1(47)(7 sin − 4) = 41 · 2sin −21(47)(7 sin − 4) = 1 2 −7cos − 4 sin2−1(47) = 21 0 − 2 + 7√733 + 4 sin−1 4 7 = √33 + 4 sin2−1 4 7 − 2 ≈ 0301497 (c) The needle intersects at least three lines when + 2 ≤ sin: that is, when ≤ sin − 2. Set R3 = {( ) | 0 ≤ ≤ sin − 20 ≤ }. Then the probability that the needle intersects at least three lines is 3 = area(R ∩ R3) area(R) = area(R ∩ R3) . (At this point, the generalization to , any positive integer, should be clear.) Under the given assumption, 3 = 1 area(R3) = 1 sin −−sin 1(2− 1(2))(sin − 2) = 2 sin −21(2)(sin − 2) = 2 −cos − 2 sin2−1(2) = 2 − + √2 − 42 + 2sin−1(2) Note that the probability that a needle touches exactly one line is 1 − 2, the probability that it touches exactly two lines is 2 − 3, and so on. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 8 PROBLEMS PLUS ¤ 57 13. Solve for : 2 + ( + + 1)2 = 1 ⇒ ( + + 1)2 = 1 − 2 ⇒ + + 1 = ±√1 − 2 ⇒ = − − 1 ± √1 − 2. = −11 − − 1 + 1 − 2 − − − 1 − 1 − 2 = −11 21 − 2 = 2 2 semicircle area of = = 1 −11 · 21 − 2 = 0 [odd integrand] = 1 −11 1 2− − 1 + 1 − 2 2 − − − 1 − 1 − 2 2 = 1 −11 1 2−4 1 − 2 − 41 − 2 = − 2 −11 1 − 2 + 1 − 2 = −2 −11 1 − 2 − 2 −11 1 − 2 = − 2 (0) [odd integrand] − 2 2 semicircle area of = −1 Thus, as expected, the centroid is ( ) = (0 −1). We might expect this result since the centroid of an ellipse is located at its center. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.58 ¤ CHAPTER 8 PROBLEMS PLUS °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved. [Show More]
Last updated: 1 year ago
Preview 1 out of 2 pages
Instant download

Buy this document to get the full access instantly
Instant Download Access after purchase
Add to cartInstant download
Reviews( 0 )
Document information
Connected school, study & course
About the document
Uploaded On
Jan 06, 2020
Number of pages
2
Written in
Additional information
This document has been written for:
Uploaded
Jan 06, 2020
Downloads
0
Views
58