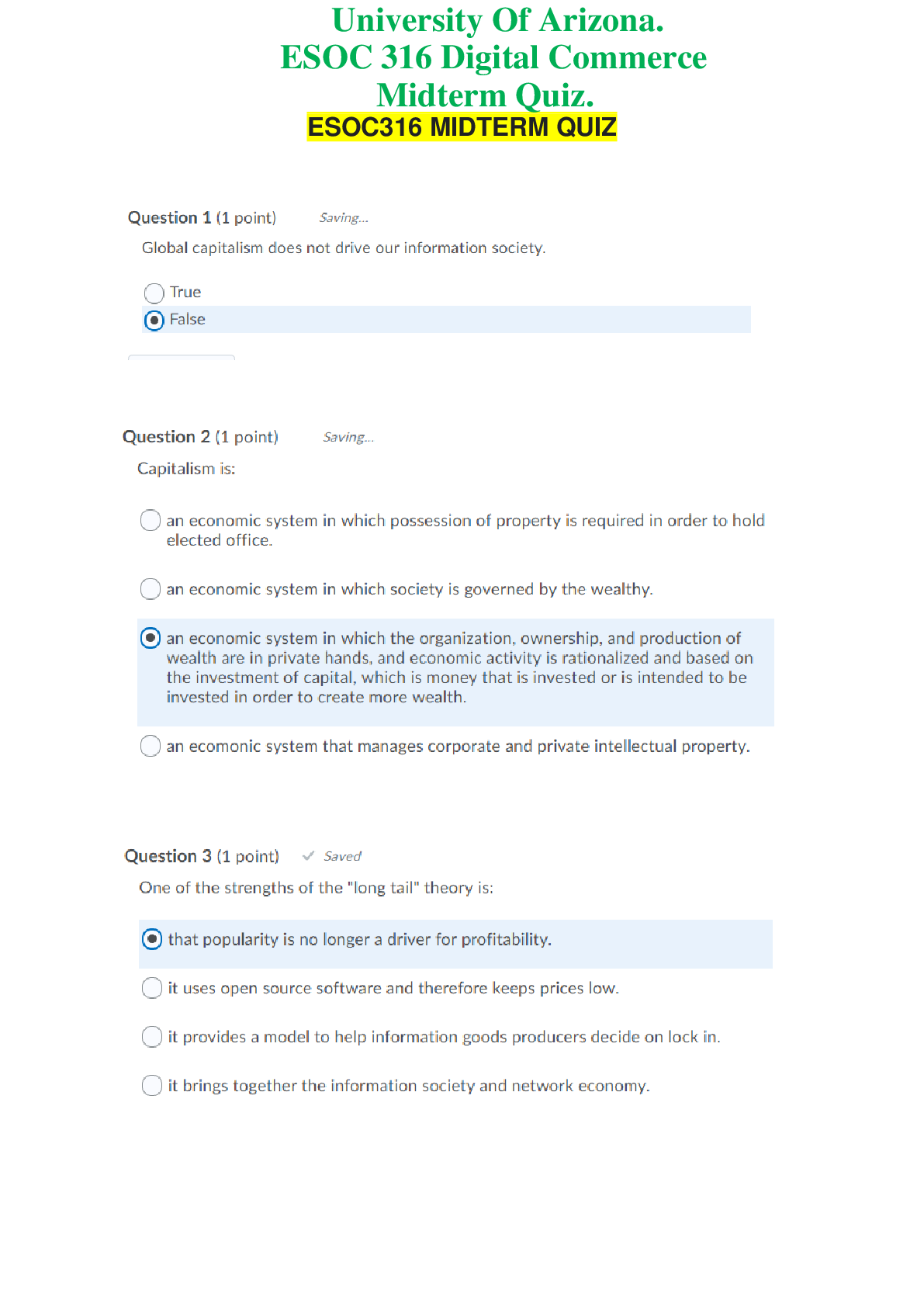
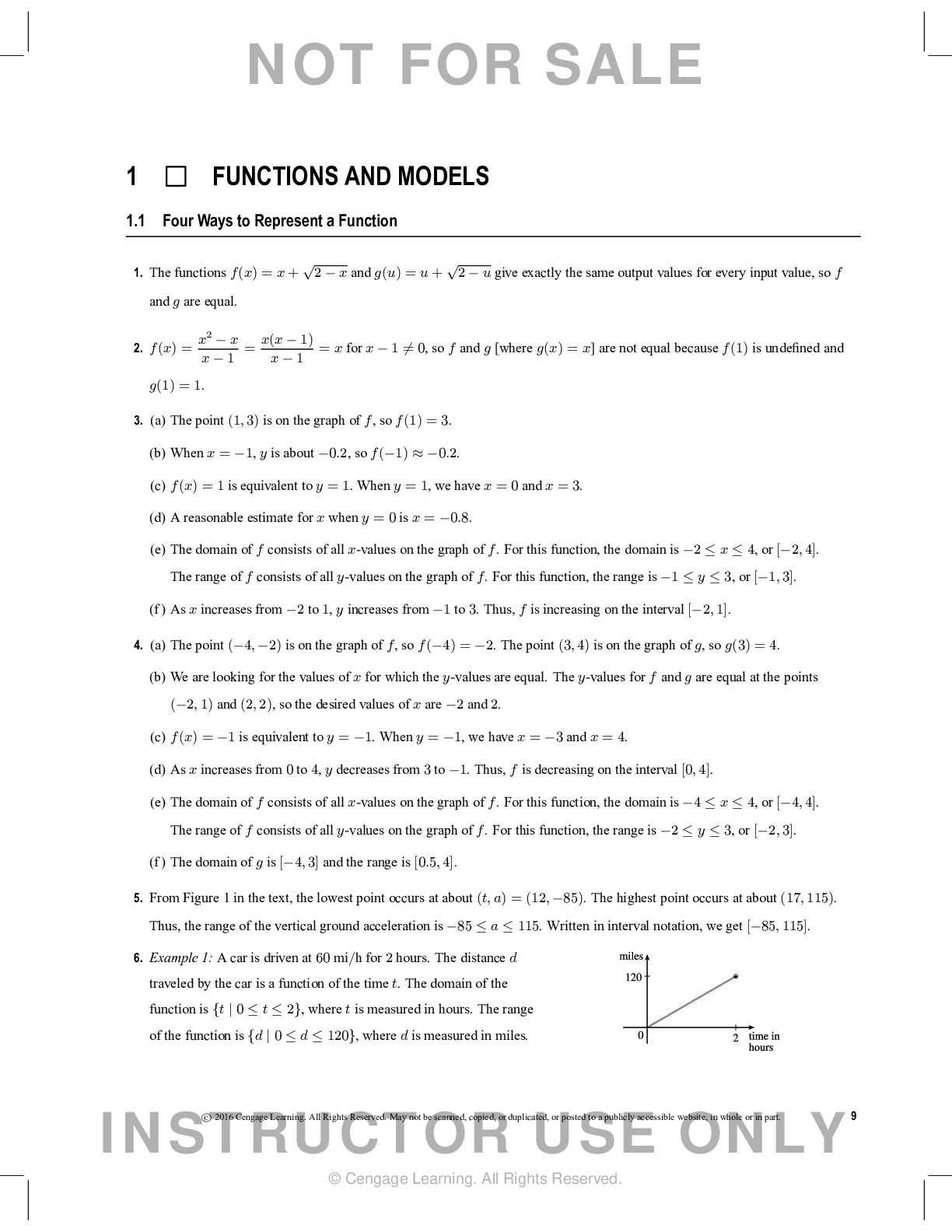
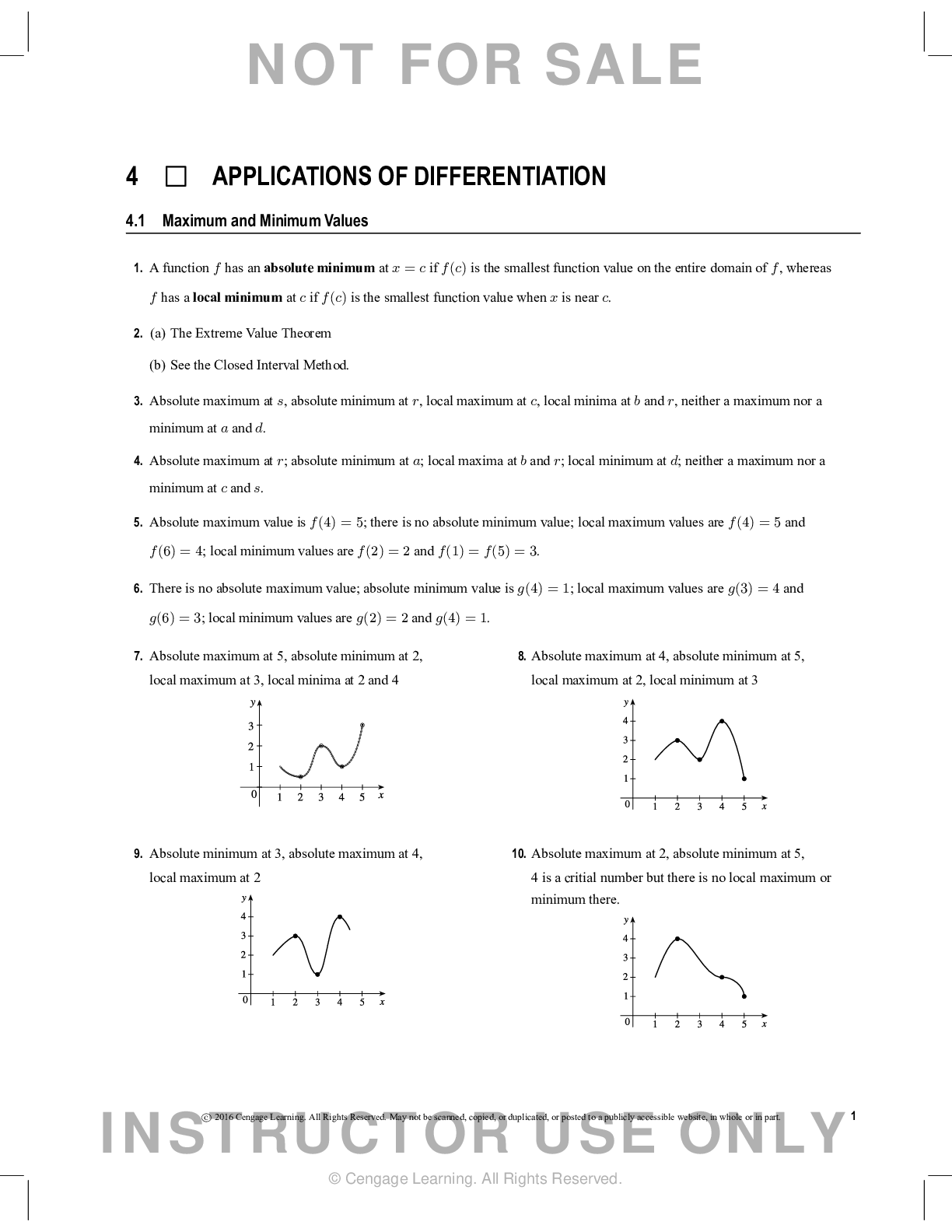
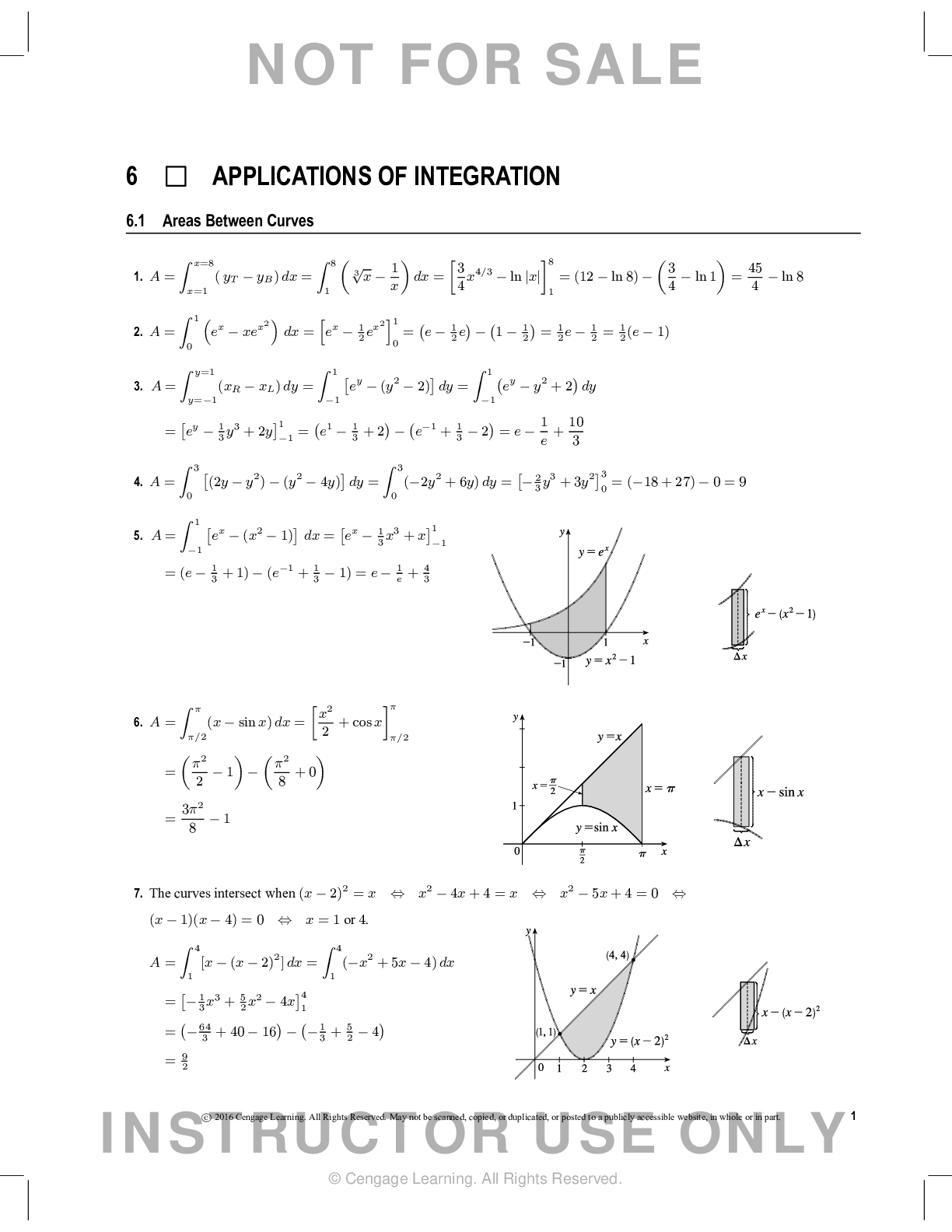
Calculus > QUESTIONS & ANSWERS > Chapter 12: VECTORS AND THE GEOMETRY OF SPACE. Work and Answers (All)
Chapter 12: VECTORS AND THE GEOMETRY OF SPACE. Work and Answers
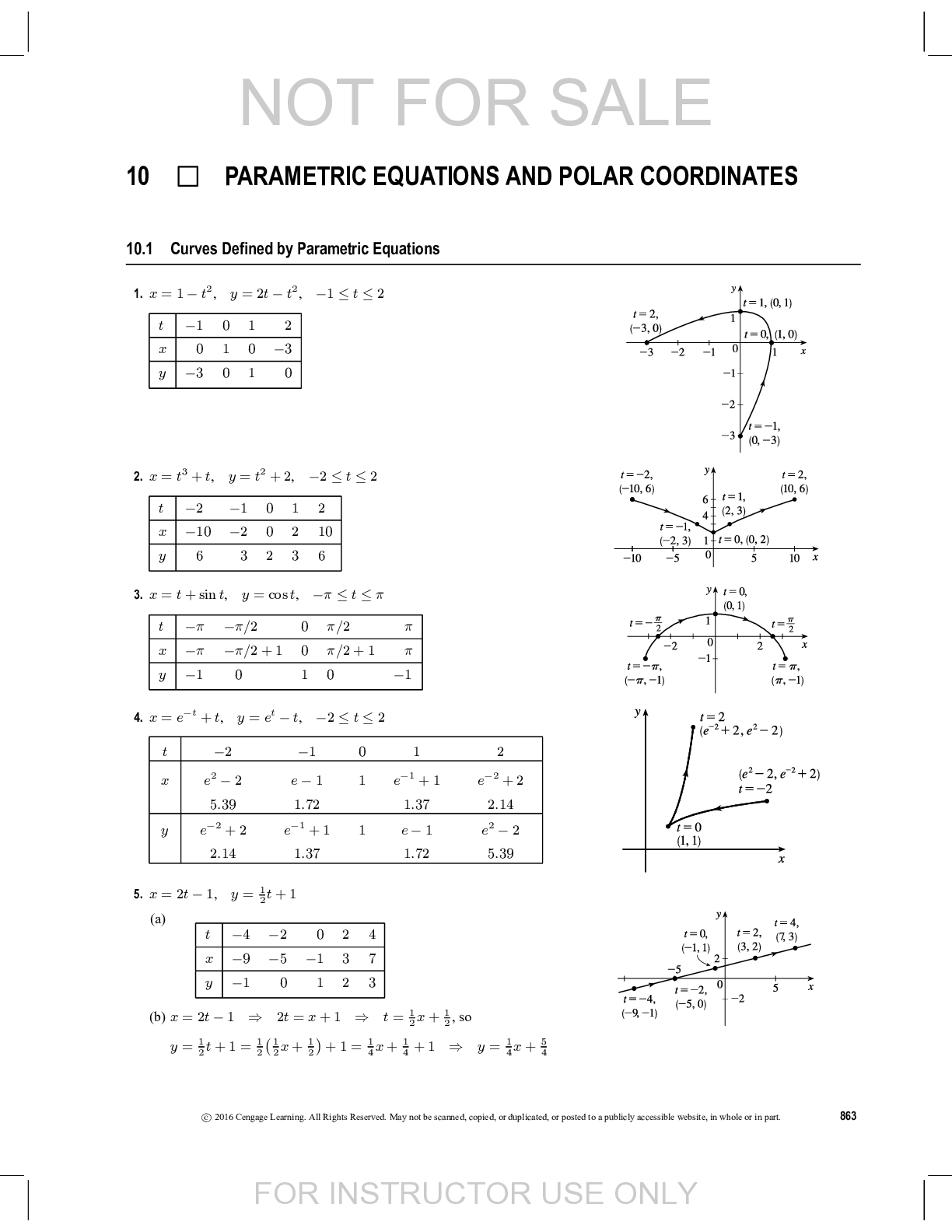
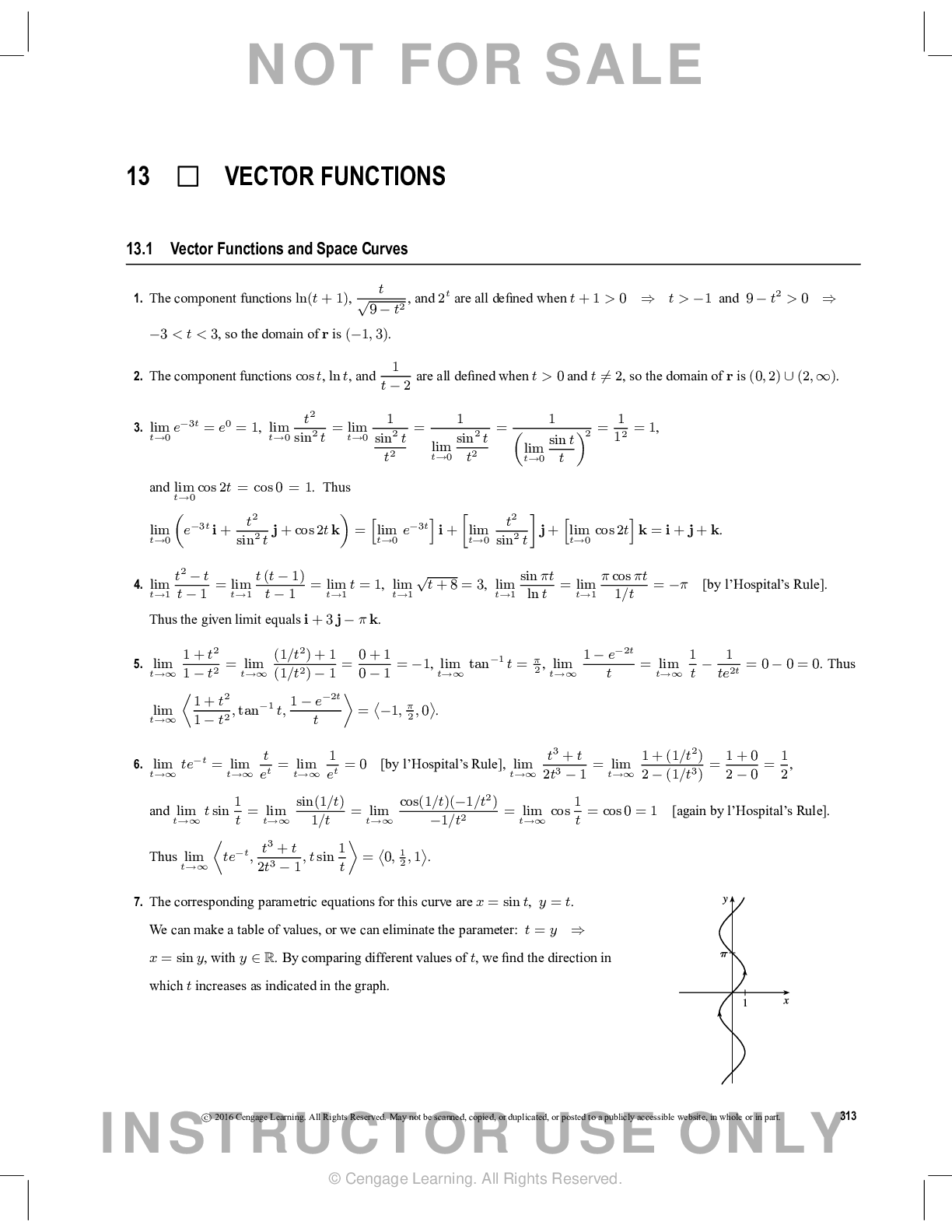
Document Content and Description Below
12.1 Three-Dimensional Coordinate Systems 1. We start at the origin, which has coordinates (0 0 0). First we move 4 units along the positive -axis, affecting only the -coordinate, bring... ing us to the point (400). We then move 3 units straight downward, in the negative -direction. Thus only the -coordinate is affected, and we arrive at (40 −3). 2. 3. The distance from a point to the -plane is the absolute value of the -coordinate of the point. (246) has the -coordinate with the smallest absolute value, so is the point closest to the -plane. (−40 −1) must lie in the -plane since the distance from to the -plane, given by the -coordinate of , is 0. 4. The projection of (235) onto the -plane is (230); onto the -plane, (035); onto the -plane, (205). The length of the diagonal of the box is the distance between the origin and (235), given by (2 − 0)2 + (3 − 0)2 + (5 − 0)2 = √38 ≈ 616 5. In R2, the equation = 4 represents a line parallel to the -axis and 4 units to the right of it. In R3, the equation = 4 represents the set {( ) | = 4}, the set of all points whose -coordinate is 4. This is the vertical plane that is parallel to the -plane and 4 units in front of it. 6. In R3, the equation = 3 represents a vertical plane that is parallel to the -plane and 3 units to the right of it. The equation = 5 represents a horizontal plane parallel to the -plane and 5 units above it. The pair of equations = 3, = 5 represents the set of points that are simultaneously on both planes, or in other words, the line of intersection of the planes = 3, = 5. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 1 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.2 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE This line can also be described as the set {(35) | ∈ R}, which is the set of all points in R3 whose -coordinate may vary but whose - and -coordinates are fixed at 3 and 5, respectively. Thus the line is parallel to the -axis and intersects the -plane in the point (0 3 5). 7. The equation + = 2 represents the set of all points in R3 whose - and -coordinates have a sum of 2, or equivalently where = 2 − This is the set {(2 − ) | ∈ R ∈ R} which is a vertical plane that intersects the -plane in the line = 2 − , = 0. 8. The equation 2 + 2 = 9 has no restrictions on , and the - and -coordinates satisfy the equation for a circle of radius 3 with center the origin. Thus the surface 2 + 2 = 9 in R3 consists of all possible vertical circles (parallel to the -plane) 2 + 2 = 9, = , and is therefore a circular cylinder with radius 3 whose axis is the -axis. 9. We can find the lengths of the sides of the triangle by using the distance formula between pairs of vertices: || = (7 − 3)2 + [0 − (−2)]2 + [1 − (−3)]2 = √16 + 4 + 16 = 6 || = (1 − 7)2 + (2 − 0)2 + (1 − 1)2 = √36 + 4 + 0 = √40 = 2√10 || = (3 − 1)2 + (−2 − 2)2 + (−3 − 1)2 = √4 + 16 + 16 = 6 The longest side is , but the Pythagorean Theorem is not satisfied: | |2 + ||2 6= ||2. Thus is not a right triangle. is isosceles, as two sides have the same length. 10. Compute the lengths of the sides of the triangle by using the distance formula between pairs of vertices: | | = (4 − 2)2 + [1 − (−1)]2 + (1 − 0)2 = √4 + 4 + 1 = 3 || = (4 − 4)2 + (−5 − 1)2 + (4 − 1)2 = √0 + 36 + 9 = √45 = 3√5 || = (2 − 4)2 + [−1 − (−5)]2 + (0 − 4)2 = √4 + 16 + 16 = 6 Since the Pythagorean Theorem is satisfied by ||2 + | |2 = ||2, is a right triangle. is not isosceles, as no two sides have the same length. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.1 THREE-DIMENSIONAL COORDINATE SYSTEMS ¤ 3 11. (a) First we find the distances between points: || = (3 − 2)2 + (7 − 4)2 + (−2 − 2)2 = √26 || = (1 − 3)2 + (3 − 7)2 + [3 − (−2)]2 = √45 = 3√5 || = (1 − 2)2 + (3 − 4)2 + (3 − 2)2 = √3 In order for the points to lie on a straight line, the sum of the two shortest distances must be equal to the longest distance. Since √26 + √3 6= 3√5, the three points do not lie on a straight line. (b) First we find the distances between points: || = (1 − 0)2 + [−2 − (−5)]2 + (4 − 5)2 = √11 || = (3 − 1)2 + [4 − (−2)]2 + (2 − 4)2 = √44 = 2√11 || = (3 − 0)2 + [4 − (−5)]2 + (2 − 5)2 = √99 = 3√11 Since || + || = ||, the three points lie on a straight line. 12. (a) The distance from a point to the -plane is the absolute value of the -coordinate of the point. Thus, the distance is |6| = 6. (b) Similarly, the distance to the -plane is the absolute value of the -coordinate of the point: |4| = 4. (c) The distance to the -plane is the absolute value of the -coordinate of the point: |−2| = 2. (d) The point on the -axis closest to (4 −26) is the point (4 0 0). (Approach the -axis perpendicularly.) The distance from (4 −26) to the -axis is the distance between these two points: (4 − 4)2 + (−2 − 0)2 + (6 − 0)2 = √40 = 2√10 ≈ 632. (e) The point on the -axis closest to (4 −2 6) is (0 −20). The distance between these points is (4 − 0)2 + [−2 − (−2)]2 + (6 − 0)2 = √52 = 2√13 ≈ 721. (f) The point on the -axis closest to (4 −26) is (00 6). The distance between these points is (4 − 0)2 + (−2 − 0)2 + (6 − 6)2 = √20 = 2√5 ≈ 447. 13. An equation of the sphere with center (−325) and radius 4 is [ − (−3)]2 + ( − 2)2 + ( − 5)2 = 42 or ( + 3)2 + ( − 2)2 + ( − 5)2 = 16. The intersection of this sphere with the -plane is the set of points on the sphere whose -coordinate is 0. Putting = 0 into the equation, we have 9 + ( − 2)2 + ( − 5)2 = 16 = 0 or ( − 2)2 + ( − 5)2 = 7 = 0, which represents a circle in the -plane with center (025) and radius √7. 14. An equation of the sphere with center (2 −64) and radius 5 is ( − 2)2 + [ − (−6)]2 + ( − 4)2 = 52 or ( − 2)2 + ( + 6)2 + ( − 4)2 = 25. The intersection of this sphere with the -plane is the set of points on the sphere whose -coordinate is 0. Putting = 0 into the equation, we have ( − 2)2 + ( + 6)2 = 9 = 0 which represents a circle in the -plane with center (2 −60) and radius 3. To find the intersection with the -plane, we set = 0: ( − 2)2 + ( − 4)2 = −11. Since no points satisfy this equation, the sphere does not intersect the -plane. (Also note that the distance from the center of the sphere to the -plane is greater than the radius of the sphere.) To find the intersection with the -plane, we set = 0: ( + 6)2 + ( − 4)2 = 21 = 0, a circle in the -plane with center (0 −64) and radius √21. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.4 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 15. The radius of the sphere is the distance between (43 −1) and (3 8 1): = (3 − 4)2 + (8 − 3)2 + [1 − (−1)]2 = √30. Thus, an equation of the sphere is ( − 3)2 + ( − 8)2 + ( − 1)2 = 30. 16. If the sphere passes through the origin, the radius of the sphere must be the distance from the origin to the point (1 2 3): = (1 − 0)2 + (2 − 0)2 + (3 − 0)2 = √14. Then an equation of the sphere is ( − 1)2 + ( − 2)2 + ( − 3)2 = 14. 17. Completing squares in the equation 2 + 2 + 2 − 2 − 4 + 8 = 15 gives (2 − 2 + 1) + (2 − 4 + 4) + (2 + 8 + 16) = 15 + 1 + 4 + 16 ⇒ ( − 1)2 + ( − 2)2 + ( + 4)2 = 36, which we recognize as an equation of a sphere with center (12 −4) and radius 6. 18. Completing squares in the equation gives (2 + 8 + 16) + (2 − 6 + 9) + (2 + 2 + 1) = −17 + 16 + 9 + 1 ⇒ ( + 4)2 + ( − 3)2 + ( + 1)2 = 9, which we recognize as an equation of a sphere with center (−4 3 −1) and radius 3. 19. Completing squares in the equation 22 − 8 + 22 + 22 + 24 = 1 gives 2(2 − 4 + 4) + 22 + 2(2 + 12 + 36) = 1 + 8 + 72 ⇒ 2( − 2)2 + 22 + 2( + 6)2 = 81 ⇒ ( − 2)2 + 2 + ( + 6)2 = 81 2 , which we recognize as an equation of a sphere with center (20 −6) and radius 81 2 = 9√2. 20. Completing squares in the equation 32 + 32 − 6 + 32 − 12 = 10 gives 32 + 3(2 − 2 + 1) + 3(2 − 4 + 4) = 10 + 3 + 12 ⇒ 32 + 3( − 1)2 + 3( − 2)2 = 25 ⇒ 2 + ( − 1)2 + ( − 2)2 = 25 3 , which we recognize as an equation of a sphere with center (0 1 2) and radius 25 3 = 5√3. 21. (a) If the midpoint of the line segment from 1(1 1 1) to 2(2 2 2) is = 1 +2 2 1 +2 2 1 +2 2 , then the distances |1| and |2| are equal, and each is half of |12|. We verify that this is the case: |12| = (2 − 1)2 + (2 − 1)2 + (2 − 1)2 |1| = 1 2(1 + 2) − 12 + 1 2(1 + 2) − 12 + 1 2(1 + 2) − 12 = 1 22 − 1 212 + 1 22 − 1 212 + 1 22 − 1 212 = 1 22(2 − 1)2 + (2 − 1)2 + (2 − 1)2 = 1 2(2 − 1)2 + (2 − 1)2 + (2 − 1)2 = 1 2 |12| |2| = 2 − 1 2(1 + 2)2 + 2 − 1 2(1 + 2)2 + 2 − 1 2(1 + 2)2 = 1 22 − 1 212 + 1 22 − 1 212 + 1 22 − 1 212 = 1 22(2 − 1)2 + (2 − 1)2 + (2 − 1)2 = 1 2 (2 − 1)2 + (2 − 1)2 + (2 − 1)2 = 1 2 |12| So is indeed the midpoint of 12. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.1 THREE-DIMENSIONAL COORDINATE SYSTEMS ¤ 5 (b) By part (a), the midpoints of sides , and are 1− 1 214, 21 1 25 and 3 5 2 3 2 4. Then the lengths of the medians are: |2| = 02 + 1 2 − 22 + (5 − 3)2 = 9 4 + 4 = 25 4 = 5 2 |3| = 5 2 + 22 + 3 2 2 + (4 − 5)2 = 81 4 + 9 4 + 1 = 94 4 = 1 2√94 |1| = − 1 2 − 42 + (1 − 1)2 + (4 − 5)2 = 81 4 + 1 = 1 2√85 22. By Exercise 21(a), the midpoint of the diameter (and thus the center of the sphere) is 5+1 2 4+6 2 3+(2−9) = (35 −3). The radius is half the diameter, so = 1 2 (1 − 5)2 + (6 − 4)2 + (−9 − 3)2 = 1 2√164 = √41. Therefore an equation of the sphere is ( − 3)2 + ( − 5)2 + ( + 3)2 = 41. 23. (a) Since the sphere touches the -plane, its radius is the distance from its center, (2 −36), to the -plane, namely 6. Therefore = 6 and an equation of the sphere is ( − 2)2 + ( + 3)2 + ( − 6)2 = 62 = 36. (b) The radius of this sphere is the distance from its center (2 −36) to the -plane, which is 2. Therefore, an equation is ( − 2)2 + ( + 3)2 + ( − 6)2 = 4. (c) Here the radius is the distance from the center (2 −36) to the -plane, which is 3. Therefore, an equation is ( − 2)2 + ( + 3)2 + ( − 6)2 = 9. 24. The largest sphere contained in the first octant must have a radius equal to the minimum distance from the center (549) to any of the three coordinate planes. The shortest such distance is to the -plane, a distance of 4. Thus an equation of the sphere is ( − 5)2 + ( − 4)2 + ( − 9)2 = 16. 25. The equation = 5 represents a plane parallel to the -plane and 5 units in front of it. 26. The equation = −2 represents a plane parallel to the -plane and 2 units to the left of it. 27. The inequality 8 represents a half-space consisting of all points to the left of the plane = 8. 28. The inequality ≥ −1 represents a half-space consisting of all points on or above the plane = −1. 29. The inequality 0 ≤ ≤ 6 represents all points on or between the horizontal planes = 0 (the -plane) and = 6. 30. The equation 2 = 4 ⇔ = ±2 represents two vertical planes; = 2 is parallel to the -plane, two units to the right of it, and = −2 is two units to the left of it. 31. Because = −1, all points in the region must lie in the horizontal plane = −1. In addition, 2 + 2 = 4, so the region consists of all points that lie on a circle with radius 2 and center on the -axis that is contained in the plane = −1. 32. Here 2 + 2 = 4 with no restrictions on , so a point in the region must lie on a circle of radius 2, center on the -axis, but it could be in any horizontal plane = (parallel to the -plane). Thus the region consists of all possible circles 2 + 2 = 4, = and is therefore a circular cylinder with radius 2 whose axis is the -axis. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.6 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 33. The equation 2 + 2 + 2 = 4 is equivalent to 2 + 2 + 2 = 2, so the region consists of those points whose distance from the origin is 2. This is the set of all points on a sphere with radius 2 and center (0 0 0). 34. The inequality 2 + 2 + 2 ≤ 4 is equivalent to 2 + 2 + 2 ≤ 2, so the region consists of those points whose distance from the origin is at most 2. This is the set of all points on or inside a sphere with radius 2 and center (000). 35. The inequalities 1 ≤ 2 + 2 + 2 ≤ 5 are equivalent to 1 ≤ 2 + 2 + 2 ≤ √5, so the region consists of those points whose distance from the origin is at least 1 and at most √5. This is the set of all points on or between spheres with radii 1 and √5 and centers (0 00). 36. The equation = represents a plane perpendicular to the -plane and intersecting the -plane in the line = , = 0. 37. Here 2 + 2 ≤ 9 or equivalently √2 + 2 ≤ 3 which describes the set of all points in R3 whose distance from the -axis is at most 3. Thus the inequality represents the region consisting of all points on or inside a circular cylinder of radius 3 with axis the -axis. 38. The inequality 2 + 2 + 2 2 ⇔ 2 + 2 + ( − 1)2 1 is equivalent to 2 + 2 + ( − 1)2 1, so the region consists of those points whose distance from the point (001) is greater than 1. This is the set of all points outside the sphere with radius 1 and center (001). 39. This describes all points whose -coordinate is between 0 and 5, that is, 0 5. 40. For any point on or above the disk in the -plane with center the origin and radius 2 we have 2 + 2 ≤ 4. Also each point lies on or between the planes = 0 and = 8, so the region is described by 2 + 2 ≤ 4, 0 ≤ ≤ 8. 41. This describes a region all of whose points have a distance to the origin which is greater than , but smaller than . So inequalities describing the region are 2 + 2 + 2 , or 2 2 + 2 + 2 2. 42. The solid sphere itself is represented by 2 + 2 + 2 ≤ 2. Since we want only the upper hemisphere, we restrict the -coordinate to nonnegative values. Then inequalities describing the region are 2 + 2 + 2 ≤ 2, ≥ 0, or 2 + 2 + 2 ≤ 4, ≥ 0. 43. (a) To find the - and -coordinates of the point , we project it onto 2 and project the resulting point onto the - and -axes. To find the -coordinate, we project onto either the -plane or the -plane (using our knowledge of its - or -coordinate) and then project the resulting point onto the -axis. (Or, we could draw a line parallel to from to the -axis.) The coordinates of are (214). (b) is the intersection of 1 and 2, is directly below the -intercept of 2, and is directly above the -intercept of 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.1 THREE-DIMENSIONAL COORDINATE SYSTEMS ¤ 7 44. Let = ( ). Then 2| | = | | ⇔ 4| |2 = | |2 ⇔ 4( − 6)2 + ( − 2)2 + ( + 2)2 = ( + 1)2 + ( − 5)2 + ( − 3)2 ⇔ 42 − 12 + 36 − 2 − 2 + 42 − 4 + 4 − 2 + 10 + 42 + 4 + 4 − 2 + 6 = 35 ⇔ 32 − 50 + 32 − 6 + 32 + 22 = 35 − 144 − 16 − 16 ⇔ 2 − 50 3 + 2 − 2 + 2 + 22 3 = − 141 3 . By completing the square three times we get − 25 3 2 + ( − 1)2 + + 11 3 2 = 332 9 , which is an equation of a sphere with center 25 3 1 − 11 3 and radius √332 3 . 45. We need to find a set of points ( ) | | = | |. ( + 1)2 + ( − 5)2 + ( − 3)2 = ( − 6)2 + ( − 2)2 + ( + 2)2 ⇒ ( + 1)2 + ( − 5) + ( − 3)2 = ( − 6)2 + ( − 2)2 + ( + 2)2 ⇒ 2 + 2 + 1 + 2 − 10 + 25 + 2 − 6 + 9 = 2 − 12 + 36 + 2 − 4 + 4 + 2 + 4 + 4 ⇒ 14 − 6 − 10 = 9. Thus the set of points is a plane perpendicular to the line segment joining and (since this plane must contain the perpendicular bisector of the line segment ). 46. Completing the square three times in the first equation gives ( + 2)2 + ( − 1)2 + ( + 2)2 = 22, a sphere with center (−212) and radius 2. The second equation is that of a sphere with center (000) and radius 2. The distance between the centers of the spheres is (−2 − 0)2 + (1 − 0)2 + (−2 − 0)2 = √4 + 1 + 4 = 3. Since the spheres have the same radius, the volume inside both spheres is symmetrical about the plane containing the circle of intersection of the spheres. The distance from this plane to the center of the circles is 3 2. So the region inside both spheres consists of two caps of spheres of height = 2 − 3 2 = 1 2. From Exercise 5.2.49 [ET 6.2.49], the volume of a cap of a sphere is = 2 − 1 3 = 1 2 22 − 1 3 · 1 2 = 11 24 . So the total volume is 2 · 11 24 = 11 12 . 47. The sphere 2 + 2 + 2 = 4 has center (000) and radius 2. Completing squares in 2 − 4 + 2 − 4 + 2 − 4 = −11 gives (2 − 4 + 4) + (2 − 4 + 4) + (2 − 4 + 4) = −11 + 4 + 4 + 4 ⇒ ( − 2)2 + ( − 2)2 + ( − 2)2 = 1, so this is the sphere with center (222) and radius 1. The (shortest) distance between the spheres is measured along the line segment connecting their centers. The distance between (000) and (2 2 2) is (2 − 0)2 + (2 − 0)2 + (2 − 0)2 = √12 = 2√3, and subtracting the radius of each circle, the distance between the spheres is 2√3 − 2 − 1 = 2√3 − 3. 48. There are many different solids that fit the given description. However, any possible solid must have a circular horizontal cross-section at its top or at its base. Here we illustrate a solid with a circular base in the -plane. (A circular cross-section at the top results in an inverted version of the solid described below.) The vertical cross-section through the center of the base that is parallel to the -plane must be a square, and the vertical cross-section parallel to the -plane (perpendicular to the square) through the center of the base must be a triangle with two vertices on the circle and the third vertex at the center of the top side of the square. (See the figure.) [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.8 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE The solid can include any additional points that do not extend beyond these three "silhouettes" when viewed from directions parallel to the coordinate axes. One possibility shown here is to draw the circular base and the vertical square first. Then draw a surface formed by line segments parallel to the -plane that connect the top of the square to the circle. Problem 8 in the Problems Plus section at the end of the chapter illustrates another possible solid. 12.2 Vectors 1. (a) The cost of a theater ticket is a scalar, because it has only magnitude. (b) The current in a river is a vector, because it has both magnitude (the speed of the current) and direction at any given location. (c) If we assume that the initial path is linear, the initial flight path from Houston to Dallas is a vector, because it has both magnitude (distance) and direction. (d) The population of the world is a scalar, because it has only magnitude. 2. If the initial point of the vector h47i is placed at the origin, then h47i is the position vector of the point (4 7). 3. Vectors are equal when they share the same length and direction (but not necessarily location). Using the symmetry of the parallelogram as a guide, we see that −→ = −−→ , −−→ = −−→ , −−→ = −−→ , and −→ = −−→ . 4. (a) The initial point of −−→ is positioned at the terminal point of −→ , so by the Triangle Law the sum −→ + −−→ is the vector with initial point and terminal point , namely −→ . (b) By the Triangle Law, −−→ + −−→ is the vector with initial point and terminal point , namely −−→ . (c) First we consider −−→ − −→ as −−→ + −−→ . Then since −−→ has the same length as −→ but points in the opposite direction, we have − −→ = −→ and so −−→ − −→ = −−→ + −→ = −−→ . (d) We use the Triangle Law twice: −−→ + −→ + −→ = −−→ + −→ + −→ = −−→ + −→ = −−→ . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.2 VECTORS ¤ 9 5. (a) (b) (c) (d) (e) (f) 6. (a) (b) (c) (d) (e) (f) 7. Because the tail of d is the midpoint of we have −→ = 2d, and by the Triangle Law, a + 2d = b ⇒ 2d = b − a ⇒ d = 1 2(b − a) = 1 2b − 1 2a. Again by the Triangle Law we have c + d = b so c = b − d = b − 1 2b − 1 2a = 1 2a + 1 2b. 8. We are given u + v + w = 0, so w = (−u) + (−v). (See the figure.) Vectors −u, −v, and w form a right triangle, so from the Pythagorean Theorem we have |−u|2 + |−v|2 = |w|2. But |−u| = |u| = 1 and |−v| = |v| = 1 so |w| = |−u|2 + |−v|2 = √2. 9. a = h1 − (−2)2 − 1i = h3 1i 10. a = h−3 − (−5) 3 − (−1)i = h24i 11. a = h2 − 33 − (−1)i = h−14i 12. a = h1 − 30 − 2i = h−2 −2i °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.10 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 13. a = h2 − 03 − 3 −1 − 1i = h20 −2i 14. a = h3 − 04 − 6 4 − (−1)i = h3 −25i 15. h−14i + h6 −2i = h−1 + 64 + (−2)i = h52i 16. h3 −1i + h−15i = h3 + (−1) −1 + 5i = h24i 17. h30 1i + h0 8 0i = h3 + 00 + 81 + 0i = h381i 18. h1 3 −2i + h006i = h1 + 03 + 0 −2 + 6i = h1 34i 19. a + b = h−34i + h9 −1i = h−3 + 9 4 + (−1)i = h63i 4a + 2b = 4h−34i + 2h9 −1i = h−1216i + h18 −2i = h6 14i |a| = (−3)2 + 42 = √25 = 5 |a − b| = |h−3 − 9 4 − (−1)i| = |h−12 5i| = (−12)2 + 52 = √169 = 13 20. a + b = (5i + 3j) + (−i − 2j) = 4i + j 4a + 2b = 4(5i + 3j) + 2(−i − 2j) = 20i + 12j − 2i − 4j = 18i + 8j |a| = √52 + 32 = √34 |a − b| = |(5i + 3j) − (−i − 2j)| = |6i + 5j| = √62 + 52 = √61 21. a + b = (4i − 3j + 2k) + (2i − 4k) = 6i − 3j − 2k 4a + 2b = 4(4i − 3j + 2k) + 2(2i − 4k) = 16i − 12j + 8k + 4i − 8k = 20i − 12j |a| = 42 + (−3)2 + 22 = √29 |a − b| = |(4i − 3j + 2k) − (2i − 4k)| = |2i − 3j + 6k| = 22 + (−3)2 + 62 = √49 = 7 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.2 VECTORS ¤ 11 22. a + b = h8 + 51 + (−2) −4 + 1i = h13 −1 −3i 4a + 2b = 4h8 1 −4i + 2h5 −21i = h324 −16i + h10 −4 2i = h42 0 −14i |a| = 82 + 12 + (−4)2 = √81 = 9 |a − b| = |h8 − 51 − (−2) −4 − 1i| = |h33 −5i| = 32 + 32 + (−5)2 = √43 23. The vector h6 −2i has length |h6 −2i| = 62 + (−2)2 = √40 = 2√10, so by Equation 4 the unit vector with the same direction is 1 2√10 h6 −2i = √310 −√110. 24. The vector −5i + 3j − k has length |−5i + 3j − k| = (−5)2 + 32 + (−1)2 = √35, so by Equation 4 the unit vector with the same direction is √135(−5i + 3j − k) = −√535 i + √335 j − √135 k. 25. The vector 8i − j + 4k has length |8i − j + 4k| = 82 + (−1)2 + 42 = √81 = 9, so by Equation 4 the unit vector with the same direction is 1 9(8i − j + 4k) = 8 9 i − 1 9 j + 4 9 k. 26. |h6 2 −3i| = 62 + 22 + (−3)2 = √49 = 7, so a unit vector in the direction of h62 −3i is u = 1 7 h62 −3i. A vector in the same direction but with length 4 is 4u = 4 · 1 7 h6 2 −3i = 24 7 8 7 − 12 7 . 27. From the figure, we see that tan = √3 1 = √3 ⇒ = 60◦. 28. From the figure we see that tan = 6 8 = 3 4, so = tan−1 3 4 ≈ 369◦. 29. From the figure, we see that the -component of v is 1 = |v|cos(3) = 4 · 1 2 = 2 and the -component is 2 = |v|sin(3) = 4 · √23 = 2√3 Thus v = h1 2i = 22√3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.12 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 30. From the figure, we see that the horizontal component of the force F is |F|cos38◦ = 50 cos 38◦ ≈ 394 N, and the vertical component is |F|sin 38◦ = 50 sin 38◦ ≈ 308 N. 31. The velocity vector v makes an angle of 40◦ with the horizontal and has magnitude equal to the speed at which the football was thrown. From the figure, we see that the horizontal component of v is |v|cos 40◦ = 60 cos 40◦ ≈ 4596 ft/s and the vertical component is |v|sin 40◦ = 60 sin 40◦ ≈ 3857 ft/s. 32. The given force vectors can be expressed in terms of their horizontal and vertical components as 20 cos 45◦ i + 20 sin 45◦ j = 10√2i + 10√2j and 16 cos 30◦ i − 16 sin 30◦ j = 8√3i − 8j. The resultant force F is the sum of these two vectors: F = 10√2 + 8√3i + 10√2 − 8j ≈ 2800i + 614j. Then we have |F| ≈ (2800)2 + (614)2 ≈ 287 lb and, letting be the angle F makes with the positive -axis, tan = 10√2 − 8 10√2 + 8√3 ⇒ = tan−11010 √√2 + 8 2 −√8 3 ≈ 124◦. 33. The given force vectors can be expressed in terms of their horizontal and vertical components as −300i and 200cos60◦ i + 200sin60◦ j = 200 1 2 i + 200 √23 j = 100i + 100√3j. The resultant force F is the sum of these two vectors: F = (−300 + 100)i + 0 + 100√3j = −200i + 100√3j. Then we have |F| ≈ (−200)2 + 100√32 = √70,000 = 100√7 ≈ 2646 N. Let be the angle F makes with the positive -axis. Then tan = 100√3 −200 = − √3 2 and the terminal point of F lies in the second quadrant, so = tan−1−√23 + 180◦ ≈ −409◦ + 180◦ = 1391◦. 34. Set up the coordinate axes so that north is the positive -direction, and east is the positive -direction. The wind is blowing at 50 kmh from the direction N45◦W, so that its velocity vector is 50 kmh S45◦E, which can be written as vwind = 50(cos45◦i − sin45◦j). With respect to the still air, the velocity vector of the plane is 250 kmh N60◦E, or equivalently vplane = 250(cos30◦i + sin30◦j). The velocity of the plane relative to the ground is v = vplane + vwind = (250cos30◦ + 50cos45◦)i + (250sin30◦ − 50sin45◦)j = 125√3 + 25√2i + 125 − 25√2j ≈ 2519i + 896j (See the figure.) The ground speed is |v| ≈ (2519)2 + (896)2 ≈ 267 kmh. The angle the velocity vector makes with the -axis is ≈ tan−1 251 8969 ≈ 20◦. Therefore, the true course of the plane is about N(90 − 20)◦E = N 70◦E. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.2 VECTORS ¤ 13 35. With respect to the water’s surface, the woman’s velocity is the vector sum of the velocity of the ship with respect to the water, and the woman’s velocity with respect to the ship. If we let north be the positive -direction, then v = h022i + h−30i = h−322i. The woman’s speed is |v| = √9 + 484 ≈ 222 mih. The vector v makes an angle with the east, where = tan−1 −223 ≈ 98◦. Therefore, the woman’s direction is about N(98 − 90)◦W = N8◦W. 36. Let T1 and T2 be the tension vectors corresponding to the support cables as shown in the figure. In terms of vertical and horizontal components, T1 = |T1|cos 60◦i + |T1|sin 60◦j = 1 2 |T1| i + √3 2 |T1| j T2 = − |T2|cos 60◦i + |T2|sin 60◦j = −1 2 |T2| i + √3 2 |T2| j The resultant of these tensions, T1 + T2, counterbalances the weight w = −500j. So T1 + T2 = −w = 500j ⇒ 21 |T1| i + √23 |T1| j + −1 2 |T2| i + √23 |T2| j = 500j. Equating -components gives 1 2 |T1| i − 1 2 |T2| i = 0, so |T1| = |T2| (as we would expect from the symmetry of the problem). Equating -components, we have √3 2 |T1| j + √3 2 |T2| j = √3|T1| j = 500j ⇒ |T1| = 500 √3 . Thus the magnitude of each tension is |T1| = |T2| = 500 √3 ≈ 28868 lb. The tension vectors are T1 = 1 2 |T1| i + √3 2 |T1| j = 250 √3 i + 250j ≈ 14434i + 250j and T2 = −250 √3 i + 250j ≈ −14434i + 250j. 37. Call the two tension vectors T2 and T3, corresponding to the ropes of length 2 m and 3 m. In terms of vertical and horizontal components, T2 = − |T2|cos 50◦i + |T2|sin 50◦j (1) and T3 = |T3|cos 38◦i + |T3| sin 38◦j (2) The resultant of these forces, T2 + T3, counterbalances the weight of the hoist (which is −350j), so T2 + T3 = 350j ⇒ (− |T2|cos 50◦ + |T3| cos 38◦)i + (|T2|sin 50◦ + |T3|sin 38◦)j = 350j. Equating components, we have − |T2|cos 50◦ + |T3|cos 38◦ = 0 ⇒ |T2| = |T3| cos 38◦ cos 50◦ and |T2|sin 50◦ + |T3| sin 38◦ = 350. Substituting the first equation into the second gives |T3| cos 38◦ cos 50◦ sin 50◦ + |T3|sin 38◦ = 350 ⇒ |T3|(cos 38◦ tan 50◦ + sin 38◦) = 350, so the magnitudes of the tensions are |T3| = 350 cos 38◦ tan 50◦ + sin 38◦ ≈ 22511 N and |T2| = |T3| cos 38◦ cos 50◦ ≈ 27597 N. Finally, from (1) and (2), the tension vectors are T2 ≈ −17739i + 21141j and T3 ≈ 17739i + 13859j. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.14 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 38. We can consider the weight of the chain to be concentrated at its midpoint. The forces acting on the chain then are the tension vectors T1, T2 in each end of the chain and the weight w, as shown in the figure. We know |T1| = |T2| = 25 N so, in terms of vertical and horizontal components, we have T1 = −25 cos 37◦i + 25 sin 37◦j T2 = 25 cos 37◦i + 25 sin 37◦j The resultant vector T1 + T2 of the tensions counterbalances the weight w giving T1 + T2 = −w Since w = − |w|j, we have (−25 cos 37◦i + 25 sin 37◦j) + (25 cos 37◦i + 25 sin 37◦j) = |w|j ⇒ 50 sin 37◦j = |w|j ⇒ |w| = 50 sin 37◦ ≈ 301. So the weight is 301 N, and since = , the mass is 30 981 ≈ 307 kg. 39. (a) Set up coordinate axes so that the boatman is at the origin, the canal is bordered by the -axis and the line = 3, and the current flows in the negative -direction. The boatman wants to reach the point (32). Let be the angle, measured from the positive -axis, in the direction he should steer. (See the figure.) In still water, the boat has velocity v = h13 sin13 cos i and the velocity of the current is v h0 −35i, so the true path of the boat is determined by the velocity vector v = v + v = h13 sin13 cos − 35i. Let be the time (in hours) after the boat departs; then the position of the boat at time is given by v and the boat crosses the canal when v = h13 sin13 cos − 35i = h3 2i. Thus 13(sin) = 3 ⇒ = 3 13 sin and (13 cos − 35) = 2. Substituting gives (13 cos − 35) 3 13 sin = 2 ⇒ 39 cos − 105 = 26 sin (1). Squaring both sides, we have 1521 cos2 − 819 cos + 11025 = 676 sin2 = 6761 − cos2 2197 cos2 − 819 cos − 56575 = 0 The quadratic formula gives cos = 819 ± (−819)2 − 4(2197)(−56575) 2(2197) = 819 ± √5,642,572 4394 ≈ 072699 or − 035421 The acute value for is approximately cos−1(072699) ≈ 434◦. Thus the boatman should steer in the direction that is 434◦ from the bank, toward upstream. Alternate solution: We could solve (1) graphically by plotting = 39cos − 105 and = 26sin on a graphing device and finding the appoximate intersection point (07571785). Thus ≈ 0757 radians or equivalently 434◦. (b) From part (a) we know the trip is completed when = 3 13sin . But ≈ 434◦, so the time required is approximately 3 13sin434◦ ≈ 0336 hours or 202 minutes. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.2 VECTORS ¤ 15 40. Let v1, v2, and v3 be the force vectors where |v1| = 25, |v2| = 12, and |v3| = 4. Set up coordinate axes so that the object is at the origin and v1, v2 lie in the -plane. We can position the vectors so that v1 = 25i, v2 = 12 cos 100◦ i + 12 sin 100◦ j, and v3 = 4k. The magnitude of a force that counterbalances the three given forces must match the magnitude of the resultant force. We have v1 + v2 + v3 = (25 + 12 cos 100◦)i + 12 sin 100◦ j + 4k, so the counterbalancing force must have magnitude |v1 + v2 + v3| = (25 + 12 cos 100◦)2 + (12 sin 100◦)2 + 42 ≈ 261 N. 41. The slope of the tangent line to the graph of = 2 at the point (24) is =2 = 2 =2 = 4 and a parallel vector is i + 4j which has length |i + 4j| = √12 + 42 = √17, so unit vectors parallel to the tangent line are ± √117 (i + 4j). 42. (a) The slope of the tangent line to the graph of = 2 sin at the point (61) is =6 = 2 cos =6 = 2 · √3 2 = √3 and a parallel vector is i + √3j which has length i + √3j = 12 + √32 = √4 = 2, so unit vectors parallel to the tangent line are ± 1 2i + √3j. (b) The slope of the tangent line is √3, so the slope of a line perpendicular to the tangent line is − √13 and a vector in this direction is √3i− j. Since √3i − j = √32 + (−1)2 = 2, unit vectors perpendicular to the tangent line are ± 1 2√3i − j. (c) 43. By the Triangle Law, −→ + −−→ = −→ . Then −→ + −−→ + −→ = −→ + −→ , but −→ + −→ = −→ + −−→ = 0. So −→ + −−→ + −→ = 0. 44. −→ = 1 3 −→ and −−→ = 2 3 −→ . c = −→ + −→ = a + 1 3 −→ ⇒ −→ = 3c − 3a. c = −−→ + −−→ = −→ + 2 3 −→ ⇒ −→ = 3 2 c − 3 2 b. −→ = −−→ , so 3 2 c − 3 2 b = 3a − 3c ⇔ c + 2c = 2a + b ⇔ c = 2 3 a + 1 3 b. 45. (a), (b) (c) From the sketch, we estimate that ≈ 13 and ≈ 16. (d) c = a + b ⇔ 7 = 3 + 2 and 1 = 2 − . Solving these equations gives = 9 7 and = 11 7 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.16 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 46. Draw a, b, and c emanating from the origin. Extend a and b to form lines and , and draw lines 0 and 0 parallel to these two lines through the terminal point of c. Since a and b are not parallel, and 0 must meet (at ), and 0 and must also meet (at ). Now we see that −−→ + −−→ = c, so if = −−→ |a| or its negative, if a points in the direction opposite −−→ and = −−→ |b| (or its negative, as in the diagram), then c = a + b, as required. Argument using components: Since a, b, and c all lie in the same plane, we can consider them to be vectors in two dimensions. Let a = h1 2i, b = h1 2i, and c = h1 2i. We need 1 + 1 = 1 and 2 + 2 = 2. Multiplying the first equation by 2 and the second by 1 and subtracting, we get = 21 − 12 21 − 12 . Similarly = 221 1 − − 1 1 22 . Since a 6= 0 and b 6= 0 and a is not a scalar multiple of b, the denominator is not zero. 47. |r − r0| is the distance between the points ( ) and (0 0 0), so the set of points is a sphere with radius 1 and center (0 0 0). Alternate method: |r − r0| = 1 ⇔ ( − 0)2 + ( − 0)2 + ( − 0)2 = 1 ⇔ ( − 0)2 + ( − 0)2 + ( − 0)2 = 1, which is the equation of a sphere with radius 1 and center (0 0 0). 48. Let 1 and 2 be the points with position vectors r1 and r2 respectively. Then |r − r1| + |r − r2| is the sum of the distances from ( ) to 1 and 2. Since this sum is constant, the set of points ( ) represents an ellipse with foci 1 and 2. The condition |r1 − r2| assures us that the ellipse is not degenerate. 49. a + (b + c) = h1 2i + (h1 2i + h1 2i) = h1 2i + h1 + 1 2 + 2i = h1 + 1 + 1 2 + 2 + 2i = h(1 + 1) + 1 (2 + 2) + 2i = h1 + 1 2 + 2i + h1 2i = (h1 2i + h1 2i) + h1 2i = (a + b) + c 50. Algebraically: (a + b) = (h1 2 3i + h1 2 3i) = h1 + 1 2 + 2 3 + 3i = h(1 + 1) (2 + 2) (3 + 3)i = h1 + 1 2 + 2 3 + 3i = h1 2 3i + h1 2 3i = a + b Geometrically: According to the Triangle Law, if a = −−→ and b = −→ , then a + b = −→ . Construct triangle as shown so that −→ = a and −→ = b. (We have drawn the case where 1.) By the Triangle Law, −→ = a + b. But triangle and triangle are similar triangles because b is parallel to b. Therefore, −→ and −→ are parallel and, in fact, −→ = −→ . Thus, a + b = (a + b). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.3 THE DOT PRODUCT ¤ 17 51. Consider triangle , where and are the midpoints of and . We know that −→ + −−→ = −→ (1) and −−→ + −−→ = −−→ (2). However, −−→ = 1 2 −→ , and −−→ = 1 2 −−→ . Substituting these expressions for −−→ and −−→ into (2) gives 1 2 −→ + 1 2 −−→ = −−→ . Comparing this with (1) gives −−→ = 1 2 −→ . Therefore −→ and −−→ are parallel and −−→ = 1 2 −→ . 52. The question states that the light ray strikes all three mirrors, so it is not parallel to any of them and 1 6= 0, 2 6= 0 and 3 6= 0. Let b = h1 2 3i, as in the diagram. We can let |b| = |a|, since only its direction is important. Then |2| |b| = sin = ||a2|| ⇒ |2| = |2|. From the diagram 2 j and 2 j point in opposite directions, so 2 = −2. || = ||, so |3| = sin || = sin || = |3|, and |1| = cos || = cos || = |1|. 3 k and 3 k have the same direction, as do 1 i and 1 i, so b = h1 −2 3i. When the ray hits the other mirrors, similar arguments show that these reflections will reverse the signs of the other two coordinates, so the final reflected ray will be h−1 −2 −3i = −a, which is parallel to a. 12.3 The Dot Product 1. (a) a · b is a scalar, and the dot product is defined only for vectors, so (a · b) · c has no meaning. (b) (a · b)c is a scalar multiple of a vector, so it does have meaning. (c) Both |a| and b · c are scalars, so |a|(b · c) is an ordinary product of real numbers, and has meaning. (d) Both a and b + c are vectors, so the dot product a · (b + c) has meaning. (e) a · b is a scalar, but c is a vector, and so the two quantities cannot be added and a · b + c has no meaning. (f ) |a| is a scalar, and the dot product is defined only for vectors, so |a| · (b + c) has no meaning. 2. a · b = h5 −2i · h34i = (5)(3) + (−2)(4) = 15 − 8 = 7 3. a · b = h1504i · h−46i = (15)(−4) + (04)(6) = −6 + 24 = −36 4. a · b = h6 −23i · h2 5 −1i = (6)(2) + (−2)(5) + (3)(−1) = 12 − 10 − 3 = −1 5. a · b = 4 1 1 4 · h6 −3 −8i = (4)(6) + (1)(−3) + 1 4(−8) = 19 6. a · b = h −2i · h2 −i = ()(2) + (−)() + (2)(−) = 2 − − 2 = − °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.18 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 7. a · b = (2i + j) · (i − j + k) = (2)(1) + (1)(−1) + (0)(1) = 1 8. a · b = (3i + 2j − k) · (4i + 5k) = (3)(4) + (2)(0) + (−1)(5) = 7 9. By Theorem 3, a · b = |a| |b|cos = (7)(4 ) cos 30 ◦ = 28 √23 = 14√3 ≈ 2425. 10. By Theorem 3, a · b = |a| |b|cos = (80)(50)cos 34 = 4000− √22 = −2000√2 ≈ −282843. 11. u v and w are all unit vectors, so the triangle is an equilateral triangle. Thus the angle between u and v is 60◦ and u · v = |u| |v|cos 60◦ = (1)(1) 1 2 = 1 2 If w is moved so it has the same initial point as u, we can see that the angle between them is 120◦ and we have u · w = |u| |w| cos 120◦ = (1)(1)− 1 2 = − 1 2. 12. u is a unit vector, so w is also a unit vector, and |v| can be determined by examining the right triangle formed by u and v Since the angle between u and v is 45◦, we have |v| = |u|cos 45◦ = √22. Then u · v = |u| |v|cos 45◦ = (1) √22 √22 = 1 2. Since u and w are orthogonal, u · w = 0. 13. (a) i · j = h1 0 0i · h010i = (1)(0) + (0)(1) + (0)(0) = 0. Similarly, j · k = (0)(0) + (1)(0) + (0)(1) = 0 and k · i = (0)(1) + (0)(0) + (1)(0) = 0. Another method: Because i, j, and k are mutually perpendicular, the cosine factor in each dot product (see Theorem 3) is cos 2 = 0. (b) By Property 1 of the dot product, i · i = |i|2 = 12 = 1 since i is a unit vector. Similarly, j · j = |j|2 = 1 and k · k = |k|2 = 1. 14. The dot product A · P is h i · h4251i = (4) + (25) + (1) = (number of hamburgers sold)(price per hamburger) +(number of hot dogs sold)(price per hot dog) +(number of soft drinks sold)(price per soft drink) so it is equal to the vendor’s total revenue for that day. 15. |a| = √42 + 32 = 5, |b| = 22 + (−1)2 = √5, and a · b = (4)(2) + (3)(−1) = 5. From Corollary 6, we have cos = a · b |a| |b| = 5 5 · √5 = 1 √ 5 . So the angle between a and b is = cos−1√15 ≈ 63◦. 16. |a| = (−2)2 + 52 = √29, |b| = √52 + 122 = 13, and a · b = (−2)(5) + (5)(12) = 50. Using Corollary 6, we have cos = a · b |a| |b| = 50 √29 · 13 = 50 13√29 and the angle between a and b is = cos−11350 √29 ≈ 44◦. 17. |a| = 12 + (−4)2 + 12 = √18 = 3√2, |b| = 02 + 22 + (−2)2 = √8 = 2√2, and a · b = (1)(0) + (−4)(2) + (1)(−2) = −10. From Corollary 6, we have cos = a · b |a| |b| = −10 3√2 · 2√2 = − 10 12 = − 5 6 and the angle between a and b is = cos−1− 5 6 ≈ 146◦. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.3 THE DOT PRODUCT ¤ 19 18. |a| = (−1)2 + 32 + 42 = √26, |b| = √52 + 22 + 12 = √30, and a · b = (−1)(5) + (3)(2) + (4)(1) = 5. Then cos = a · b |a| |b| = 5 √26 · √30 = 5 √780 = 5 2√195 and = cos−12√5195 ≈ 80◦. 19. |a| = 42 + (−3)2 + 12 = √26, |b| = 22 + 02 + (−1)2 = √5, and a · b = (4)(2) + (−3)(0) + (1)(−1) = 7. Then cos = a · b |a| |b| = 7 √26 · √5 = 7 √130 and = cos−1√130 7 ≈ 52◦. 20. |a| = 82 + (−1)2 + 42 = √81 = 9, |b| = √02 + 42 + 22 = √20 = 2√5, and a · b = (8)(0) + (−1)(4) + (4)(2) = 4. Then cos = a · b |a| |b| = 4 9 · 2√5 = 2 9√5 and = cos−19√25 ≈ 84◦. 21. Let , , and be the angles at vertices , , and respectively. Then is the angle between vectors −−→ and −→ , is the angle between vectors −−→ and −→ , and is the angle between vectors −→ and −→ . Thus cos = −−→ · −→ −−→ −→ = h−23i · h14i (−2)2 + 32 √12 + 42 = −2 + 12 √13√17 = 10 √221 and = cos−1√10 221 ≈ 48◦. Similarly, cos = −−→ · −→ −−→ −→ = h2 −3i · h31i √4 + 9√9 + 1 = 6 − 3 √13√10 = 3 √130 so = cos−1√130 3 ≈ 75◦ and ≈ 180◦ − (48◦+ 75◦) = 57◦. Alternate solution: Apply the Law of Cosines three times as follows: cos = −→ 2 − −−→ 2 − −→ 2 2 −−→ −→ , cos = −→ 2 − −−→ 2 − −→ 2 2 −−→ −→ , and cos = −−→ 2 − −→ 2 − −→ 2 2 −→ −→ . 22. Let , , and be the angles at vertices , , and . Then is the angle between vectors −→ and −→ , is the angle between vectors −→ and −−→ , and is the angle between vectors −→ and −−→ . Thus cos = −→ · −→ −→ −→ = h2 −2 1i · h034i 22 + (−2)2 + 12 √02 + 32 + 42 = 0 − 6 + 4 3 · 5 = − 2 15 and = cos−1− 15 2 ≈ 98◦. Similarly, cos = −→ · −−→ −→ −−→ = h−22 −1i · h−2 5 3i √4 + 4 + 1√4 + 25 + 9 = 4 + 10 − 3 3 · √38 = 11 3√38 so = cos−13√1138 ≈ 54◦ and ≈ 180◦ − (98◦+ 54◦) = 28◦. [continued] °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.20 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE Alternate solution: Apply the Law of Cosines three times as follows: cos = −−→ 2 − −→ 2 − −→ 2 2 −→ −→ cos = −→ 2 − −→ 2 − −−→ 2 2 −→ −−→ cos = −→ 2 − −→ 2 − −−→ 2 2 −→ −−→ 23. (a) a · b = (9)(−2) + (3)(6) = 0, so a and b are orthogonal (and not parallel). (b) a · b = (4)(3) + (5)(−1) + (−2)(5) = −3 6= 0, so a and b are not orthogonal. Also, since a is not a scalar multiple of b, a and b are not parallel. (c) a · b = (−8)(6) + (12)(−9) + (4)(−3) = −168 6= 0, so a and b are not orthogonal. Because a = − 4 3 b, a and b are parallel. (d) a · b = (3)(5) + (−1)(9) + (3)(−2) = 0, so a and b are orthogonal (and not parallel). 24. (a) u · v = (−5)(3) + (4)(4) + (−2)(−1) = 3 6= 0, so u and v are not orthogonal. Also, u is not a scalar multiple of v, so u and v are not parallel. (b) u · v =(9)(−6) + (−6)(4) + (3)(−2) = −84 6= 0, so u and v are not orthogonal. Because u = − 3 2 v, u and v are parallel. (c) u · v =()() + ()(0) + ()(−) = 2 + 0 − 2 = 0, so u and v are orthogonal (and not parallel). (Note that if = 0 then u = v = 0, and the zero vector is considered orthogonal to all vectors. Although in this case u and v are identical, they are not considered parallel, as only nonzero vectors can be parallel.) 25. −−→ = h−1 −32i, −→ = h4 −2 −1i, and −−→ · −→ = −4 + 6 − 2 = 0. Thus −−→ and −→ are orthogonal, so the angle of the triangle at vertex is a right angle. 26. By Theorem 3, vectors h2 1 −1i and h1 0i meet at an angle of 45◦ when h21 −1i · h1 0i = √4 + 1 + 1√1 + 2 + 0 cos 45◦ or 2 + − 0 = √6√1 + 2 · √22 ⇔ 2 + = √3√1 + 2. Squaring both sides gives 4 + 4 + 2 = 3 + 32 ⇔ 22 − 4 − 1 = 0. By the quadratic formula, = −(−4) ± (−4)2 − 4(2)(−1) 2(2) = 4 ± √24 4 = 4 ± 2√6 4 = 1 ± √6 2 . (You can verify that both values are valid.) 27. Let a = 1 i + 2 j + 3 k be a vector orthogonal to both i + j and i + k. Then a · (i + j) = 0 ⇔ 1 + 2 = 0 and a · (i + k) = 0 ⇔ 1 + 3 = 0, so 1 = −2 = −3. Furthermore a is to be a unit vector, so 1 = 2 1 + 2 2 + 2 3 = 32 1 implies 1 = ± √13. Thus a = √13 i − √13 j − √13 k and a = − √13 i + √13 j + √13 k are two such unit vectors. 28. Let u = h i be a unit vector. By Theorem 3 we need u · v = |u| |v| cos 60◦ ⇔ 3 + 4 = (1)(5) 1 2 ⇔ = 5 8 − 3 4 . Since u is a unit vector, |u| = √2 + 2 = 1 ⇔ 2 + 2 = 1 ⇔ 2 + 5 8 − 3 42 = 1 ⇔ 25 162 − 15 16 + 25 64 = 1 ⇔ 1002 − 60 − 39 = 0 By the quadratic formula, = −(−60) ± (−60)2 − 4(100)(−39) 2(100) = 60 ± √19,200 200 = 3 ± 4√3 10 . If = 3 + 4√3 10 then °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.3 THE DOT PRODUCT ¤ 21 = 5 8 − 3 4 3 + 4 10√3 = 4 −10 3√3, and if = 3 −10 4√3 then = 5 8 − 343 −10 4√3 = 4 + 3 10√3. Thus the two unit vectors are 3 + 4 10√3 4 −10 3√3 ≈ h09928 −01196i and 3 −10 4√3 4 + 3 10√3 ≈ h−03928 09196i. 29. The line 2 − = 3 ⇔ = 2 − 3 has slope 2, so a vector parallel to the line is a = h1 2i. The line 3 + = 7 ⇔ = −3 + 7 has slope −3, so a vector parallel to the line is b = h1 −3i. The angle between the lines is the same as the angle between the vectors. Here we have a · b = (1)(1) + (2)(−3) = −5, |a| = √12 + 22 = √5, and |b| = 12 + (−3)2 = √10, so cos = a · b |a| |b| = −5 √5 · √10 = −5 5√2 = − 1 √ 2 or − √2 2 . Thus = 135◦, and the acute angle between the lines is 180◦ − 135◦ = 45◦. 30. The line + 2 = 7 ⇔ = − 1 2 + 7 2 has slope − 1 2 , so a vector parallel to the line is a = h2 −1i. The line 5 − = 2 ⇔ = 5 − 2 has slope 5, so a vector parallel to the line is b = h15i. The lines meet at the same angle that the vectors meet at. Here we have a · b = (2)(1) + (−1)(5) = −3, |a| = 22 + (−1)2 = √5, and |b| = √12 + 52 = √26, so cos = a · b |a| |b| = −3 √5 · √26 = −3 √130 and = cos−1 √−130 3 ≈ 1053◦. The acute angle between the lines is approximately 180◦ − 1053◦ = 747◦. 31. The curves = 2 and = 3 meet when 2 = 3 ⇔ 3 − 2 = 0 ⇔ 2( − 1) = 0 ⇔ = 0, = 1. We have 2 = 2 and 3 = 32, so the tangent lines of both curves have slope 0 at = 0. Thus the angle between the curves is 0◦ at the point (0 0). For = 1, 2 =1 = 2 and 3 =1 = 3 so the tangent lines at the point (11) have slopes 2 and 3. Vectors parallel to the tangent lines are h1 2i and h1 3i, and the angle between them is given by cos = h12i · h13i |h12i| |h13i| = 1 + 6 √5√10 = 7 5√2 Thus = cos−1 5√72 ≈ 81◦. 32. The curves = sin and = cos meet when sin = cos ⇔ tan = 1 ⇔ = 4 [0 ≤ ≤ 2]. Thus the point of intersection is 4 √22. We have sin =4 = cos =4 = √22 and cos =4 = −sin =4 = − √2 2 , so the tangent lines at that point have slopes √2 2 and − √2 2 . Vectors parallel to the tangent lines are 1 √22 and 1 −√22, and the angle between them is given by cos = 1 √22 · 1 −√22 1 √22 1 −√22 = 1 − 1 2 3 2 3 2 = 12 32 = 1 3 Thus = cos−1 1 3 ≈ 705◦. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.22 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 33. Since |h21 2i| = √4 + 1 + 4 = √9 = 3, using Equations 8 and 9 we have cos = 2 3, cos = 1 3, and cos = 2 3. The direction angles are given by = cos−1 2 3 ≈ 48◦, = cos−1 1 3 ≈ 71◦, and = cos−1 2 3 = 48◦. 34. Since |h63 −2i| = √36 + 9 + 4 = √49 = 7, using Equations 8 and 9 we have cos = 6 7, cos = 3 7, and cos = −72. The direction angles are given by = cos−1 6 7 ≈ 31◦, = cos−1 3 7 ≈ 65◦, and = cos−1− 2 7 = 107◦. 35. Since |i − 2j − 3k| = √1 + 4 + 9 = √14, Equations 8 and 9 give cos = √114, cos = √−14 2 , and cos = √−14 3 , while = cos−1 √114 ≈ 74◦, = cos−1− √214 ≈ 122◦, and = cos−1− √314 ≈ 143◦. 36. Since 1 2 i + j + k = 1 4 + 1 + 1 = 9 4 = 3 2, Equations 8 and 9 give cos = 1 3 2 2 = 1 3, cos = cos = 312 = 2 3, while = cos−1 1 3 ≈ 71◦ and = = cos−1 2 3 ≈ 48◦. 37. |h i| = √2 + 2 + 2 = √3 [since 0], so cos = cos = cos = √3 = √13 and = = = cos−1 √13 ≈ 55◦. 38. Since cos2 + cos2 + cos2 = 1, cos2 = 1 − cos2 − cos2 = 1 − cos2 4 − cos2 3 = 1 − √22 2 − 1 2 2 = 1 4. Thus cos = ± 1 2 and = 3 or = 23 . 39. |a| = (−5)2 + 122 = √169 = 13. The scalar projection of b onto a is compa b = a · b |a| = −5 · 4 + 12 · 6 13 = 4 and the vector projection of b onto a is proja b = a|a· |b |aa| = 4 · 13 1 h−512i = − 20 13 48 13 . 40. |a| = √12 + 42 = √17. The scalar projection of b onto a is compa b = a · b |a| = 1 · 2 + 4 · 3 √17 = 14 √17 and the vector projection of b onto a is proja b = a|a· |b |aa| = √14 17 · √117h14i = 14 17 56 17 . 41. |a| = 42 + 72 + (−4)2 = √81 = 9 so the scalar projection of b onto a is compab = a · b |a| = (4)(3) + (7)(−1) + (−4)(1) 9 = 1 9 . The vector projection of b onto a is projab = a|a· |b |aa| = 1 9 · 1 9 h47 −4i = 81 1 h4 7 −4i = 81 4 81 7 − 81 4 . 42. |a| = √1 + 16 + 64 = √81 = 9 so the scalar projection of b onto a is compa b = a · b |a| = 1 9 (−12 + 4 + 16) = 8 9, while the vector projection of b onto a is proja b = a|a· |b |aa| = 8 9 · 1 9 h−14 8i = 81 8 h−148i = − 81 8 32 81 64 81 . 43. |a| = √9 + 9 + 1 = √19 so the scalar projection of b onto a is compa b = a · b |a| = 6 − 12 − 1 √19 = − 7 √19 while the vector projection of b onto a is proja b = −√719 |a a| = − √719 · √119 (3i − 3j + k) = − 19 7 (3i− 3j+k) = − 21 19 i+ 21 19 j− 19 7 k. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.3 THE DOT PRODUCT ¤ 23 44. |a| = √1 + 4 + 9 = √14 so the scalar projection of b onto a is compa b = a · b |a| = 5 + 0 − 3 √14 = 2 √14 while the vector projection of b onto a is proja b = √214 |aa| = √214 · √114 (i + 2j + 3k) = 1 7(i + 2j + 3k) = 1 7 i + 2 7 j + 3 7 k. 45. (ortha b) · a = (b − proja b) · a = b · a − (proja b) · a = b · a − a · b |a|2 a · a = b · a − a|a·|b2 |a|2 = b · a − a · b = 0. So they are orthogonal by (7). 46. Using the formula in Exercise 45 and the result of Exercise 40, we have ortha b = b − proja b =h2 3i − 14 17 56 17 = 20 17 − 17 5 . 47. compa b = a · b |a| = 2 ⇔ a · b = 2|a| = 2√10. If b = h1 2 3i, then we need 31 + 02 − 13 = 2√10. One possible solution is obtained by taking 1 = 0, 2 = 0, 3 = −2√10. In general, b = 3 − 2√10, , ∈ R. 48. (a) compa b = compb a ⇔ a · b |a| = b · a |b| ⇔ 1 |a| = 1 |b| or a · b = 0 ⇔ |b| = |a| or a · b = 0. That is, if a and b are orthogonal or if they have the same length. (b) proja b = projb a ⇔ a · b |a|2 a = b · a |b|2 b ⇔ a · b = 0 or |aa|2 = |bb|2 . But a |a|2 = b |b|2 ⇒ |a| |a|2 = |b| |b|2 ⇒ |a| = |b|. Substituting this into the previous equation gives a = b. So proja b = projb a ⇔ a and b are orthogonal, or they are equal. 49. The displacement vector is D = (6 − 0)i + (12 − 10)j + (20 − 8)k = 6i + 2j + 12k so, by Equation 12, the work done is = F · D = (8i − 6j + 9k) · (6i + 2j + 12k) = 48 − 12 + 108 = 144 joules. 50. Here |D| = 1000 m, |F| = 1500 N, and = 30◦. Thus = F · D = |F| |D|cos = (1500)(1000) √23 = 750,000√3 joules. 51. Here |D| = 80 ft, |F| = 30 lb, and = 40◦. Thus = F · D = |F| |D|cos = (30)(80) cos 40◦ = 2400 cos 40◦ ≈ 1839 ft-lb. 52. = F · D = |F| |D|cos = (400)(120) cos 36◦ ≈ 38,833 ft-lb °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.24 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 53. First note that n = h i is perpendicular to the line, because if 1 = (1 1) and 2 = (2 2) lie on the line, then n · −−−→ 12 = 2 − 1 + 2 − 1 = 0, since 2 + 2 = − = 1 + 1 from the equation of the line. Let 2 = (2 2) lie on the line. Then the distance from 1 to the line is the absolute value of the scalar projection of −−−→ 12 onto n. compn − −− 1→2 = |n · h2 −|n1| 2 − 1i| = |2 − √12++ 22 − 1| = |√1 +2 +1+2 | since 2 + 2 = −. The required distance is |(3)(−2) + ( 32 + ( −−4)(3) + 5 4)2 | = 13 5 . 54. (r − a) · (r − b) = 0 implies that the vectors r − a and r − b are orthogonal. From the diagram (in which , and are the terminal points of the vectors), we see that this implies that lies on a sphere whose diameter is the line from to . The center of this circle is the midpoint of , that is, 1 2 (a + b) = 1 2(1 + 1) 1 2(2 + 2) 1 2(3 + 3), and its radius is 1 2 |a − b| = 1 2 (1 − 1)2 + (2 − 2)2 + (3 − 3)2. Or: Expand the given equation, substitute r · r = 2 + 2 + 2 and complete the squares. 55. For convenience, consider the unit cube positioned so that its back left corner is at the origin, and its edges lie along the coordinate axes. The diagonal of the cube that begins at the origin and ends at (1 11) has vector representation h1 1 1i. The angle between this vector and the vector of the edge which also begins at the origin and runs along the -axis [that is, h100i] is given by cos = h111i · h1 0 0i |h111i| |h1 0 0i| = 1 √ 3 ⇒ = cos−1 √13 ≈ 55◦. 56. Consider a cube with sides of unit length, wholly within the first octant and with edges along each of the three coordinate axes. i + j + k and i + j are vector representations of a diagonal of the cube and a diagonal of one of its faces. If is the angle between these diagonals, then cos = (i + j + k) · (i + j) |i + j + k| |i + j| = 1 + 1 √3√2 = 2 3 ⇒ = cos−1 2 3 ≈ 35◦. 57. Consider the H — C— H combination consisting of the sole carbon atom and the two hydrogen atoms that are at (1 0 0) and (010) (or any H— C— H combination, for that matter). Vector representations of the line segments emanating from the carbon atom and extending to these two hydrogen atoms are 1 − 1 2 0 − 1 20 − 1 2 = 1 2 − 1 2 − 1 2 and 0 − 1 21 − 1 2 0 − 1 2 = − 1 2 1 2 − 1 2. The bond angle, , is therefore given by cos = 1 2 − 1 2 − 1 2 · − 1 2 1 2 − 1 2 1 2 − 1 2 − 1 2 − 1 2 1 2 − 1 2 = − 1 4 − 1 4 + 1 4 3 4 3 4 = − 1 3 ⇒ = cos−1− 1 3 ≈ 1095◦. 58. Let be the angle between a and c and be the angle between c and b. We need to show that = . Now cos = a · c |a| |c| = a · |a|b + a · |b|a |a| |c| = |a|a · b + |a|2 |b| |a| |c| = a · b + |a| |b| |c| . Similarly, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.3 THE DOT PRODUCT ¤ 25 cos = b · c |b| |c| = |a| |b| + b · a |c| . Thus cos = cos. However 0◦ ≤ ≤ 180◦ and 0◦ ≤ ≤ 180◦, so = and c bisects the angle between a and b. 59. Let a = h1 2 3i and = h1 2 3i. Property 2: a · b = h1 2 3i · h1 2 3i = 11 + 22 + 33 = 11 + 22 + 33 = h1 2 3i · h1 2 3i = b · a Property 4: (a) · b = h1 2 3i · h1 2 3i = (1)1 + (2)2 + (3)3 = (11 + 22 + 33) = (a · b) = 1(1) + 2(2) + 3(3) = h1 2 3i · h1 2 3i = a · (b) Property 5: 0 · a = h0 0 0i · h1 2 3i = (0)(1) + (0)(2) + (0)(3) = 0 60. Let the figure be called quadrilateral . The diagonals can be represented by −→ and −−→ . −→ = −→ + −−→ and −−→ = −−→ + −−→ = −−→ − −−→ = −−→ − −→ (Since opposite sides of the object are of the same length and parallel, −→ = −−→ .) Thus −→ · −−→ = −→ + −−→ · −−→ − −→ = −→ · −− → − −→ + −−→ · −−→ − −→ = −→ · −−→ − −→ 2 + −−→ 2 − −→ · −−→ = −−→ 2 − −→ 2 But −→ 2 = −−→ 2 because all sides of the quadrilateral are equal in length. Therefore −→ · −−→ = 0, and since both of these vectors are nonzero this tells us that the diagonals of the quadrilateral are perpendicular. 61. |a · b| = |a| |b|cos = |a| |b| |cos|. Since |cos| ≤ 1, |a · b| = |a| |b| |cos | ≤ |a| |b|. Note: We have equality in the case of cos = ±1, so = 0 or = , thus equality when a and b are parallel. 62. (a) The Triangle Inequality states that the length of the longest side of a triangle is less than or equal to the sum of the lengths of the two shortest sides. (b) |a + b|2 = (a + b) · (a + b) = (a · a) + 2(a · b) + (b · b) = |a|2 + 2(a · b) + |b|2 ≤ |a|2 + 2|a| |b| + |b|2 [by the Cauchy-Schwartz Inequality] = (|a| + |b|)2 Thus, taking the square root of both sides, |a + b| ≤ |a| + |b|. 63. (a) The Parallelogram Law states that the sum of the squares of the lengths of the diagonals of a parallelogram equals the sum of the squares of its (four) sides. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.26 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE (b) |a + b|2 = (a + b) · (a + b) = |a|2 + 2(a · b) + |b|2 and |a − b|2 = (a − b) · (a − b) = |a|2 − 2(a · b) + |b|2. Adding these two equations gives |a + b|2 + |a − b|2 = 2|a|2 + 2|b|2. 64. If the vectors u + v and u − v are orthogonal then (u + v) · (u − v) = 0. But (u + v) · (u − v) = (u + v) · u − (u + v) · v by Property 3 of the dot product = u · u + v · u − u · v − v · v by Property 3 = |u|2 + u · v − u · v − |v|2 by Properties 1 and 2 = |u|2 − |v|2 Thus |u|2 − |v|2 = 0 ⇒ |u|2 = |v|2 ⇒ |u| = |v| [since |u|, |v| ≥ 0]. 65. proja b · projb a = a · b |a|2 a · b · a |b|2 b = a|a·|b2 · b|b·|2a (a · b) by Property 4 of the dot product = (a · b)2 |a|2 |b|2 (a · b) = |aa| | · bb|2 (a · b) by Property 2 = (cos)2 (a · b) = (a · b)cos2 by Corollary 6 12.4 The Cross Product 1. a × b = i j k 2 3 0 1 0 5 = 3 0 0 5 i − 2 0 1 5 j + 2 3 1 0 k = (15 − 0)i − (10 − 0)j + (0 − 3)k = 15i − 10j − 3k Now (a × b) · a = h15 −10 −3i · h230i = 30 − 30 + 0 = 0 and (a × b) · b = h15 −10 −3i · h105i = 15 + 0 − 15 = 0, so a × b is orthogonal to both a and b. 2. a × b = i j k 4 3 −2 2 −1 1 = 3 −2 −1 1 i − 4 −2 2 1 j + 4 3 2 −1 k = (3 − 2)i − [4 − (−4)]j + (−4 − 6)k = i − 8j − 10k Now (a × b) · a = h1 −8 −10i · h4 3 −2i = 4 − 24 + 20 = 0 and (a × b) · b = h1 −8 −10i · h2 −1 1i = 2 + 8 − 10 = 0, so a × b is orthogonal to both a and b. 3. a × b = i j k 0 2 −4 −1 3 1 = 2 −4 3 1 i − 0 −4 −1 1 j + 0 2 −1 3 k = [2 − (−12)]i − (0 − 4)j + [0 − (−2)]k = 14i + 4j + 2k Since (a × b) · a = (14i + 4j + 2k) · (2j − 4k) = 0 + 8 − 8 = 0, a × b is orthogonal to a. Since (a × b) · b = (14i + 4j + 2k) · (−i + 3j + k) = −14 + 12 + 2 = 0, a × b is orthogonal to b. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.4 THE CROSS PRODUCT ¤ 27 4. a × b = i j k 3 3 −3 3 −3 3 = 3 −3 −3 3 i − 3 −3 3 3 j + 3 3 3 −3 k = (9 − 9)i − [9 − (−9)]j + (−9 − 9)k = −18j − 18k Since (a × b) · a = (−18j − 18k) · (3i + 3j − 3k) = 0 − 54 + 54 = 0, a × b is orthogonal to a. Since (a × b) · b = (−18j − 18k) · (3i − 3j + 3k) = 0 + 54 − 54 = 0, a × b is orthogonal to b. 5. a × b = i j k 1 2 1 3 1 4 1 2 −3 = 1 3 1 4 2 −3 i − 1 2 1 4 1 −3 j + 1 2 1 3 1 2 k = −1 − 1 2i − − 3 2 − 1 4j + 1 − 1 3k = − 3 2 i + 7 4 j + 2 3 k Since (a × b) · a = − 3 2 i + 7 4 j + 2 3 k · 1 2 i + 1 3 j + 1 4 k = − 3 4 + 12 7 + 1 6 = 0, a × b is orthogonal to a. Since (a × b) · b = − 3 2 i + 7 4 j + 2 3 k · (i + 2j − 3k) = − 3 2 + 7 2 − 2 = 0, a × b is orthogonal to b. 6. a × b = i j k cos sin 1 −sin cos = cos sin −sin cos i − sin 1 cos j + cos 1 −sin k = [cos2 − (−sin2 )]i − (cos − sin)j + (−sin − cos)k = i + (sin − cos )j + (−sin − cos)k Since (a × b) · a = [i + (sin − cos)j + (−sin − cos )k] · (i + cosj + sink) = + sincos − cos2 − sin2 − sincos = − cos2 + sin2 = 0 a × b is orthogonal to a. Since (a × b) · b = [i + (sin − cos)j + (−sin − cos)k] · (i − sinj + cosk) = 1 − sin2 + sincos − sincos − cos2 = 1 − sin2 + cos2 = 0 a × b is orthogonal to b. 7. a × b = i j k 1 1 2 2 1 = 1 1 2 1 i − 1 2 1 j + 1 2 2 k = (1 − )i − ( − )j + (3 − 2)k = (1 − )i + (3 − 2)k Since (a × b) · a = 1 − 0 3 − 2 · h11i = − 2 + 0 + 2 − = 0, a × b is orthogonal to a. Since (a × b) · b = 1 − 0 3 − 2 · 2 21 = 2 − 3 + 0 + 3 − 2 = 0, a × b is orthogonal to b. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.28 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 8. a × b = i j k 1 0 −2 0 1 1 = 0 −2 1 1 i − 1 −2 0 1 j + 1 0 0 1 k = 2i − j + k 9. According to the discussion following Example 4, i × j = k, so (i × j) × k = k × k = 0 [by Example 2]. 10. k × (i − 2j) = k × i + k × (−2j) by Property 3 of the cross product = k × i + (−2) (k × j) by Property 2 = j + (−2)(−i) = 2i + j by the discussion following Example 4 11. (j − k) × (k − i) = (j − k) × k + (j − k) × (−i) by Property 3 of the cross product = j × k + (−k) × k + j × (−i) + (−k) × (−i) by Property 4 = (j × k) + (−1)(k × k) + (−1)(j × i) + (−1)2(k × i) by Property 2 = i + (−1)0 + (−1)(−k) + j = i + j + k by Example 2 and the discussion following Example 4 12. (i + j) × (i − j) = (i + j) × i + (i + j) × (−j) by Property 3 of the cross product = i × i + j × i + i × (−j) + j × (−j) by Property 4 = (i × i) + (j × i) + (−1)(i × j) + (−1)(j × j) by Property 2 = 0 + (−k) + (−1)k + (−1)0 = −2k by Example 2 and the discussion following Example 4 13. (a) Since b × c is a vector, the dot product a · (b × c) is meaningful and is a scalar. (b) b · c is a scalar, so a × (b · c) is meaningless, as the cross product is defined only for two vectors. (c) Since b × c is a vector, the cross product a × (b × c) is meaningful and results in another vector. (d) b · c is a scalar, so the dot product a · (b · c) is meaningless, as the dot product is defined only for two vectors. (e) Since (a · b) and (c · d) are both scalars, the cross product (a · b) × (c · d) is meaningless. (f) a × b and c × d are both vectors, so the dot product (a × b) · (c × d) is meaningful and is a scalar. 14. Using Theorem 9, we have |u × v| = |u| |v|sin = (4)(5) sin 45◦ = 20 · √2 2 = 10√2. By the right-hand rule, u × v is directed out of the page. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.4 THE CROSS PRODUCT ¤ 29 15. If we sketch u and v starting from the same initial point, we see that the angle between them is 60◦. Using Theorem 9, we have |u × v| = |u| |v|sin = (12)(16) sin 60◦ = 192 · √3 2 = 96√3. By the right-hand rule, u × v is directed into the page. 16. (a) |a × b| = |a| |b|sin = 3 · 2 · sin 2 = 6 (b) a × b is orthogonal to k, so it lies in the -plane, and its -coordinate is 0. By the right-hand rule, its -component is negative and its -component is positive. 17. a×b = i j k 2 −1 3 4 2 1 = −1 3 2 1 i − 2 3 4 1 j + 2 −1 4 2 k = (−1−6)i−(2−12)j+[4−(−4)]k = −7i+10j+8k b×a = i j k 4 2 1 2 −1 3 = 2 1 −1 3 i − 4 1 2 3 j + 4 2 2 −1 k = [6−(−1)]i−(12−2)j+(−4−4)k = 7i−10j−8k Notice a × b = −b × a here, as we know is always true by Property 1 of the cross product. 18. b × c = i j k 2 1 −1 0 1 3 = 1 −1 1 3 i − 2 −1 0 3 j + 2 1 0 1 k = 4i − 6j + 2k so a × (b × c) = i j k 1 0 1 4 −6 2 = 0 1 −6 2 i − 1 1 4 2 j + 1 0 4 −6 k = 6i + 2j − 6k. a × b = i j k 1 0 1 2 1 −1 = 0 1 1 −1 i − 1 1 2 −1 j + 1 0 2 1 k = − i + 3j + k so (a × b) × c = i j k −1 3 1 0 1 3 = 3 1 1 3 i − −1 1 0 3 j + −1 3 0 1 k = 8i + 3j − k. Thus a × (b × c) 6= (a × b) × c. 19. By Theorem 8, the cross product of two vectors is orthogonal to both vectors. So we calculate h321i × h−110i = i j k 3 2 1 −1 1 0 = 2 1 1 0 i − 3 1 −1 0 j + 3 2 −1 1 k = −i − j + 5k. So two unit vectors orthogonal to both given vectors are ±√h−1 + 1 + 25 1 −15i = ±h−13√−31 5i, that is, − 3√1 3 − 3√1 3 3√5 3 and 3√1 3 3√1 3 − 3√5 3. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.30 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 20. By Theorem 8, the cross product of two vectors is orthogonal to both vectors. So we calculate (j − k) × (i + j) = i j k 0 1 −1 1 1 0 = 1 −1 1 0 i − 0 −1 1 0 j + 0 1 1 1 k = i − j − k Thus two unit vectors orthogonal to both given vectors are ± √13(i − j − k), that is, √13 i − √13 j − √13 k and − 1√ 3 i + √13 j + √13 k. 21. Let a = h1 2 3i. Then 0 × a = i j k 0 0 0 1 2 3 = 0 0 2 3 i − 0 0 1 3 j + 0 0 1 2 k = 0, a × 0 = i j k 1 2 3 0 0 0 = 2 3 0 0 i − 1 3 0 0 j + 1 2 0 0 k = 0. 22. Let a = h1 2 3i and b = h1 2 3i. (a × b) · b = 22 33 11 33 11 22 · h1 2 3i = 22 33 1 − 11 33 2 + 11 22 3 = (231 − 321) − (132 − 312) + (123 − 213) = 0 23. a × b = h23 − 32 31 − 13 12 − 21i = h(−1)(23 − 32) (−1)(31 − 13)(−1)(12 − 21)i = − h23 − 32 31 − 13 12 − 21i = −b × a 24. a = h1 2 3i, so (a) × b = h23 − 32 31 − 13 12 − 21i = h23 − 32 31 − 13 12 − 21i = (a × b) = h23 − 32 31 − 13 12 − 21i = h2(3) − 3(2) 3(1) − 1(3) 1(2) − 2(1)i = a × b 25. a × (b + c) = a × h1 + 1 2 + 2 3 + 3i = h2(3 + 3) − 3(2 + 2), 3(1 + 1) − 1(3 + 3), 1(2 + 2) − 2(1 + 1)i = h23 + 23 − 32 − 32, 31 + 31 − 13 − 13, 12 + 12 − 21 − 21i = h(23 − 32) + (23 − 32), (31 − 13) + (31 − 13), (12 − 21) + (12 − 21)i = h23 − 32 31 − 13 12 − 21i + h23 − 32 31 − 13 12 − 21i = (a × b) + (a × c) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.4 THE CROSS PRODUCT ¤ 31 26. (a + b) × c = −c × (a + b) by Property 1 of the cross product = −(c × a + c × b) by Property 3 = −(−a × c + (−b × c)) by Property 1 = a × c + b × c by Property 2 27. By plotting the vertices, we can see that the parallelogram is determined by the vectors −→ = h23i and −−→ = h6 −1i. We know that the area of the parallelogram determined by two vectors is equal to the length of the cross product of these vectors. In order to compute the cross product, we consider the vector −→ as the three-dimensional vector h2 3 0i (and similarly for −−→ ), and then the area of parallelogram is −→ × −−→ = i j k 2 3 0 6 −1 0 = |(0 − 0)i − (0 − 0)j + (−2 − 18)k| = |−20k| = 20 28. By plotting the vertices, we can see that the parallelogram is determined by the vectors −−→ = h231i and −→ = h425i. Thus the area of parallelogram is −−→ × −→ = i j k 2 3 1 4 2 5 = |(15 − 2)i − (10 − 4)j + (4 − 12)k| = |13i − 6j − 8k| = √169 + 36 + 64 = √269 ≈ 1640 29. (a) Because the plane through , , and contains the vectors −−→ and −→ , a vector orthogonal to both of these vectors (such as their cross product) is also orthogonal to the plane. Here −−→ = h−3 12i and −→ = h324i, so −−→ × −→ = h(1)(4) − (2)(2)(2)(3) − (−3)(4)(−3)(2) − (1)(3)i = h018 −9i Therefore, h0 18 −9i (or any nonzero scalar multiple thereof, such as h0 2 −1i) is orthogonal to the plane through , , and . (b) Note that the area of the triangle determined by , , and is equal to half of the area of the parallelogram determined by the three points. From part (a), the area of the parallelogram is −−→ × −→ = |h018 −9i| = √0 + 324 + 81 = √405 = 9√5, so the area of the triangle is 1 2 · 9√5 = 9 2√5. 30. (a) −−→ = h423i and −→ = h334i, so a vector orthogonal to the plane through , , and is −−→ × −→ = h(2)(4) − (3)(3)(3)(3) − (4)(4)(4)(3) − (2)(3)i = h−1 −76i (or any nonzero scalar mutiple thereof). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.32 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE (b) The area of the parallelogram determined by −−→ and −→ is −−→ × −→ = |h−1 −76i| = √1 + 49 + 36 = √86, so the area of triangle is 1 2√86. 31. (a) −−→ = h4 3 −2i and −→ = h5 5 1i, so a vector orthogonal to the plane through , , and is −−→ × −→ = h(3)(1) − (−2)(5)(−2)(5) − (4)(1) (4)(5) − (3)(5)i = h13 −14 5i [or any scalar mutiple thereof]. (b) The area of the parallelogram determined by −−→ and −→ is −−→ × −→ = |h13 −145i| = 132 + (−14)2 + 52 = √390, so the area of triangle is 1 2√390. 32. (a) −−→ = h−3 1 −2i and −→ = h14 −7i, so a vector orthogonal to the plane through , , and is −−→ × −→ = h(1)(−7) − (−2)(4)(−2)(1) − (−3)(−7) (−3)(4) − (1)(1)i = h1 −23 −13i [or any scalar multiple thereof]. (b) The area of the parallelogram determined by −−→ and −→ is −−→ × −→ = |h1 −23 −13i| = √1 + 529 + 169 = √699, so the area of triangle is 1 2 √699. 33. By Equation 14, the volume of the parallelepiped determined by a, b, and c is the magnitude of their scalar triple product, which is a · (b × c) = 1 2 3 −1 1 2 2 1 4 = 1 1 2 1 4 − 2 −1 2 2 4 + 3 −1 1 2 1 = 1(4 − 2) − 2(−4 − 4) + 3(−1 − 2) = 9. Thus the volume of the parallelepiped is 9 cubic units. 34. a · (b × c) = 1 1 0 0 1 1 1 1 1 = 1 1 1 1 1 − 1 0 1 1 1 + 0 0 1 1 1 = 0 + 1 + 0 = 1. So the volume of the parallelepiped determined by a, b, and c is 1 cubic unit. 35. a = −−→ = h422i, b = −→ = h33 −1i, and c = −→ = h551i. a · (b × c) = 4 2 2 3 3 −1 5 5 1 = 4 3 −1 5 1 − 2 3 −1 5 1 + 2 3 3 5 5 = 32 − 16 + 0 = 16, so the volume of the parallelepiped is 16 cubic units. 36. a = −−→ = h−424i, b = −→ = h21 −2i and c = −→ = h−341i. a · (b × c) = −4 2 4 2 1 −2 −3 4 1 = −4 1 −2 4 1 − 2 2 −2 −3 1 + 4 2 1 −3 4 = −36 + 8 + 44 = 16, so the volume of the parallelepiped is 16 cubic units. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.4 THE CROSS PRODUCT ¤ 33 37. u · (v × w) = 1 5 −2 3 −1 0 5 9 −4 = 1 −1 0 9 −4 − 5 3 0 5 −4 + (−2) 3 −1 5 9 = 4 + 60 − 64 = 0, which says that the volume of the parallelepiped determined by u, v and w is 0, and thus these three vectors are coplanar. 38. u = −→ = h2 −44i, v = −→ = h4 −1 −2i and w = −−→ = h23 −6i. u · (v × w) = 2 −4 4 4 −1 −2 2 3 −6 = 2 −1 −2 3 −6 − (−4) 4 −2 2 −6 + 4 4 −1 2 3 = 24 − 80 + 56 = 0, so the volume of the parallelepiped determined by u, v and w is 0, which says these vectors lie in the same plane. Therefore, their initial and terminal points , , and also lie in the same plane. 39. Using the notation of the text, |r| = 018 m, |F| = 60 N, and the angle between r and F is = 70◦ + 10◦ = 80◦. (Move F so that both vectors start from the same point.) Then the magnitude of the torque is || = |r × F| = |r| |F|sin = (018)(60) sin 80◦ = 108sin 80◦ ≈ 106 N·m. 40. (a) The position vector from the point to the handle is r = h12i and has magnitude |r| = √12 + 22 = √5 ft. Since the force vector F is parallel to the -axis, the angle between r and F is = tan−1 2 1 ≈ 6343◦ and the magnitude of the torque is || = |r × F| = |r| |F|sin ≈ √5(20)sin6343◦ ≈ 400 ft-lb. (Alternatively, we can observe that sin = √25 , so |r| |F| sin = √5 · 20 · √25 = 40.) (b) In this case r = −−→ = h0606i, so |r| = (06)2 + (06)2 = √072 and = 45◦. The magnitude of the torque is || = |r| |F|sin = √072(20)sin45◦ = √072(20) · √22 = 10√144 = 12 ft-lb. 41. Using the notation of the text, r = h0030i (measuring in meters) and F has direction h03 −4i. The angle between them can be determined by cos = h0030i · h03 −4i |h0030i| |h03 −4i| ⇒ cos = (003)(5) 9 ⇒ cos = 06 ⇒ = cos−1(06) ≈ 531◦. Then || = |r| |F|sin ⇒ 100 ≈ 03|F|sin531◦ ⇒ |F| ≈ 100 03sin531◦ ≈ 417 N. 42. Since |u × v| = |u| |v|sin, 0 ≤ ≤ , |u × v| achieves its maximum value for sin = 1 ⇒ = 2 , in which case |u × v| = |u| |v| = 15 The minimum value is zero, which occurs when sin = 0 ⇒ = 0 or , so when u, v are parallel. Thus, when u points in the same direction as v, so u = 3j, |u × v| = 0. As u rotates counterclockwise, u × v is directed in the negative -direction (by the right-hand rule) and the length increases until = 2 , in which case u = −3i and |u × v| = 15. As u rotates to the negative -axis, u × v remains pointed in the negative -direction and the length of u × v decreases to 0 after which the direction of u × v reverses to point in the positive -direction and |u × v| increases. When u = 3i (so = 2 ), |u × v| again reaches its maximum of 15, after which |u × v| decreases to 0 as u rotates to the positive -axis. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.34 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 43. From Theorem 9 we have |a × b| = |a| |b|sin, where is the angle between a and b, and from Theorem 12.3.3 we have a · b = |a| |b| cos ⇒ |a| |b| = a · b cos . Substituting the second equation into the first gives |a × b| = cos a · b sin, so |a × b| a · b = tan. Here |a × b| = |h12 2i| = √1 + 4 + 4 = 3, so tan = |aa×· bb| = √33 = √3 ⇒ = 60◦. 44. (a) Let v = h1 23i. Then h121i ×v = i j k 1 2 1 1 2 3 = 2 1 2 3 i − 1 1 1 3 j + 1 2 1 2 k = (23 − 2)i − (3 − 1)j + (2 − 21)k. If h121i × v = h3 1 −5i then h23 − 2 1 − 3 2 − 21i = h31 −5i ⇔ 23 − 2 = 3 (1), 1 − 3 = 1 (2), and 2 − 21 = −5 (3). From (3) we have 2 = 21 − 5 and from (2) we have 3 = 1 − 1; substitution into (1) gives 2(1 − 1) − (21 − 5) = 3 ⇒ 3 = 3, so this is a dependent system. If we let 1 = then 2 = 2 − 5 and 3 = − 1, so v is any vector of the form h2 − 5 − 1i. (b) If h121i × v = h3 1 5i then 23 − 2 = 3 (1), 1 − 3 = 1 (2), and 2 − 21 = 5 (3). From (3) we have 2 = 21 + 5 and from (2) we have 3 = 1 − 1; substitution into (1) gives 2(1 − 1) − (21 + 5) = 3 ⇒ −7 = 3, so this is an inconsistent system and has no solution. Alternatively, if we use matrices to solve the system we could show that the determinant is 0 (and hence the system has no solution). 45. (a) The distance between a point and a line is the length of the perpendicular from the point to the line, here −→ = . But referring to triangle , = −→ = −−→ sin = |b|sin. But is the angle between −−→ = b and −→ = a. Thus by Theorem 9, sin = |a × b| |a| |b| and so = |b|sin = |b| |a × b| |a| |b| = |a × b| |a| . (b) a = −→ = h−1 −2 −1i and b = −−→ = h1 −5 −7i. Then a × b = h(−2)(−7) − (−1)(−5) (−1)(1) − (−1)(−7)(−1)(−5) − (−2)(1)i = h9 −87i. Thus the distance is = |a × b| |a| = 1√ 6 √81 + 64 + 49 = 194 6 = 97 3 . 46. (a) The distance between a point and a plane is the length of the perpendicular from the point to the plane, here −→ = . But −→ is parallel to b × a (because b × a is perpendicular to b and a) and = −→ = the absolute value of the scalar projection of c along b × a, which is |c| |cos |. (Notice that this is the same °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.4 THE CROSS PRODUCT ¤ 35 setup as the development of the volume of a parallelepiped with = |c| |cos|). Thus = |c| |cos| = = where = |a × b|, the area of the base. So finally = = |a · (b × c)| |a × b| . (b) a = −→ = h−120i, b = −→ = h−103i and c = −−→ = h114i. Then a · (b × c) = −1 2 0 −1 0 3 1 1 4 = (−1) 0 3 1 4 − 2 −1 3 1 4 + 0 = 17 and a × b = i j k −1 2 0 −1 0 3 = 2 0 0 3 i − −1 0 −1 3 j + −1 2 −1 0 k = 6i + 3j + 2k Thus = |a · (b × c)| |a × b| = 17 √36 + 9 + 4 = 17 7 . 47. From Theorem 9 we have |a × b| = |a| |b|sin so |a × b|2 = |a|2 |b|2 sin2 = |a|2 |b|2 1 − cos2 = |a|2 |b|2 − (|a| |b|cos)2 = |a|2 |b|2 − (a · b)2 by Theorem 12.3.3. 48. If a + b + c = 0 then b = −(a + c), so a × b = a × [−(a + c)] = −[a × (a + c)] by Property 2 of the cross product (with = −1) = −[(a × a) + (a × c)] by Property 3 = −[0 + (a × c)] = −a × c by Example 2 = c × a by Property 1 Similarly, a = −(b + c) so c × a = c × [−(b + c)] = −[c × (b + c)] = −[(c × b) + (c × c)] = −[(c × b) + 0] = −c × b = b × c Thus a × b = b × c = c × a. 49. (a − b) × (a + b) = (a − b) × a + (a − b) × b by Property 3 of the cross product = a × a + (−b) × a + a × b + (−b) × b by Property 4 = (a × a) − (b × a) + (a × b) − (b × b) by Property 2 (with = −1) = 0 − (b × a) + (a × b) − 0 by Example 2 = (a × b) + (a × b) by Property 1 = 2(a × b) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.36 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 50. Let a = h1 2 3i, b = h1 2 3i and c = h1 2 3i, so b × c = h23 − 32 31 − 13 12 − 21i and a × (b × c) = h2(12 − 21) − 3(31 − 13), 3(23 − 32) − 1(12 − 21), 1(31 − 13) − 2(23 − 32)i = h212 − 221 − 331 + 313, 323 − 332 − 112 + 121 131 − 113 − 223 + 232i = h(22 + 33)1 − (22 + 33)1, (11 + 33)2 − (11 + 33)2, (11 + 22)3 − (11 + 22)3i () = h(22 + 33)1 − (22 + 33)1 + 111 − 111, (11 + 33)2 − (11 + 33)2 + 222 − 222, (11 + 22)3 − (11 + 22)3 + 333 − 333i = h(11 + 22 + 33)1 − (11 + 22 + 33)1, (11 + 22 + 33)2 − (11 + 22 + 33)2, (11 + 22 + 33)3 − (11 + 22 + 33)3i = (11 + 22 + 33)h1 2 3i − (11 + 22 + 33)h1 2 3i = (a · c)b − (a · b)c () Here we look ahead to see what terms are still needed to arrive at the desired equation. By adding and subtracting the same terms, we don’t change the value of the component. 51. a × (b × c) + b × (c × a) + c × (a × b) = [(a · c)b − (a · b)c] + [(b · a)c − (b · c)a] + [(c · b)a − (c · a)b] by Exercise 50 = (a · c)b − (a · b)c + (a · b)c − (b · c)a + (b · c)a − (a · c)b = 0 52. Let c × d = v. Then (a × b) · (c × d) = (a × b) · v = a · (b × v) by Property 5 of the cross product = a · [b × (c × d)] = a · [(b · d)c − (b · c)d] by Exercise 50 = (b · d)(a · c) − (b · c)(a · d) by Properties 3 and 4 of the dot product = a · c b · c a · d b · d 53. (a) No. If a · b = a · c, then a · (b − c) = 0, so a is perpendicular to b − c, which can happen if b 6= c. For example, let a = h1 1 1i, b = h1 0 0i and c = h010i. (b) No. If a × b = a × c then a × (b − c) = 0, which implies that a is parallel to b − c, which of course can happen if b 6= c. (c) Yes. Since a · c = a · b, a is perpendicular to b − c, by part (a). From part (b), a is also parallel to b − c. Thus since a 6= 0 but is both parallel and perpendicular to b − c, we have b − c = 0, so b = c. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.DISCOVERY PROJECT THE GEOMETRY OF A TETRAHEDRON ¤ 37 54. (a) k is perpendicular to v if 6= by the definition of k and Theorem 8. (b) k1 · v1 = v2 × v3 v1 · (v2 × v3) · v1 = v1 · (v2 × v3) v1 · (v2 × v3) = 1 k2 · v2 = v3 × v1 v1 · (v2 × v3) · v2 = v2 · (v3 × v1) v1 · (v2 × v3) = (v2 × v3) · v1 v1 · (v2 × v3) = 1 [by Property 5 of the cross product] k3 · v3 = (v1 × v2) · v3 v1 · (v2 × v3) = v1 · (v2 × v3) v1 · (v2 × v3) = 1 [by Property 5] (c) k1 · (k2 × k3) = k1 · v1 v · (3v×2 ×v1v3) × v1 v· (1v×2 ×v2v3) = [v1 · (vk2 1× v3)]2 · [(v3 × v1) × (v1 × v2)] = k1 [v1 · (v2 × v3)]2 · ([(v3 × v1) · v2]v1 − [(v3 × v1) · v1]v2) [by Exercise 50] But (v3 × v1) · v1 = 0 since v3 × v1 is orthogonal to v1, and (v3 × v1) · v2 = v2 · (v3 × v1) = (v2 × v3) · v1 = v1 · (v2 × v3). Thus k1 · (k2 × k3) = k1 [v1 · (v2 × v3)]2 · [v1 · (v2 × v3)]v1 = v1 ·k(1v2· v×1v3) = v1 · (v12 × v3) [by part (b)] DISCOVERY PROJECT The Geometry of a Tetrahedron 1. Set up a coordinate system so that vertex is at the origin, = (0 10), = (2 20), = (3 3 3). Then −→ = h0 10i, −→ = h2 2 0i, −→ = h3 3 3i, −→ = h−2 1 − 2 0i, and −−→ = h3 − 2 3 − 2 3i. Let v = −→ × −−→ = (13 − 23)i + 23 j + (−23 − 31 + 32 + 21)k Then v is an outward normal to the face opposite vertex . Similarly, v = −→ × −→ = 23 i − 23 j + (23 − 32)k, v = −→ × −→ = −13 i + 31 k, and v = −→ × −→ = −21 k ⇒ v + v + v + v = 0. Now |v| = area of the parallelogram determined by −→ and −−→ = 2 (area of triangle ) = 2|v1| So v = 2v1, and similarly v = 2v2, v = 2v3, v = 2v4. Thus v1 + v2 + v3 + v4 = 0. 2. (a) Let = (0 0 0), = (1 1 1), = (2 2 2), = (3 3 3) be the four vertices. Then Volume = 1 3(distance from to plane ) × (area of triangle ) = 1 3 N · −→ |N| · 1 2 −→ × −→ °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.38 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE where N is a vector which is normal to the face . Thus N = −→ × −→ . Therefore = 1 6 −→ × −→ · −→ = 16 0 − 0 − 1 0 − 1 2 − 1 2 − 1 2 − 1 3 − 1 3 − 1 3 − 1 (b) Using the formula from part (a), = 1 6 1 − 1 1 − 2 1 − 3 1 − 1 1 − 2 2 − 3 3 − 1 −1 − 2 2 − 3 = 1 6 2(1 − 2) = 1 3 . 3. We define a vector v1 to have length equal to the area of the face opposite vertex , so we can say |v1| = , and direction perpendicular to the face and pointing outward, as in Problem 1. Similarly, we define v2, v3, and v4 so that |v2| = , |v3| = , and |v4| = and with the analogous directions. From Problem 1, we know v1 + v2 + v3 + v4 = 0 ⇒ v4 = −(v1 + v2 + v3) ⇒ |v4| = |−(v1 + v2 + v3)| = |v1 + v2 + v3| ⇒ |v4|2 = |v1 + v2 + v3|2 ⇒ v4 · v4 = (v1 + v2 + v3) · (v1 + v2 + v3) = v1 · v1 + v1 · v2 + v1 · v3 + v2 · v1 + v2 · v2 + v2 · v3 + v3 · v1 + v3 · v2 + v3 · v3 Since the vertex is trirectangular, we know the three faces meeting at are mutually perpendicular, so the vectors v1, v2, v3 are also mutually perpendicular. Therefore, v · v = 0 for 6= and , ∈ {123}. Thus we have v4 · v4 = v1 · v1 + v2 · v2 + v3 · v3 ⇒ |v4|2 = |v1|2 + |v2|2 + |v3|2 ⇒ 2 = 2 + 2 + 2. Another method: We introduce a coordinate system, as shown. Recall that the area of the parallelogram spanned by two vectors is equal to the length of their cross product, so since u × v = h− 0i × h−0 i = h i, we have |u × v| = ()2 + ()2 + ()2, and therefore 2 = 1 2|u × v|2 = 1 4[()2 + ()2 + ()2] = 1 22 + 1 22 + 1 22 = 2 + 2 + 2. A third method: We draw a line from perpendicular to , as shown. Now = 1 2, so 2 = 1 422. Substituting 2 = 2 + 2, we get 2 = 1 422 + 2 = 1 422 + 1 422. But = 1 2, so 2 = 1 422 + 2. Now substituting 2 = 2 + 2 gives 2 = 1 422 + 1 422 + 2 = 2 + 2 + 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.5 EQUATIONS OF LINES AND PLANES ¤ 39 12.5 Equations of Lines and Planes 1. (a) True; each of the first two lines has a direction vector parallel to the direction vector of the third line, so these vectors are each scalar multiples of the third direction vector. Then the first two direction vectors are also scalar multiples of each other, so these vectors, and hence the two lines, are parallel. (b) False; for example, the - and -axes are both perpendicular to the -axis, yet the - and -axes are not parallel. (c) True; each of the first two planes has a normal vector parallel to the normal vector of the third plane, so these two normal vectors are parallel to each other and the planes are parallel. (d) False; for example, the - and -planes are not parallel, yet they are both perpendicular to the -plane. (e) False; the - and -axes are not parallel, yet they are both parallel to the plane = 1. (f ) True; if each line is perpendicular to a plane, then the lines’ direction vectors are both parallel to a normal vector for the plane. Thus, the direction vectors are parallel to each other and the lines are parallel. (g) False; the planes = 1 and = 1 are not parallel, yet they are both parallel to the -axis. (h) True; if each plane is perpendicular to a line, then any normal vector for each plane is parallel to a direction vector for the line. Thus, the normal vectors are parallel to each other and the planes are parallel. (i) True; see Figure 9 and the accompanying discussion. ( j) False; they can be skew, as in Example 3. (k) True. Consider any normal vector for the plane and any direction vector for the line. If the normal vector is perpendicular to the direction vector, the line and plane are parallel. Otherwise, the vectors meet at an angle , 0◦ ≤ 90◦, and the line will intersect the plane at an angle 90◦ − . 2. For this line, we have r0 = 6i − 5j + 2k and v = i + 3j − 2 3 k, so a vector equation is r = r0 + v = (6i − 5j + 2k) + i + 3j − 2 3 k = (6 + )i + (−5 + 3)j + 2 − 2 3k and parametric equations are = 6 + , = −5 + 3, = 2 − 2 3. 3. For this line, we have r0 = 2i + 24j + 35k and v = 3i + 2j − k, so a vector equation is r = r0 + v = (2i+ 24j+ 35k) + (3i+ 2j−k) = (2 + 3)i+ (24 + 2)j+ (35 − )k and parametric equations are = 2 + 3, = 24 + 2, = 35 − . 4. This line has the same direction as the given line, v = 2i − 3j + 9k. Here r0 = 14j − 10k, so a vector equation is r = (14j − 10k) + (2i − 3j + 9k) = 2i + (14 − 3)j + (−10 + 9)k and parametric equations are = 2, = 14 − 3, = −10 + 9. 5. A line perpendicular to the given plane has the same direction as a normal vector to the plane, such as n = h1 3 1i. So r0 = i + 6k, and we can take v = i + 3j + k. Then a vector equation is r = (i + 6k) + (i + 3j + k) = (1 + )i + 3j + (6 + )k, and parametric equations are = 1 + , = 3, = 6 + . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.40 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 6. The vector v = h4 − 03 − 0 −1 − 0i = h4 3 −1i is parallel to the line. Letting 0 = (0 0 0), parametric equations are = 0 + 4 · = 4, = 0 + 3 · = 3, = 0 + (−1) · = −, while symmetric equations are 4 = 3 = − 1 or 4 = 3 = −. 7. The vector v = 2 − 0 1 − 1 2 −3 − 1 = 2 1 2 −4 is parallel to the line. Letting 0 = (21 −3), parametric equations are = 2 + 2, = 1 + 1 2, = −3 − 4, while symmetric equations are −2 2 = 1−21 = −+ 3 4 or − 2 2 = 2 − 2 = + 3 −4 . 8. v = h26 − 112 − 2403 − 46i = h16 −12 −43i, and letting 0 = (12446), parametric equations are = 1 + 16, = 24 − 12, = 46 − 43, while symmetric equations are − 1 16 = − 24 −12 = − 46 −43 . 9. v = h3 − (−8) −2 − 14 − 4i = h11 −30i, and letting 0 = (−814), parametric equations are = −8 + 11, = 1 − 3, = 4 + 0 = 4, while symmetric equations are + 8 11 = − 1 −3 , = 4. Notice here that the direction number = 0, so rather than writing − 4 0 in the symmetric equation we must write the equation = 4 separately. 10. v = (i + j) × (j + k) = i j k 1 1 0 0 1 1 = i − j + k is the direction of the line perpendicular to both i + j and j + k. With 0 = (210), parametric equations are = 2 + , = 1 − , = and symmetric equations are − 2 = − 1 −1 = or − 2 = 1 − = . 11. The given line 2 = 3 = + 1 1 has direction v = h2 3 1i. Taking (−62 3) as 0, parametric equations are = −6 + 2, = 2 + 3, = 3 + and symmetric equations are + 6 2 = − 2 3 = − 3. 12. Setting = 0 we see that (100) satisfies the equations of both planes, so they do in fact have a line of intersection. The line is perpendicular to the normal vectors of both planes, so a direction vector for the line is v = n1 × n2 = h123i × h1 −11i = h52 −3i. Taking the point (100) as 0, parametric equations are = 1 + 5, = 2, = −3, and symmetric equations are − 1 5 = 2 = −3 . 13. Direction vectors of the lines are v1 = h−2 − (−4) 0 − (−6) −3 − 1i = h26 −4i and v2 = h5 − 103 − 1814 − 4i = h−5 −1510i, and since v2 = − 5 2v1, the direction vectors and thus the lines are parallel. 14. Direction vectors of the lines are v1 = h3 −31i and v2 = h1 −4 −12i. Since v1 · v2 = 3 + 12 − 12 6= 0, the vectors and thus the lines are not perpendicular. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.5 EQUATIONS OF LINES AND PLANES ¤ 41 15. (a) The line passes through the point (1 −56) and a direction vector for the line is h−12 −3i, so symmetric equations for the line are − 1 −1 = + 5 2 = − 6 −3 . (b) The line intersects the -plane when = 0, so we need − 1 −1 = + 5 2 = 0 − 6 −3 or − 1 −1 = 2 ⇒ = −1, + 5 2 = 2 ⇒ = −1. Thus the point of intersection with the -plane is (−1 −1 0). Similarly for the -plane, we need = 0 ⇒ 1 = + 5 2 = − 6 −3 ⇒ = −3, = 3. Thus the line intersects the -plane at (0 −3 3). For the -plane, we need = 0 ⇒ − 1 −1 = 5 2 = − 6 −3 ⇒ = − 3 2, = − 3 2. So the line intersects the -plane at − 3 20 − 3 2 . 16. (a) A vector normal to the plane − + 3 = 7 is n = h1 −1 3i, and since the line is to be perpendicular to the plane, n is also a direction vector for the line. Thus parametric equations of the line are = 2 + , = 4 − , = 6 + 3. (b) On the -plane, = 0. So = 6 + 3 = 0 ⇒ = −2 in the parametric equations of the line, and therefore = 0 and = 6, giving the point of intersection (060). For the -plane, = 0 so we get the same point of interesection: (060). For the -plane, = 0 which implies = 4, so = 6 and = 18 and the point of intersection is (6018). 17. From Equation 4, the line segment from r0 = 6i − j + 9k to r1 = 7i + 6j has vector equation r() = (1 − )r0 + r1 = (1 − )(6i − j + 9k) + (7i + 6j) = (6i − j + 9k) − (6i − j + 9k) + (7i + 6j) = (6i − j + 9k) + (i + 7j − 9k), 0 ≤ ≤ 1. 18. From Equation 4, the line segment from r0 = −2i + 18j + 31k to r1 = 11i − 4j + 48k has vector equation r() = (1 − )r0 + r1 = (1 − )(−2i + 18j + 31k) + (11i − 4j + 48k) = (−2i + 18j + 31k) + (13i − 22j + 17k), 0 ≤ ≤ 1. The corresponding parametric equations are = −2 + 13, = 18 − 22, = 31 + 17, 0 ≤ ≤ 1. 19. Since the direction vectors h2 −1 3i and h4 −25i are not scalar multiples of each other, the lines aren’t parallel. For the lines to intersect, we must be able to find one value of and one value of that produce the same point from the respective parametric equations. Thus we need to satisfy the following three equations: 3 + 2 = 1 + 4, 4 − = 3 − 2, 1 + 3 = 4 + 5. Solving the last two equations we get = 1, = 0 and checking, we see that these values don’t satisfy the first equation. Thus the lines aren’t parallel and don’t intersect, so they must be skew lines. 20. Since the direction vectors are v1 = h−129 −3i and v2 = h8 −62i, we have v1 = − 3 2v2 so the lines are parallel. 21. Since the direction vectors h1 −2 −3i and h13 −7i aren’t scalar multiples of each other, the lines aren’t parallel. Parametric equations of the lines are 1: = 2 + , = 3 − 2, = 1 − 3 and 2: = 3 + , = −4 + 3, = 2 − 7. Thus, for the lines to intersect, the three equations 2 + = 3 + , 3 − 2 = −4 + 3, and 1 − 3 = 2 − 7 must be satisfied simultaneously. Solving the first two equations gives = 2, = 1 and checking, we see that these values do satisfy the third equation, so the lines intersect when = 2 and = 1, that is, at the point (4 −1 −5). °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.42 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 22. The direction vectors h1 −13i and h2 −2 7i are not parallel, so neither are the lines. Parametric equations for the lines are 1: = , = 1 − , = 2 + 3 and 2: = 2 + 2, = 3 − 2, = 7. Thus, for the lines to interesect, the three equations = 2 + 2, 1 − = 3 − 2, and 2 + 3 = 7 must be satisfied simultaneously. Solving the last two equations gives = −10, = −4 and checking, we see that these values don’t satisfy the first equation. Thus the lines aren’t parallel and don’t intersect, so they must be skew. 23. Since the plane is perpendicular to the vector h1 −25i, we can take h1 −2 5i as a normal vector to the plane. (000) is a point on the plane, so setting = 1, = −2, = 5 and 0 = 0, 0 = 0, 0 = 0 in Equation 7 gives 1( − 0) + (−2)( − 0) + 5( − 0) = 0 or − 2 + 5 = 0 as an equation of the plane. 24. 2i + j − k = h21 −1i is a normal vector to the plane and (5 3 5) is a point on the plane, so setting = 2, = 1, = −1 0 = 5, 0 = 3, 0 = 5 in Equation 7 gives 2( − 5) + 1( − 3) + (−1)( − 5) = 0 or 2 + − = 8 as an equation of the plane. 25. i + 4j + k = h1 4 1i is a normal vector to the plane and −1 1 23 is a point on the plane, so setting = 1, = 4, = 1 0 = −1, 0 = 1 2, 0 = 3 in Equation 7 gives 1[ − (−1)] + 4 − 1 2 + 1( − 3) = 0 or + 4 + = 4 as an equation of the plane. 26. Since the line is perpendicular to the plane, its direction vector h3 −1 4i is a normal vector to the plane. The point (201) is on the plane, so an equation of the plane is 3( − 2) + (−1)( − 0) + 4( − 1) = 0 or 3 − + 4 = 10. 27. Since the two planes are parallel, they will have the same normal vectors. So we can take n = h5 −1 −1i, and an equation of the plane is 5( − 1) − 1[ − (−1)] − 1[ − (−1)] = 0 or 5 − − = 7. 28. Since the two planes are parallel, they will have the same normal vectors. A normal vector for the plane = + or + − = 0 is n = h11 −1i, and an equation of the desired plane is 1( − 3) + 1[ − (−2)] − 1( − 8) = 0 or + − = −7. 29. Since the two planes are parallel, they will have the same normal vectors. So we can take n = h111i, and an equation of the plane is 1( − 1) + 1 − 1 2 + 1 − 1 3 = 0 or + + = 11 6 or 6 + 6 + 6 = 11. 30. First, a normal vector for the plane 5 + 2 + = 1 is n = h521i. A direction vector for the line is v = h1 −1 −3i, and since n · v = 0 we know the line is perpendicular to n and hence parallel to the plane. Thus, there is a parallel plane which contains the line. By putting = 0, we know that the point (124) is on the line and hence the new plane. We can use the same normal vector n = h5 2 1i, so an equation of the plane is 5( − 1) + 2( − 2) + 1( − 4) = 0 or 5 + 2 + = 13. 31. The vector from (011) to (1 0 1), namely a = h1 − 00 − 11 − 1i = h1 −10i, and the vector from (011) to (110), b = h1 − 01 − 10 − 1i = h10 −1i, both lie in the plane, so a × b is a normal vector to the plane. Thus, we can take n = a × b = h(−1)((−1) − (0)(0)(0)(1) − (1)(−1) (1)(0) − (−1)(1)i = h111i. If 0 is the point (011), an equation of the plane is 1( − 0) + 1( − 1) + 1( − 1) = 0 or + + = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.5 EQUATIONS OF LINES AND PLANES ¤ 43 32. Here the vectors a = h3 −21i and b = h111i lie in the plane, so n = a × b = h(−2)(1) − (1)(1)(1)(1) − (3)(1)(3)(1) − (−2)(1)i = h−3 −25i is a normal vector to the plane. We can take the origin as 0, so an equation of the plane is −3( − 0) − 2( − 0) + 5( − 0) = 0 or −3 − 2 + 5 = 0 or 3 + 2 − 5 = 0. 33. Here the vectors a = h3 − 2 −8 − 16 − 2i = h1 −9 4i and b = h−2 − 2 −3 − 1 1 − 2i = h−4 −4 −1i lie in the plane, so a normal vector to the plane is n = a × b = h9 + 16 −16 + 1 −4 − 36i = h25 −15 −40i and an equation of the plane is 25( − 2) − 15( − 1) − 40( − 2) = 0 or 25 − 15 − 40 = −45 or 5 − 3 − 8 = −9. 34. The vectors a = h−2 − 3 −2 − 0 3 − (−1)i = h−5 −2 4i and b = h7 − 3 1 − 0 −4 − (−1)i = h4 1 −3i lie in the plane, so a normal vector to the plane is n = a × b = h6 − 4 16 − 15 −5 + 8i = h213i and an equation of the plane is 2( − 3) + 1( − 0) + 3[ − (−1)] = 0 or 2 + + 3 = 3. 35. If we first find two nonparallel vectors in the plane, their cross product will be a normal vector to the plane. Since the given line lies in the plane, its direction vector a = h−12 −3i is one vector in the plane. We can verify that the given point (35 −1) does not lie on this line, so to find another nonparallel vector b which lies in the plane, we can pick any point on the line and find a vector connecting the points. If we put = 0, we see that (4 −10) is on the line, so b = h4 − 3 −1 − 5 0 − (−1)i = h1 −61i and n = a × b = h2 − 18 −3 + 16 − 2i = h−16 −2 4i. Thus, an equation of the plane is −16( − 3) − 2( − 5) + 4[ − (−1)] = 0 or −16 − 2 + 4 = −62 or 8 + − 2 = 31. 36. Since the line 3 = + 4 1 = 2 lies in the plane, its direction vector a = h3 1 2i is parallel to the plane. The point (0 −40) is on the line (put = 0 in the corresponding parametric equations), and we can verify that the given point (6 −1 3) in the plane is not on the line. The vector connecting these two points, b = h633i, is therefore parallel to the plane, but not parallel to a. Then a × b = h3 − 612 − 99 − 6i = h−333i is a normal vector to the plane, and an equation of the plane is −3( − 0) + 3[ − (−4)] + 3( − 0) = 0 or −3 + 3 + 3 = −12 or − − = 4. 37. Normal vectors for the given planes are n1 = h123i and n2 = h2 −11i. A direction vector, then, for the line of intersection is a = n1 × n2 = h2 + 36 − 1 −1 − 4i = h55 −5i, and a is parallel to the desired plane. Another vector parallel to the plane is the vector connecting any point on the line of intersection to the given point (314) in the plane. Setting = 0, the equations of the planes reduce to + 2 = 1 and 2 − = −3 with simultaneous solution = −1 and = 1. So a point on the line is (−110) and another vector parallel to the plane is b = h3 − (−1)1 − 14 − 0i = h404i. Then a normal vector to the plane is n = a × b = h20 − 0 −20 − 20 0 − 20i = h20 −40 −20i. Equivalently, we can take h1 −2 −1i as a normal vector, and an equation of the plane is 1( − 3) − 2( − 1) − 1( − 4) = 0 or − 2 − = −3. 38. The points (0 −25) and (−131) lie in the desired plane, so the vector v1 = h−15 −4i connecting them is parallel to the plane. The desired plane is perpendicular to the plane 2 = 5 + 4 or 5 + 4 − 2 = 0 and for perpendicular planes, °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.44 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE a normal vector for one plane is parallel to the other plane, so v2 = h54 −2i is also parallel to the desired plane. A normal vector to the desired plane is n = v1 × v2 = h−10 + 16 −20 − 2 −4 − 25i = h6 −22 −29i. Taking (0 0 0) = (0 −2 5), the equation we are looking for is 6( − 0) − 22( + 2) − 29( − 5) = 0 or 6 − 22 − 29 = −101. 39. If a plane is perpendicular to two other planes, its normal vector is perpendicular to the normal vectors of the other two planes. Thus h21 −2i × h1 0 3i = h3 − 0 −2 − 60 − 1i = h3 −8 −1i is a normal vector to the desired plane. The point (151) lies on the plane, so an equation is 3( − 1) − 8( − 5) − ( − 1) = 0 or 3 − 8 − = −38. 40. n1 = h10 −1i and n2 = h012i. Setting = 0, it is easy to see that (130) is a point on the line of intersection of − = 1 and + 2 = 3. The direction of this line is v1 = n1 × n2 = h1 −21i. A second vector parallel to the desired plane is v2 = h1 1 −2i, since it is perpendicular to + − 2 = 1. Therefore, a normal of the plane in question is n = v1 × v2 = h4 − 11 + 2 1 + 2i = h333i, or we can use h111i. Taking (0 0 0) = (1 30), the equation we are looking for is ( − 1) + ( − 3) + = 0 ⇔ + + = 4. 41. To find the -intercept we set = = 0 in the equation 2 + 5 + = 10 and obtain 2 = 10 ⇒ = 5 so the -intercept is (500). When = = 0 we get 5 = 10 ⇒ = 2, so the -intercept is (020). Setting = = 0 gives = 10, so the -intercept is (00 10) and we graph the portion of the plane that lies in the first octant. 42. To find the -intercept we set = = 0 in the equation 3 + + 2 = 6 and obtain 3 = 6 ⇒ = 2 so the -intercept is (200). When = = 0 we get = 6 so the -intercept is (060). Setting = = 0 gives 2 = 6 ⇒ = 3, so the -intercept is (0 03). The figure shows the portion of the plane that lies in the first octant. 43. Setting = = 0 in the equation 6 − 3 + 4 = 6 gives 6 = 6 ⇒ = 1, when = = 0 we have −3 = 6 ⇒ = −2, and = = 0 implies 4 = 6 ⇒ = 3 2 , so the intercepts are (1 0 0), (0 −20), and (00 3 2). The figure shows the portion of the plane cut off by the coordinate planes. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.5 EQUATIONS OF LINES AND PLANES ¤ 45 44. Setting = = 0 in the equation 6 + 5 − 3 = 15 gives 6 = 15 ⇒ = 5 2, when = = 0 we have 5 = 15 ⇒ = 3, and = = 0 implies −3 = 15 ⇒ = −5, so the intercepts are ( 5 2 00), (030), and (00 −5). The figure shows the portion of the plane cut off by the coordinate planes. 45. Substitute the parametric equations of the line into the equation of the plane: + 2 − = 7 ⇒ (2 − 2) + 2(3) − (1 + ) = 7 ⇒ 3 + 1 = 7 ⇒ = 2. Therefore, the point of intersection of the line and the plane is given by = 2 − 2(2) = −2, = 3(2) = 6, and = 1 + 2 = 3, that is, the point (−263). 46. Substitute the parametric equations of the line into the equation of the plane: 3( − 1) − (1 + 2) + 2(3 − ) = 5 ⇒ − + 2 = 5 ⇒ = −3. Therefore, the point of intersection of the line and the plane is given by = −3 − 1 = −4, = 1 + 2(−3) = −5, and = 3 − (−3) = 6, that is, the point (−4 −56). 47. Parametric equations for the line are = 1 5 , = 2, = − 2 and substitution into the equation of the plane gives 10 1 5 − 7(2) + 3( − 2) + 24 = 0 ⇒ −9 + 18 = 0 ⇒ = 2. Thus = 1 5(2) = 2 5, = 2(2) = 4, = 2 − 2 = 0 and the point of intersection is 2 5 4 0. 48. A direction vector for the line through (−310) and (−156) is v = h2 4 6i and, taking 0 = (−3 1 0), parametric equations for the line are = −3 + 2, = 1 + 4, = 6. Substitution of the parametric equations into the equation of the plane gives 2(−3 + 2) + (1 + 4) − (6) = −2 ⇒ 2 − 5 = −2 ⇒ = 3 2. Then = −3 + 2 3 2 = 0, = 1 + 4 3 2 = 7, and = 6 3 2 = 9, and the point of intersection is (0 7 9). 49. Setting = 0, we see that (0 1 0) satisfies the equations of both planes, so that they do in fact have a line of intersection. v = n1 × n2 = h111i × h101i = h10 −1i is the direction of this line. Therefore, direction numbers of the intersecting line are 1, 0, −1. 50. The angle between the two planes is the same as the angle between their normal vectors. The normal vectors of the two planes are h111i and h123i. The cosine of the angle between these two planes is cos = h1 1 1i · h123i |h1 1 1i| |h123i| = 1 + 2 + 3 √1 + 1 + 1√1 + 4 + 9 = 6 √42 = 6 7. 51. Normal vectors for the planes are n1 = h14 −3i and n2 = h−367i. The normals aren’t parallel (they are not scalar multiples of each other), so neither are the planes. But n1 · n2 = −3 + 24 − 21 = 0, so the normals, and thus the planes, are perpendicular. 52. Normal vectors for the planes are n1 = h9 −3 6i and n2 = h6 −24i (the plane’s equation is 6 − 2 + 4 = 0). Since n1 = 3 2n2, the normals, and thus the planes, are parallel. 53. Normal vectors for the planes are n1 = h12 −1i and n2 = h2 −21i. The normals are not parallel (they are not scalar multiples of each other), so neither are the planes. Furthermore, n1 · n2 = 2 − 4 − 1 = −3 6= 0, so the planes aren’t °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.46 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE perpendicular. The angle between the planes is the same as the angle between the normals, given by cos = n1 · n2 |n1| |n2| = −3 √6√9 = − 1 √ 6 ⇒ = cos−1−√16 ≈ 1141◦. 54. Normal vectors for the planes are n1 = h1 −13i and n2 = h3 1 −1i. The normals are not parallel, so neither are the planes. Since n1 · n2 = 3 − 1 − 3 = −1 6= 0, the planes aren’t perpendicular. The angle between the planes is given by cos = n1 · n2 |n1| |n2| = −1 √11√11 = − 1 11 ⇒ = cos−1− 11 1 ≈ 952◦. 55. The planes are 2 − 3 − = 0 and 4 − 6 − 2 = 3 with normal vectors n1 = h2 −3 −1i and n2 = h4 −6 −2i. Since n2 = 2n1, the normals, and thus the planes, are parallel. 56. The normals are n1 = h52 3i and n2 = h4 −1 −6i which are not scalar multiples of each other, so the planes aren’t parallel. Since n1 · n2 = 20 − 2 − 18 = 0, the normals, and thus the planes, are perpendicular. 57. (a) To find a point on the line of intersection, set one of the variables equal to a constant, say = 0. (This will fail if the line of intersection does not cross the -plane; in that case, try setting or equal to 0.) The equations of the two planes reduce to + = 1 and + 2 = 1. Solving these two equations gives = 1, = 0. Thus a point on the line is (100). A vector v in the direction of this intersecting line is perpendicular to the normal vectors of both planes, so we can take v = n1 × n2 = h1 1 1i × h122i = h2 − 21 − 22 − 1i = h0 −1 1i. By Equations 2, parametric equations for the line are = 1, = −, = . (b) The angle between the planes satisfies cos = n1 · n2 |n1| |n2| = 1 + 2 + 2 √3√9 = 5 3√3. Therefore = cos−13√5 3 ≈ 158◦. 58. (a) If we set = 0 then the equations of the planes reduce to 3 − 2 = 1 and 2 + = 3 and solving these two equations gives = 1, = 1. Thus a point on the line of intersection is (110). A vector v in the direction of this intersecting line is perpendicular to the normal vectors of both planes, so let v = n1 × n2 = h3 −2 1i × h2 1 −3i = h5117i. By Equations 2, parametric equations for the line are = 1 + 5, = 1 + 11, = 7. (b) cos = n1 · n2 |n1| |n2| = 6 − 2 − 3 √14√14 = 1 14 ⇒ = cos−1 14 1 ≈ 859◦. 59. Setting = 0, the equations of the two planes become 5 − 2 = 1 and 4 + = 6. Solving these two equations gives = 1, = 2 so a point on the line of intersection is (120). A vector v in the direction of this intersecting line is perpendicular to the normal vectors of both planes. So we can use v = n1 × n2 = h5 −2 −2i × h411i = h0 −1313i or equivalently we can take v = h0 −11i, and symmetric equations for the line are = 1, − 2 −1 = 1 or = 1, − 2 = −. 60. If we set = 0 then the equations of the planes reduce to 2 − − 5 = 0 and 4 + 3 − 5 = 0 and solving these two equations gives = 2, = −1. Thus a point on the line of intersection is (2 −10). A vector v in the direction of this intersecting line is perpendicular to the normal vectors of both planes, so take v = n1 ×n2 = h2 −1 −1i × h43 −1i = h4 −210i or equivalently we can take v = h2 −15i. Symmetric equations for the line are − 2 2 = + 1 −1 = 5 . °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.5 EQUATIONS OF LINES AND PLANES ¤ 47 61. The distance from a point ( ) to (10 −2) is 1 = ( − 1)2 + 2 + ( + 2)2 and the distance from ( ) to (340) is 2 = ( − 3)2 + ( − 4)2 + 2. The plane consists of all points ( ) where 1 = 2 ⇒ 12 = 22 ⇔ ( − 1)2 + 2 + ( + 2)2 = ( − 3)2 + ( − 4)2 + 2 ⇔ 2 − 2 + 2 + 2 + 4 + 5 = 2 − 6 + 2 − 8 + 2 + 25 ⇔ 4 + 8 + 4 = 20 so an equation for the plane is 4 + 8 + 4 = 20 or equivalently + 2 + = 5. Alternatively, you can argue that the segment joining points (10 −2) and (3 4 0) is perpendicular to the plane and the plane includes the midpoint of the segment. 62. The distance from a point ( ) to (255) is 1 = ( − 2)2 + ( − 5)2 + ( − 5)2 and the distance from ( ) to (−631) is 2 = ( + 6)2 + ( − 3)2 + ( − 1)2. The plane consists of all points ( ) where 1 = 2 ⇒ 12 = 22 ⇔ ( − 2)2 + ( − 5)2 + ( − 5)2 = ( + 6)2 + ( − 3)2 + ( − 1)2 ⇔ 2 − 4 + 2 − 10 + 2 − 10 + 54 = 2 + 12 + 2 − 6 + 2 − 2 + 46 ⇔ 16 + 4 + 8 = 8 so an equation for the plane is 16 + 4 + 8 = 8 or equivalently 4 + + 2 = 2. 63. The plane contains the points (00), (0 0) and (00 ). Thus the vectors a = h− 0i and b = h− 0 i lie in the plane, and n = a × b = h − 00 + 0 + i = h i is a normal vector to the plane. The equation of the plane is therefore + + = + 0 + 0 or + + = . Notice that if 6= 0, 6= 0 and 6= 0 then we can rewrite the equation as + + = 1. This is a good equation to remember! 64. (a) For the lines to intersect, we must be able to find one value of and one value of satisfying the three equations 1 + = 2 − , 1 − = and 2 = 2. From the third we get = 1, and putting this in the second gives = 0. These values of and do satisfy the first equation, so the lines intersect at the point 0 = (1 + 11 − 1 2(1)) = (202). (b) The direction vectors of the lines are h1 −12i and h−1 1 0i, so a normal vector for the plane is h−11 0i × h1 −12i = h220i and it contains the point (202). Then an equation of the plane is 2( − 2) + 2( − 0) + 0( − 2) = 0 ⇔ + = 2. 65. Two vectors which are perpendicular to the required line are the normal of the given plane, h1 1 1i, and a direction vector for the given line, h1 −12i. So a direction vector for the required line is h111i × h1 −12i = h3 −1 −2i. Thus is given by h i = h012i + h3 −1 −2i, or in parametric form, = 3, = 1 − , = 2 − 2. 66. Let be the given line. Then (110) is the point on corresponding to = 0. is in the direction of a = h1 −12i and b = h−102i is the vector joining (110) and (0 1 2). Then b − proja b = h−102i − h1 −12i · h−1 0 2i 12 + (−1)2 + 22 h1 −12i = h−1 0 2i − 1 2h1 −12i = − 3 2 1 21 is a direction vector for the required line. Thus 2− 3 2 1 2 1 = h−312i is also a direction vector, and the line has parametric equations = −3, = 1 + , = 2 + 2. (Notice that this is the same line as in Exercise 65.) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.48 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 67. Let have normal vector n. Then n1 = h36 −3i, n2 = h4 −128i, n3 = h3 −9 6i, n4 = h1 2 −1i. Now n1 = 3n4, so n1 and n4 are parallel, and hence 1 and 4 are parallel; similarly 2 and 3 are parallel because n2 = 4 3n3. However, n1 and n2 are not parallel (so not all four planes are parallel). Notice that the point (200) lies on both 1 and 4, so these two planes are identical. The point 5 4 00 lies on 2 but not on 3, so these are different planes. 68. Let have direction vector v. Rewrite the symmetric equations for 3 as − 1 12 = − 1 −14 = + 1 1 ; then v1 = h6 −312i, v2 = h214i, v3 = 1 2 − 1 4 1, and v4 = h428i. v1 = 12v3, so 1 and 3 are parallel. v4 = 2v2, so 2 and 4 are parallel. (Note that 1 and 2 are not parallel.) 1 contains the point (115), but this point does not lie on 3, so they’re not identical. (315) lies on 4 and also on 2 (for = 1), so 2 and 4 are the same line. 69. Let = (1 34) and = (211), points on the line corresponding to = 0 and = 1. Let = (4 1 −2). Then a = −→ = h1 −2 −3i, b = −−→ = h3 −2 −6i. The distance is = |a × b| |a| = |h1 −2 −3i × h3 −2 −6i| |h1 −2 −3i| = |h6 −34i| |h1 −2 −3i| = 62 + (−3)2 + 42 12 + (−2)2 + (−3)2 = √61 √14 = 61 14. 70. Let = (0 63) and = (244), points on the line corresponding to = 0 and = 1. Let = (0 1 3). Then a = −→ = h2 −21i and b = −−→ = h0 −50i. The distance is = |a × b| |a| = |h2 −21i × h0 −50i| |h2 −21i| = |h50 −10i| |h2 −21i| = 52 + 02 + (−10)2 22 + (−2)2 + 12 = √125 √9 = 5√5 3 . 71. By Equation 9, the distance is = |1√+2+1 +2 +12+ | = |3(1) + 2( √32−+ 2 2) + 6(4) 2 + 62 − 5| = √|18 49| = 18 7 . 72. By Equation 9, the distance is = |1( −16) 2 + ( − 2(3) −2)2−+ ( 4(5) −4) −28| = |√−40 21| = √40 21. 73. Put = = 0 in the equation of the first plane to get the point (200) on the plane. Because the planes are parallel, the distance between them is the distance from (200) to the second plane. By Equation 9, = |4(2) 42−+ ( 6(0) + 2(0) −6)2 + (2) −23| = √556 = 2√514 or 5√2814. 74. Put = = 0 in the equation of the first plane to get the point (000) on the plane. Because the planes are parallel the distance between them is the distance from (000) to the second plane 3 − 6 + 9 − 1 = 0. By Equation 9, = |3(0) 3−2 6(0) + 9(0) + (−6)2 + 9−2 1| = √126 1 = 3√114. 75. The distance between two parallel planes is the same as the distance between a point on one of the planes and the other plane. Let 0 = (0 0 0) be a point on the plane given by + + + 1 = 0. Then 0 + 0 + 0 + 1 = 0 and the °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.5 EQUATIONS OF LINES AND PLANES ¤ 49 distance between 0 and the plane given by + + + 2 = 0 is, from Equation 9, = |0√+ 2 +0 +2 +0+2 2| = √|−2+1 +2 +2|2 = √|21+−22 +| 2 . 76. The planes must have parallel normal vectors, so if + + + = 0 is such a plane, then for some 6= 0, h i = h12 −2i = h2 −2i. So this plane is given by the equation + 2 − 2 + = 0, where = . By Exercise 75, the distance between the planes is 2 = 12 + 2 |1 −2 + ( | −2)2 ⇔ 6 = |1 − | ⇔ = 7 or −5. So the desired planes have equations + 2 − 2 = 7 and + 2 − 2 = −5. 77. 1: = = ⇒ = (1). 2: + 1 = 2 = 3 ⇒ + 1 = 2 (2). The solution of (1) and (2) is = = −2. However, when = −2, = ⇒ = −2, but + 1 = 3 ⇒ = −3, a contradiction. Hence the lines do not intersect. For 1, v1 = h111i, and for 2, v2 = h1 2 3i, so the lines are not parallel. Thus the lines are skew lines. If two lines are skew, they can be viewed as lying in two parallel planes and so the distance between the skew lines would be the same as the distance between these parallel planes. The common normal vector to the planes must be perpendicular to both h1 1 1i and h123i, the direction vectors of the two lines. So set n = h111i × h123i = h3 − 2 −3 + 1 2 − 1i = h1 −21i. From above, we know that (−2 −2 −2) and (−2 −2 −3) are points of 1 and 2 respectively. So in the notation of Equation 8, 1(−2) − 2(−2) + 1(−2) + 1 = 0 ⇒ 1 = 0 and 1(−2) − 2(−2) + 1(−3) + 2 = 0 ⇒ 2 = 1. By Exercise 75, the distance between these two skew lines is = √1 + 4 + 1 |0 − 1| = √16. Alternate solution (without reference to planes): A vector which is perpendicular to both of the lines is n = h111i × h123i = h1 −21i. Pick any point on each of the lines, say (−2 −2 −2) and (−2 −2 −3), and form the vector b = h001i connecting the two points. The distance between the two skew lines is the absolute value of the scalar projection of b along n, that is, = |n · b| |n| = |1 · 0 − 2 · 0 + 1 · 1| √1 + 4 + 1 = 1 √ 6 . 78. First notice that if two lines are skew, they can be viewed as lying in two parallel planes and so the distance between the skew lines would be the same as the distance between these parallel planes. The common normal vector to the planes must be perpendicular to both v1 = h16 2i and v2 = h2156i, the direction vectors of the two lines respectively. Thus set n = v1 × v2 = h36 − 30 4 − 615 − 12i = h6 −23i. Setting = 0 and = 0 gives the points (110) and (15 −2). So in the notation of Equation 8, 6 − 2 + 0 + 1 = 0 ⇒ 1 = −4 and 6 − 10 − 6 + 2 = 0 ⇒ 2 = 10. Then by Exercise 75, the distance between the two skew lines is given by = √|36 + 4 + 9 −4 − 10| = 14 7 = 2. Alternate solution (without reference to planes): We already know that the direction vectors of the two lines are v1 = h162i and v2 = h2156i. Then n = v1 × v2 = h6 −2 3i is perpendicular to both lines. Pick any point on each of the lines, say (110) and (15 −2), and form the vector b = h04 −2i connecting the two points. Then the distance between the two skew lines is the absolute value of the scalar projection of b along n, that is, = |n · b| |n| = 1 √36 + 4 + 9 |0 − 8 − 6| = 14 7 = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.50 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 79. A direction vector for 1 is v1 = h20 −1i and a direction vector for 2 is v2 = h322i. These vectors are not parallel so neither are the lines. Parametric equations for the lines are 1: = 2, = 0, = −, and 2: = 1 + 3, = −1 + 2, = 1 + 2. No values of and satisfy these equations simultaneously, so the lines don’t intersect and hence are skew. We can view the lines as lying in two parallel planes; a common normal vector to the planes is n = v1 × v2 = h2 −74i. Line 1 passes through the origin, so (000) lies on one of the planes, and (1 −1 1) is a point on 2 and therefore on the other plane. Equations of the planes then are 2 − 7 + 4 = 0 and 2 − 7 + 4 − 13 = 0, and by Exercise 75, the distance between the two skew lines is = √|04 + 49 + 16 − (−13)| = √13 69. Alternate solution (without reference to planes): Direction vectors of the two lines are v1 = h20 −1i and v2 = h32 2i. Then n = v1 ×v2 = h2 −74i is perpendicular to both lines. Pick any point on each of the lines, say (000) and (1 −11), and form the vector b = h1 −11i connecting the two points. Then the distance between the two skew lines is the absolute value of the scalar projection of b along n, that is, = |n · b| |n| = |2 + 7 + 4| √4 + 49 + 16 = 13 √69. 80. A direction vector for the line 1 is v1 = h122i. A normal vector for the plane 1 is n1 = h1 −12i. The vector from the point (0 0 1) to (32 −1), h32 −2i, is parallel to the plane 2, as is the vector from (001) to (121), namely h1 2 0i. Thus a normal vector for 2 is h32 −2i × h120i = h4 −24i, or we can use n2 = h2 −12i, and a direction vector for the line 2 of intersection of these planes is v2 = n1 × n2 = h1 −12i × h2 −12i = h0 2 1i. Notice that the point (32 −1) lies on both planes, so it also lies on 2. The lines are skew, so we can view them as lying in two parallel planes; a common normal vector to the planes is n = v1 × v2 = h−2 −12i. Line 1 passes through the point (126), so (126) lies on one of the planes, and (32 −1) is a point on 2 and therefore on the other plane. Equations of the planes then are −2 − + 2 − 8 = 0 and −2 − + 2 + 10 = 0, and by Exercise 75, the distance between the lines is = √|−4 + 1 + 4 8 − 10| = 18 3 = 6. Alternatively, direction vectors for the lines are v1 = h1 2 2i and v2 = h02 1i, so n = v1 × v2 = h−2 −1 2i is perpendicular to both lines. Pick any point on each of the lines, say (1 2 6) and (32 −1), and form the vector b = h2 0 −7i connecting the two points. Then the distance between the two skew lines is the absolute value of the scalar projection of b along n, that is, = |n · b| |n| = |−4 + 0 − 14| √4 + 1 + 4 = 18 3 = 6. 81. (a) A direction vector from tank A to tank B is h765 − 325 675 − 810599 − 561i = h440 −13538i. Taking tank A’s position (325810561) as the initial point, parametric equations for the line of sight are = 325 + 440, = 810 − 135, = 561 + 38 for 0 ≤ ≤ 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.LABORATORY PROJECT PUTTING 3D IN PERSPECTIVE ¤ 51 (b) We divide the line of sight into 5 equal segments, corresponding to ∆ = 02, and compute the elevation from the -component of the parametric equations in part (a): = 561 + 38 terrain elevation 0 5610 02 5686 549 04 5762 566 06 5838 586 08 5914 589 10 5990 Since the terrain is higher than the line of sight when = 06, the tanks can’t see each other. 82. (a) The planes + + = have normal vector h1 1 1i, so they are all parallel. Their -, -, and -intercepts are all . When 0 their intersection with the first octant is an equilateral triangle and when 0 their intersection with the octant diagonally opposite the first is an equilateral triangle. (b) The planes + + = 1 have -intercept 1, -intercept 1, and -intercept 1. The plane with = 0 is parallel to the -axis. As gets larger, the planes get closer to the -plane. (c) The planes cos + cos = 1 have normal vectors h0cos sini, which are perpendicular to the -axis, and so the planes are parallel to the -axis. We look at their intersection with the -plane. These are lines that are perpendicular to hcos sini and pass through (cossin), since cos2 + sin2 = 1. So these are the tangent lines to the unit circle. Thus the family consists of all planes tangent to the circular cylinder with radius 1 and axis the -axis. 83. If 6= 0, then + + + = 0 ⇒ ( + ) + ( − 0) + ( − 0) = 0 which by (7) is the scalar equation of the plane through the point (−00) with normal vector h i. Similarly, if 6= 0 (or if 6= 0) the equation of the plane can be rewritten as ( − 0) + ( + ) + ( − 0) = 0 [or as ( − 0) + ( − 0) + ( + ) = 0] which by (7) is the scalar equation of a plane through the point (0 −0) [or the point (00 −)] with normal vector h i. LABORATORY PROJECT Putting 3D in Perspective 1. If we view the screen from the camera’s location, the vertical clipping plane on the left passes through the points (100000), (0 −4000), and (0 −400 600). A vector from the first point to the second is v1 = h−1000 −400 0i and a vector from the first point to the third is v2 = h−1000 −400600i. A normal vector for the clipping plane is v1 × v2 = −240,000i + 600,000j or −2i + 5j, and an equation for the plane is −2( − 1000) + 5( − 0) + 0( − 0) = 0 ⇒ 2 − 5 = 2000. By symmetry, the vertical clipping plane on the right is given by 2 + 5 = 2000. The lower clipping plane is = 0. The upper clipping plane passes through the points (100000), °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.52 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE (0 −400600), and (0400600). Vectors from the first point to the second and third points are v1 = h−1000 −400600i and v2 = h−1000400 600i, and a normal vector for the plane is v1 × v2 = −480,000i − 800,000k or 3i + 5k. An equation for the plane is 3( − 1000) + 0( − 0) + 5( − 0) = 0 ⇒ 3 + 5 = 3000. A direction vector for the line is v = h630 390162i and taking 0 = (230 −285102), parametric equations are = 230 + 630, = −285 + 390, = 102 + 162. intersects the left clipping plane when 2(230 + 630) − 5(−285 + 390) = 2000 ⇒ = − 1 6 . The corresponding point is (125 −35075). intersects the right clipping plane when 2(230 + 630) + 5(−285 + 390) = 2000 ⇒ = 593 642 . The corresponding point is approximately (8119 7522516), but this point is not contained within the viewing volume. intersects the upper clipping plane when 3(230 + 630) + 5(102 + 162) = 3000 ⇒ = 2 3 , corresponding to the point (650 −25 210), and intersects the lower clipping plane when = 0 ⇒ 102 + 162 = 0 ⇒ = − 17 27 . The corresponding point is approximately (−1667 −53060), which is not contained within the viewing volume. Thus should be clipped at the points (125 −35075) and (650 −25210). 2. A sight line from the camera at (1000 0 0) to the left endpoint (125 −35075) of the clipped line has direction v = h−875 −350 75i. Parametric equations are = 1000 − 875, = −350, = 75. This line intersects the screen when = 0 ⇒ 1000 − 875 = 0 ⇒ = 8 7 , corresponding to the point 0 −400 600 7 . Similarly, a sight line from the camera to the right endpoint (650 −25 210) of the clipped line has direction h−350 −25210i and parametric equations are = 1000 − 350, = −25, = 210. = 0 ⇒ 1000 − 350 = 0 ⇒ = 20 7 , corresponding to the point 0 − 500 7 600. Thus the projection of the clipped line is the line segment between the points 0 −400 600 7 and 0 − 500 7 600. 3. From Equation 12.5.4, equations for the four sides of the screen are r1() = (1 − )h0 −4000i + h0 −400600i, r2() = (1 − )h0 −400600i + h0400 600i, r3() = (1 − )h04000i + h0400 600i, and r4() = (1 − )h0 −4000i + h04000i. The clipped line segment connects the points (125 −350 75) and (650 −25 210), so an equation for the segment is r5() = (1 − )h125 −35075i + h650 −25 210i. The projection of the clipped segment connects the points 0 −400 600 7 and 0 − 500 7 600, so an equation is r6() = (1 − )0 −400 600 7 + 0 − 500 7 600. The sight line on the left connects the points (100000) and 0 −400 600 7 , so an equation is r7() = (1 − )h100000i + 0 −400 600 7 . The other sight line connects (100000) to 0 − 500 7 600, so an equation is r8() = (1 − )h1000 0 0i + 0 − 500 7 600. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.6 CYLINDERS AND QUADRIC SURFACES ¤ 53 4. The vector from (621 −147 206) to (56331242), v1 = h−5817836i, lies in the plane of the rectangle, as does the vector from (621 −147206) to (657 −111 86), v2 = h3636 −120i. A normal vector for the plane is v1 × v2 = h−1888 −142 −708i or h823i, and an equation of the plane is 8 + 2 + 3 = 5292. The line intersects this plane when 8(230 + 630) + 2(−285 + 390) + 3(102 + 162) = 5292 ⇒ = 1858 3153 ≈ 0589. The corresponding point is approximately (60125 −5518 19746). Starting at this point, a portion of the line is hidden behind the rectangle. The line becomes visible again at the left edge of the rectangle, specifically the edge between the points (621 −147206) and (657 −111 86). (This is most easily determined by graphing the rectangle and the line.) A plane through these two points and the camera’s location, (100000), will clip the line at the point it becomes visible. Two vectors in this plane are v1 = h−379 −147206i and v2 = h−343 −11186i. A normal vector for the plane is v1 ×v2 = h10224 −38064 −8352i and an equation of the plane is 213 − 793 − 174 = 213,000. intersects this plane when 213(230 + 630) − 793(−285 + 390) − 174(102 + 162) = 213,000 ⇒ = 203 44,247 ,268 ≈ 02177. The corresponding point is approximately (36714 −2001113726). Thus the portion of that should be removed is the segment between the points (60125 −551819746) and (36714 −2001113726). 12.6 Cylinders and Quadric Surfaces 1. (a) In R2, the equation = 2 represents a parabola. (b) In R3, the equation = 2 doesn’t involve , so any horizontal plane with equation = intersects the graph in a curve with equation = 2. Thus, the surface is a parabolic cylinder, made up of infinitely many shifted copies of the same parabola. The rulings are parallel to the -axis. (c) In R3, the equation = 2 also represents a parabolic cylinder. Since doesn’t appear, the graph is formed by moving the parabola = 2 in the direction of the -axis. Thus, the rulings of the cylinder are parallel to the -axis. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.54 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 2. (a) (b) Since the equation = doesn’t involve , horizontal traces are copies of the curve = . The rulings are parallel to the -axis. (c) The equation = doesn’t involve , so vertical traces in = (parallel to the -plane) are copies of the curve = . The rulings are parallel to the -axis. 3. Since is missing from the equation, the vertical traces 2 + 2 = 1, = , are copies of the same circle in the plane = . Thus the surface 2 + 2 = 1 is a circular cylinder with rulings parallel to the -axis. 4. Since is missing from the equation, the horizontal traces 42 + 2 = 4, = , are copies of the same ellipse in the plane = . Thus the surface 42 + 2 = 4 is an elliptic cylinder with rulings parallel to the -axis. 5. Since is missing, each vertical trace = 1 − 2, = , is a copy of the same parabola in the plane = . Thus the surface = 1 − 2 is a parabolic cylinder with rulings parallel to the -axis. . 6. Since is missing, each vertical trace = 2, = , is a copy of the same parabola in the plane = . Thus the surface = 2 is a parabolic cylinder with rulings parallel to the -axis. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.6 CYLINDERS AND QUADRIC SURFACES ¤ 55 7. Since is missing, each horizontal trace = 1, = , is a copy of the same hyperbola in the plane = . Thus the surface = 1 is a hyperbolic cylinder with rulings parallel to the -axis. 8. Since is missing, each vertical trace = sin, = , is a copy of a sine curve in the plane = . Thus the surface = sin is a cylindrical surface with rulings parallel to the -axis. 9. (a) The traces of 2 + 2 − 2 = 1 in = are 2 − 2 = 1 − 2, a family of hyperbolas. (Note that the hyperbolas are oriented differently for −1 1 than for −1 or 1.) The traces in = are 2 − 2 = 1 − 2, a similar family of hyperbolas. The traces in = are 2 + 2 = 1 + 2, a family of circles. For = 0, the trace in the -plane, the circle is of radius 1. As || increases, so does the radius of the circle. This behavior, combined with the hyperbolic vertical traces, gives the graph of the hyperboloid of one sheet in Table 1. (b) The shape of the surface is unchanged, but the hyperboloid is rotated so that its axis is the -axis. Traces in = are circles, while traces in = and = are hyperbolas. (c) Completing the square in gives 2 + ( + 1)2 − 2 = 1. The surface is a hyperboloid identical to the one in part (a) but shifted one unit in the negative -direction. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.56 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 10. (a) The traces of −2 − 2 + 2 = 1 in = are −2 + 2 = 1 + 2, a family of hyperbolas, as are the traces in = , −2 + 2 = 1 + 2. The traces in = are 2 + 2 = 2 − 1, a family of circles for || 1. As || increases, the radii of the circles increase; the traces are empty for || 1. This behavior, combined with the vertical traces, gives the graph of the hyperboloid of two sheets in Table 1. (b) The graph has the same shape as the hyperboloid in part (a) but is rotated so that its axis is the -axis. Traces in = , || 1, are circles, while traces in = and = are hyperbolas. 11. For = 2 + 42, the traces in = are 2 + 42 = . When 0 we have a family of ellipses. When = 0 we have just a point at the origin, and the trace is empty for 0. The traces in = are = 42 + 2, a family of parabolas opening in the positive -direction. Similarly, the traces in = are = 2 + 42, a family of parabolas opening in the positive -direction. We recognize the graph as an elliptic paraboloid with axis the -axis and vertex the origin. 12. 42 + 92 + 92 = 36. The traces in = are 92 + 92 = 36 − 42 ⇔ 2 + 2 = 4 − 4 92, a family of circles for || 3. (The traces are a single point for || = 3 and are empty for || 3.) The traces in = are 42 + 92 = 36 − 92, a family of ellipses for || 2. Similarly, the traces in = are the ellipses 42 + 92 = 36 − 92, || 2. The graph is an ellipsoid centered at the origin with intercepts = ±3, = ±2, = ±2. 13. 2 = 42 + 2. The traces in = are the ellipses 42 + 2 = 2. The traces in = are 2 − 2 = 42, hyperbolas for 6= 0 and two intersecting lines if = 0. Similarly, the traces in = are 2 − 42 = 2, hyperbolas for 6= 0 and two intersecting lines if = 0. We recognize the graph as an elliptic cone with axis the -axis and vertex the origin. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.6 CYLINDERS AND QUADRIC SURFACES ¤ 57 14. 2 − 42 − 2 = 4. The traces in = are the hyperbolas 2 − 2 = 4 + 42, and the traces in = are the hyperbolas 2 − 42 = 4 + 2. The traces in = are 42 + 2 = 2 − 4, a family of ellipses for || 2. (The traces are a single point for || = 2 and are empty for || 2.) The surface is a hyperboloid of two sheets with axis the -axis. 15. 92 + 42 = 2 + 36. The traces in = are 92 + 42 = 2 + 36, a family of ellipses. The traces in = are 42 − 2 = 9(4 − 2), a family of hyperbolas for || 6= 2 and two intersecting lines when || = 2. (Note that the hyperbolas are oriented differently for || 2 than for || 2.) The traces in = are 92 − 2 = 4(9 − 2), a family of hyperbolas when || 6= 3 (oriented differently for || 3 than for || 3) and two intersecting lines when || = 3. We recognize the graph as a hyperboloid of one sheet with axis the -axis. 16. 32 + + 32 = 0. The traces in = are the parabolas = −32 − 32 which open to the left (in the negative -direction). Traces in = are 32 + 32 = − ⇔ 2 + 2 = − 3 , a family of circles for 0. (Traces are empty for 0 and a single point for = 0.) Traces in = are the parabolas = −32 − 32 which open in the negative -direction. The graph is a circular paraboloid with axis the -axis, opening in the negative -direction, and vertex the origin. 17. 2 9 + 2 25 + 2 4 = 1. The traces in = are 25 2 + 42 = 1 − 92 , a family of ellipses for || 3. (The traces are a single point for || = 3 and are empty for || 3.) The traces in = are the ellipses 2 9 + 2 4 = 1 − 25 2 , || 5, and the traces in = are the ellipses 2 9 + 2 25 = 1 − 2 4 , || 2. The surface is an ellipsoid centered at the origin with intercepts = ±3, = ±5, = ±2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.58 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 18. 32 − 2 + 32 = 0. The traces in = are 2 − 32 = 32, a family of hyperbolas for 6= 0 and two intersecting lines if = 0. Traces in = are the circles 32 + 32 = 2 ⇔ 2 + 2 = 1 32. The traces in = are 2 − 32 = 32, hyperbolas for 6= 0 and two intersecting lines if = 0. We recognize the surface as a circular cone with axis the -axis and vertex the origin. 19. = 2 − 2. The traces in = are the parabolas = 2 − 2, opening in the positive -direction. The traces in = are = 2 − 2, two intersecting lines when = 0 and a family of hyperbolas for 6= 0 (note that the hyperbolas are oriented differently for 0 than for 0). The traces in = are the parabolas = 2 − 2 which open in the negative -direction. Thus the surface is a hyperbolic paraboloid centered at (000). 20. = 2 − 2. The traces in = are 2 − 2 = , two intersecting lines when = 0 and a family of hyperbolas for 6= 0 (oriented differently for 0 than for 0). The traces in = are the parabolas = −2 + 2, opening in the negative -direction, and the traces in = are the parabolas = 2 − 2 which open in the positive -direction. The graph is a hyperbolic paraboloid centered at (000). 21. This is the equation of an ellipsoid: 2 + 42 + 92 = 2 + 2 (12)2 + 2 (13)2 = 1, with -intercepts ±1, -intercepts ± 1 2 and -intercepts ± 1 3 . So the major axis is the -axis and the only possible graph is VII. 22. This is the equation of an ellipsoid: 92 + 42 + 2 = 2 (13)2 + 2 (12)2 + 2 = 1, with -intercepts ± 1 3 , -intercepts ± 1 2 and -intercepts ±1. So the major axis is the -axis and the only possible graph is IV. 23. This is the equation of a hyperboloid of one sheet, with = = = 1. Since the coefficient of 2 is negative, the axis of the hyperboloid is the -axis, hence the correct graph is II. 24. This is a hyperboloid of two sheets, with = = = 1. This surface does not intersect the -plane at all, so the axis of the hyperboloid is the -axis and the graph is III. 25. There are no real values of and that satisfy this equation for 0, so this surface does not extend to the left of the -plane. The surface intersects the plane = 0 in an ellipse. Notice that occurs to the first power whereas and occur to the second power. So the surface is an elliptic paraboloid with axis the -axis. Its graph is VI. 26. This is the equation of a cone with axis the -axis, so the graph is I. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.6 CYLINDERS AND QUADRIC SURFACES ¤ 59 27. This surface is a cylinder because the variable is missing from the equation. The intersection of the surface and the -plane is an ellipse. So the graph is VIII. 28. This is the equation of a hyperbolic paraboloid. The trace in the -plane is the parabola = 2. So the correct graph is V. 29. Vertical traces parallel to the -plane are circles centered at the origin whose radii increase as decreases. (The trace in = 1 is just a single point and the graph suggests that traces in = are empty for 1.) The traces in vertical planes parallel to the -plane are parabolas opening to the left that shift to the left as || increases. One surface that fits this description is a circular paraboloid, opening to the left, with vertex (010). 30. The vertical traces parallel to the -plane are ellipses that are smallest in the -plane and increase in size as || increases. One surface that fits this description is a hyperboloid of one sheet with axis the -axis. The horizontal traces in = (hyperbolas and intersecting lines) also fit this surface, as shown in the figure. 31. 2 = 2 + 1 9 2 or 2 = 2 + 2 9 represents an elliptic cone with vertex (0 00) and axis the -axis. 32. 42 − + 22 = 0 or = 2 14 + 2 12 or 4 = 2 + 2 2 represents an elliptic paraboloid with vertex (000) and axis the -axis. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.60 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 33. 2 + 2 − 22 = 0 or 2 = 22 − 2 or = 2 − 2 2 represents a hyperbolic paraboloid with center (0 0 0). 34. 2 = 2 + 42 + 4 or −2 + 2 − 42 = 4 or − 2 4 + 2 4 − 2 = 1 represents a hyperboloid of two sheets with axis the -axis. 35. Completing squares in and gives 2 − 2 + 1 + 2 − 6 + 9 − = 0 ⇔ ( − 1)2 + ( − 3)2 − = 0 or = ( − 1)2 + ( − 3)2, a circular paraboloid opening upward with vertex (1 3 0) and axis the vertical line = 1, = 3. 36. Completing squares in and gives 2 − 4 + 4 − 2 − 2 + 2 + 1 + 3 = 0 + 4 − 1 ⇔ ( − 2)2 − 2 − ( + 1)2 = 0 or ( − 2)2 = 2 + ( + 1)2, a circular cone with vertex (2 0 −1) and axis the horizontal line = 0, = −1. 37. Completing squares in and gives 2 − 4 + 4 − 2 + 2 − 2 + 1 = 0 + 4 + 1 ⇔ ( − 2)2 − 2 + ( − 1)2 = 5 or ( − 2)2 5 − 2 5 + ( − 1)2 5 = 1, a hyperboloid of one sheet with center (2 0 1) and axis the horizontal line = 2, = 1. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.6 CYLINDERS AND QUADRIC SURFACES ¤ 61 38. Completing squares in all three variables gives 4(2 − 6 + 9) + (2 − 8 + 16) + (2 + 4 + 4) = −55 + 36 + 16 + 4 ⇔ 4( − 3)2 + ( − 4)2 + ( + 2)2 = 1 or ( − 3)2 14 + ( − 4)2 + ( + 2)2 = 1, an ellipsoid with center (34 −2). 39. Solving the equation for we get = ±1 + 42 + 2, so we plot separately = 1 + 42 + 2 and = −1 + 42 + 2. To restrict the -range as in the second graph, we can use the option view = -4..4 in Maple’s plot3d command, or PlotRange - {-4,4} in Mathematica’s Plot3D command. 40. We plot the surface = 2 − 2. 41. Solving the equation for we get = ±42 + 2, so we plot separately = 42 + 2 and = −42 + 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.62 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 42. We plot the surface = 2 − 6 + 42. 43. 44. 45. The curve = √ is equivalent to = 2, ≥ 0. Rotating the curve about the -axis creates a circular paraboloid with vertex at the origin, axis the -axis, opening in the positive -direction. The trace in the -plane is = 2, = 0, and the trace in the -plane is a parabola of the same shape: = 2, = 0. An equation for the surface is = 2 + 2. 46. Rotating the line = 2 about the -axis creates a (right) circular cone with vertex at the origin and axis the -axis. Traces in = ( 6= 0) are circles with center (00 ) and radius = 2 = 2, so an equation for the trace is 2 + 2 = (2)2, = . Thus an equation for the surface is 2 + 2 = (2)2 or 42 + 42 = 2. 47. Let = (, , ) be an arbitrary point equidistant from (−1, 0, 0) and the plane = 1. Then the distance from to (−1, 0, 0) is ( + 1)2 + 2 + 2 and the distance from to the plane = 1 is | − 1|√12 = | − 1| (by Equation 12.5.9). So | − 1| = ( + 1)2 + 2 + 2 ⇔ ( − 1)2 = ( + 1)2 + 2 + 2 ⇔ 2 − 2 + 1 = 2 + 2 + 1 + 2 + 2 ⇔ −4 = 2 + 2. Thus the collection of all such points is a circular paraboloid with vertex at the origin, axis the -axis, which opens in the negative -direction. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.SECTION 12.6 CYLINDERS AND QUADRIC SURFACES ¤ 63 48. Let = ( ) be an arbitrary point whose distance from the -axis is twice its distance from the -plane. The distance from to the -axis is ( − )2 + 2 + 2 = 2 + 2 and the distance from to the -plane ( = 0) is || 1 = ||. Thus 2 + 2 = 2|| ⇔ 2 + 2 = 42 ⇔ 2 = (222) + (222). So the surface is a right circular cone with vertex the origin and axis the -axis. 49. (a) An equation for an ellipsoid centered at the origin with intercepts = ±, = ±, and = ± is 2 2 + 2 2 + 2 2 = 1. Here the poles of the model intersect the -axis at = ±6356523 and the equator intersects the - and -axes at = ±6378137, = ±6378137, so an equation is 2 (6378137)2 + 2 (6378137)2 + 2 (6356523)2 = 1 (b) Traces in = are the circles 2 (6378137)2 + 2 (6378137)2 = 1 − (63562523)2 ⇔ 2 + 2 = (6378137)2 − 6378 6356 137 5232 2. (c) To identify the traces in = we substitute = into the equation of the ellipsoid: 2 (6378137)2 + ()2 (6378137)2 + 2 (6356523)2 = 1 (1 + 2)2 (6378137)2 + 2 (6356523)2 = 1 2 (6378137)2(1 + 2) + 2 (6356523)2 = 1 As expected, this is a family of ellipses. 50. If we position the hyperboloid on coordinate axes so that it is centered at the origin with axis the -axis then its equation is given by 2 2 + 2 2 − 2 2 = 1. Horizontal traces in = are 22 + 22 = 1 + 22 , a family of ellipses, but we know that the traces are circles so we must have = . The trace in = 0 is 2 2 + 2 2 = 1 ⇔ 2 + 2 = 2 and since the minimum radius of 100 m occurs there, we must have = 100. The base of the tower is the trace in = −500 given by 2 2 + 2 2 = 1 + (−500) 2 2 but = 100 so the trace is 2 + 2 = 1002 + 50,0002 12 . We know the base is a circle of radius 140, so we must have 1002 + 50,0002 1 2 = 1402 ⇒ 2 = 140 502,−000 100 2 2 = 7813,250 and an equation for the tower is 2 1002 + 2 1002 − 2 (781,250)3 = 1 or 10,000 2 + 10,000 2 − 781 3,250 2 = 1, −500 ≤ ≤ 500. 51. If ( ) satisfies = 2 − 2, then = 2 − 2. 1: = + , = + , = + 2( − ), 2: = + , = − , = − 2( + ). Substitute the parametric equations of 1 into the equation of the hyperbolic paraboloid in order to find the points of intersection: = 2 − 2 ⇒ + 2( − ) = ( + )2 − ( + )2 = 2 − 2 + 2( − ) ⇒ = 2 − 2. As this is true for all values of , °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.64 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 1 lies on = 2 − 2. Performing similar operations with 2 gives: = 2 − 2 ⇒ − 2( + ) = ( − )2 − ( + )2 = 2 − 2 − 2( + ) ⇒ = 2 − 2. This tells us that all of 2 also lies on = 2 − 2. 52. Any point on the curve of intersection must satisfy both 22 + 42 − 22 + 6 = 2 and 22 + 42 − 22 − 5 = 0. Subtracting, we get 6 + 5 = 2, which is linear and therefore the equation of a plane. Thus the curve of intersection lies in this plane. 53. The curve of intersection looks like a bent ellipse. The projection of this curve onto the -plane is the set of points ( 0) which satisfy 2 + 2 = 1 − 2 ⇔ 2 + 22 = 1 ⇔ 2 + 2 1√22 = 1. This is an equation of an ellipse. 12 Review 1. This is false, as the dot product of two vectors is a scalar, not a vector. 2. False. For example, if u = i and v = −i then |u + v| = |0| = 0 but |u| + |v| = 1 + 1 = 2. 3. False. For example, if u = i and v = j then |u · v| = |0| = 0 but |u| |v| = 1 · 1 = 1. In fact, by Theorem 12.3.3, |u · v| = |u| |v|cos . 4. False. For example, |i × i| = |0| = 0 (see Example 12.4.2) but |i| |i| = 1 · 1 = 1. In fact, by Theorem 12.4.9, |u × v| = |u| |v|sin. 5. True, by Theorem 12.3.2, property 2. 6. False. Property 1 of Theorem 12.4.11 says that u × v = −v × u. 7. True. If is the angle between u and v, then by Theorem 12.4.9, |u × v| = |u| |v|sin = |v| |u|sin = |v × u|. (Or, by Theorem 12.4.11, |u × v| = |−v × u| = |−1| |v × u| = |v × u|.) 8. This is true by Theorem 12.3.2, property 4. 9. Theorem 12.4.11, property 2 tells us that this is true. 10. This is true by Theorem 12.4.11, property 4. 11. This is true by Theorem 12.4.11, property 5. 12. In general, this assertion is false; a counterexample is i × (i × j) 6= (i × i) × j. (See the paragraph preceding Theorem 12.4.11.) 13. This is true because u × v is orthogonal to u (see Theorem 12.4.8), and the dot product of two orthogonal vectors is 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 12 REVIEW ¤ 65 14. (u + v) × v = u × v + v × v [by Theorem 12.4.11, property 4] = u × v + 0 [by Example 12.4.2] = u × v, so this is true. 15. This is false. A normal vector to the plane is n = h6 −24i. Because h3 −12i = 1 2n, the vector is parallel to n and hence perpendicular to the plane. 16. This is false, because according to Equation 12.5.8, + + + = 0 is the general equation of a plane. 17. This is false. In R2, 2 + 2 = 1 represents a circle, but ( ) | 2 + 2 = 1 represents a three-dimensional surface, namely, a circular cylinder with axis the -axis. 18. This is false. In R3 the graph of = 2 is a parabolic cylinder (see Example 12.6.1). A paraboloid has an equation such as = 2 + 2. 19. False. For example, i · j = 0 but i 6= 0 and j 6= 0. 20. This is false. By Corollary 12.4.10, u × v = 0 for any nonzero parallel vectors u, v. For instance, i × i = 0. 21. This is true. If u and v are both nonzero, then by (7) in Section 12.3, u · v = 0 implies that u and v are orthogonal. But u × v = 0 implies that u and v are parallel (see Corollary 12.4.10). Two nonzero vectors can’t be both parallel and orthogonal, so at least one of u, v must be 0. 22. This is true. We know u · v = |u| |v| cos where |u| ≥ 0, |v| ≥ 0, and |cos| ≤ 1, so |u · v| = |u| |v| |cos| ≤ |u| |v|. 1. (a) The radius of the sphere is the distance between the points (−12 1) and (6 −23), namely, [6 − (−1)]2 + (−2 − 2)2 + (3 − 1)2 = √69. By the formula for an equation of a sphere (see page 835 [ET 795]), an equation of the sphere with center (−1 2 1) and radius √69 is ( + 1)2 + ( − 2)2 + ( − 1)2 = 69. (b) The intersection of this sphere with the -plane is the set of points on the sphere whose -coordinate is 0. Putting = 0 into the equation, we have ( − 2)2 + ( − 1)2 = 68 = 0 which represents a circle in the -plane with center (021) and radius √68. (c) Completing squares gives ( − 4)2 + ( + 1)2 + ( + 3)2 = −1 + 16 + 1 + 9 = 25. Thus the sphere is centered at (4 −1 −3) and has radius 5. 2. (a) (b) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.66 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE (c) (d) 3. u · v = |u| |v| cos45◦ = (2)(3) √22 = 3√2. |u × v| = |u| |v| sin 45◦ = (2)(3) √22 = 3√2. By the right-hand rule, u × v is directed out of the page. 4. (a) 2a + 3b = 2i + 2j − 4k + 9i − 6j + 3k = 11i − 4j − k (b) |b| = √9 + 4 + 1 = √14 (c) a · b = (1)(3) + (1)(−2) + (−2)(1) = −1 (d) a × b = i j k 1 1 −2 3 −2 1 = (1 − 4)i − (1 + 6)j + (−2 − 3)k = −3i − 7j − 5k (e) b × c = i j k 3 −2 1 0 1 −5 = 9i + 15j + 3k, |b × c| = 3√9 + 25 + 1 = 3√35 (f ) a · (b × c) = 1 1 −2 3 −2 1 0 1 −5 = −2 1 1 −5 − 3 1 0 −5 − 2 3 −2 0 1 = 9 + 15 − 6 = 18 (g) c × c = 0 for any c. (h) From part (e), a × (b × c) = a × (9i + 15j + 3k) = i j k 1 1 −2 9 15 3 = (3 + 30)i − (3 + 18)j + (15 − 9)k = 33i − 21j + 6k (i) The scalar projection is compa b = |b|cos = a · b |a| = − √16. (j) The vector projection is proja b = −√16|aa| = − 1 6(i + j − 2k). (k) cos = a · b |a| |b| = −1 √6√14 = −1 2√21 and = cos−12−√121 ≈ 96◦. 5. For the two vectors to be orthogonal, we need h3 2 i · h24 i = 0 ⇔ (3)(2) + (2)(4) + ()() = 0 ⇔ 2 + 6 + 8 = 0 ⇔ ( + 2)( + 4) = 0 ⇔ = −2 or = −4. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 12 REVIEW ¤ 67 6. We know that the cross product of two vectors is orthogonal to both given vectors. So we calculate (j + 2k) × (i − 2j + 3k) = [3 − (−4)]i − (0 − 2)j + (0 − 1)k = 7i + 2j − k. Then two unit vectors orthogonal to both given vectors are ±772i+ 2 + 22 j+ ( −−k1)2 = ±3√1 6 (7i + 2j − k), that is, 7 3 √6 i + 3 √2 6 j − 3 √1 6 k and − 3 √7 6 i − 3 √2 6 j + 3 √1 6 k. 7. (a) (u × v) · w = u · (v × w) = 2 (b) u · (w × v) = u · [−(v × w)] = −u · (v × w) = −2 (c) v · (u × w) = (v × u) · w = −(u × v) · w = −2 (d) (u × v) · v = u · (v × v) = u · 0 = 0 8. (a × b) · [(b × c) × (c × a)] = (a × b) · ([(b × c) · a]c − [(b × c) · c]a) [by Property 6 of the cross product] = (a × b) · [(b × c) · a]c = [a · (b × c)] (a × b) · c = [a · (b × c)] [a · (b × c)] = [a · (b × c)]2 9. For simplicity, consider a unit cube positioned with its back left corner at the origin. Vector representations of the diagonals joining the points (000) to (111) and (100) to (011) are h111i and h−111i. Let be the angle between these two vectors. h111i · h−1 11i = −1 + 1 + 1 = 1 = |h11 1i| |h−111i|cos = 3 cos ⇒ cos = 1 3 ⇒ = cos−1 1 3 ≈ 71◦. 10. −→ = h13 −1i, −→ = h−213i and −−→ = h−1 31i. By Equation 12.4.13, −→ · −→ × −−→ = 1 3 −1 −2 1 3 −1 3 1 = 1 3 3 1 − 3 −2 3 −1 1 − −2 1 −1 3 = −8 − 3 + 5 = −6. The volume is −→ · −→ × −−→ = 6 cubic units. 11. −→ = h10 −1i, −→ = h043i, so (a) a vector perpendicular to the plane is −→ × −→ = h0 + 4 −(3 + 0) 4 − 0i = h4 −34i. (b) 1 2 −→ × −→ = 1 2√16 + 9 + 16 = √241. 12. D = 4i + 3j + 6k, = F · D = 12 + 15 + 60 = 87 J 13. Let 1 be the magnitude of the force directed 20◦ away from the direction of shore, and let 2 be the magnitude of the other force. Separating these forces into components parallel to the direction of the resultant force and perpendicular to it gives 1 cos 20◦ + 2 cos 30◦ = 255 (1), and 1 sin 20◦ − 2 sin 30◦ = 0 ⇒ 1 = 2 sin 30◦ sin 20◦ (2). Substituting (2) into (1) gives 2(sin 30◦ cot 20◦ + cos 30◦) = 255 ⇒ 2 ≈ 114 N. Substituting this into (2) gives 1 ≈ 166 N. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.68 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 14. || = |r| |F|sin = (040)(50) sin(90◦ − 30◦) ≈ 173 N·m. 15. The line has direction v = h−323i. Letting 0 = (4 −12), parametric equations are = 4 − 3, = −1 + 2, = 2 + 3. 16. A direction vector for the line is v = h321i, so parametric equations for the line are = 1 + 3, = 2, = −1 + . 17. A direction vector for the line is a normal vector for the plane, n = h2 −1 5i, and parametric equations for the line are = −2 + 2, = 2 − , = 4 + 5. 18. Since the two planes are parallel, they will have the same normal vectors. Then we can take n = h14 −3i and an equation of the plane is 1( − 2) + 4( − 1) − 3( − 0) = 0 or + 4 − 3 = 6. 19. Here the vectors a = h4 − 3 0 − (−1) 2 − 1i = h111i and b = h6 − 33 − (−1) 1 − 1i = h340i lie in the plane, so n = a × b = h−4 3 1i is a normal vector to the plane and an equation of the plane is −4( − 3) + 3( − (−1)) + 1( − 1) = 0 or −4 + 3 + = −14. 20. If we first find two nonparallel vectors in the plane, their cross product will be a normal vector to the plane. Since the given line lies in the plane, its direction vector a = h2 −1 3i is one vector in the plane. We can verify that the given point (12 −2) does not lie on this line. The point (0 3 1) is on the line (obtained by putting = 0) and hence in the plane, so the vector b = h0 − 1 3 − 21 − (−2)i = h−113i lies in the plane, and a normal vector is n = a × b = h−6 −91i. Thus an equation of the plane is −6( − 1) − 9( − 2) + ( + 2) = 0 or 6 + 9 − = 26. 21. Substitution of the parametric equations into the equation of the plane gives 2 − + = 2(2 − ) − (1 + 3) + 4 = 2 ⇒ − + 3 = 2 ⇒ = 1. When = 1, the parametric equations give = 2 − 1 = 1, = 1 + 3 = 4 and = 4. Therefore, the point of intersection is (144). 22. Use the formula proven in Exercise 12.4.45(a). In the notation used in that exercise, a is just the direction of the line; that is, a = h1 −12i. A point on the line is (12 −1) (setting = 0), and therefore b = h1 − 02 − 0 −1 − 0i = h1 2 −1i. Hence = |a × b| |a| = |h1 −12i × h12 −1i| √1 + 1 + 4 = |h−3 3 3i| √6 = 27 6 = √32. 23. Since the direction vectors h2 34i and h6 −12i aren’t parallel, neither are the lines. For the lines to intersect, the three equations 1 + 2 = −1 + 6, 2 + 3 = 3 − , 3 + 4 = −5 + 2 must be satisfied simultaneously. Solving the first two equations gives = 1 5, = 2 5 and checking we see these values don’t satisfy the third equation. Thus the lines aren’t parallel and they don’t intersect, so they must be skew. 24. (a) The normal vectors are h11 −1i and h2 −34i. Since these vectors aren’t parallel, neither are the planes parallel. Also h1 1 −1i · h2 −34i = 2 − 3 − 4 = −5 6= 0 so the normal vectors, and thus the planes, are not perpendicular. (b) cos = h11 −√13i · h √29 2 −34i = −√587 and = cos−1− √587 ≈ 122◦ [or we can say ≈ 58◦]. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 12 REVIEW ¤ 69 25. n1 = h10 −1i and n2 = h012i. Setting = 0, it is easy to see that (130) is a point on the line of intersection of − = 1 and + 2 = 3. The direction of this line is v1 = n1 × n2 = h1 −21i. A second vector parallel to the desired plane is v2 = h1 1 −2i, since it is perpendicular to + − 2 = 1. Therefore, the normal of the plane in question is n = v1 × v2 = h4 − 11 + 2 1 + 2i = 3h1 1 1i. Taking (0 0 0) = (130), the equation we are looking for is ( − 1) + ( − 3) + = 0 ⇔ + + = 4. 26. (a) The vectors −→ = h−1 − 2 −1 − 110 − 1i = h−3 −29i and −→ = h1 − 23 − 1 −4 − 1i = h−12 −5i lie in the plane, so n = −→ × −→ = h−3 −29i × h−1 2 −5i = h−8 −24 −8i or equivalently h131i is a normal vector to the plane. The point (211) lies on the plane so an equation of the plane is 1( − 2) + 3( − 1) + 1( − 1) = 0 or + 3 + = 6. (b) The line is perpendicular to the plane so it is parallel to a normal vector for the plane, namely h1 3 1i. If the line passes through (−1 −110) then symmetric equations are − (−1) 1 = − (−1) 3 = − 10 1 or + 1 = + 1 3 = − 10. (c) Normal vectors for the two planes are n1 = h131i and n2 = h2 −4 −3i. The angle between the planes is given by cos = n1 · n2 |n1| |n2| = h1 3 1i · h2 −4 −3i √12 + 32 + 12 22 + (−4)2 + (−3)2 = 2 − 12 − 3 √11√29 = − 13 √319 Thus = cos−1−√13 319 ≈ 137◦ or 180◦ − 137◦ = 43◦. (d) From part (c), the point (204) lies on the second plane, but notice that the point also satisfies the equation of the first plane, so the point lies on the line of intersection of the planes. A vector v in the direction of this intersecting line is perpendicular to the normal vectors of both planes, so take v = n1 × n2 = h131i × h2 −4 −3i = h−55 −10i or equivalently we can take v = h1 −12i. Parametric equations for the line are = 2 + , = −, = 4 + 2. 27. By Exercise 12.5.75, = 3|−2 2+ 1 −2(−+ ( 24) −|4)2 = √22 26. 28. The equation = 3 represents a plane parallel to the -plane and 3 units in front of it. 29. The equation = represents a plane perpendicular to the -plane and intersecting the -plane in the line = , = 0. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.70 ¤ CHAPTER 12 VECTORS AND THE GEOMETRY OF SPACE 30. The equation = 2 represents a parabolic cylinder whose trace in the -plane is the -axis and which opens to the right. 31. The equation 2 = 2 + 42 represents a (right elliptical) cone with vertex at the origin and axis the -axis. 32. 4 − + 2 = 4 is a plane with intercepts (100), (0 −40), and (0 0 2). 33. An equivalent equation is −2 + 2 4 − 2 = 1, a hyperboloid of two sheets with axis the -axis. For || 2, traces parallel to the -plane are circles. 34. An equivalent equation is −2 + 2 + 2 = 1, a hyperboloid of one sheet with axis the -axis. 35. Completing the square in gives 42 + 4( − 1)2 + 2 = 4 or 2 + ( − 1)2 + 2 4 = 1, an ellipsoid centered at (010). 36. Completing the square in and gives = ( − 1)2 + ( − 2)2, a circular paraboloid with vertex (012) and axis the horizontal line = 1, = 2. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 12 REVIEW ¤ 71 37. 42 + 2 = 16 ⇔ 2 4 + 2 16 = 1. The equation of the ellipsoid is 2 4 + 2 16 + 2 2 = 1, since the horizontal trace in the plane = 0 must be the original ellipse. The traces of the ellipsoid in the -plane must be circles since the surface is obtained by rotation about the -axis. Therefore, 2 = 16 and the equation of the ellipsoid is 2 4 + 2 16 + 2 16 = 1 ⇔ 42 + 2 + 2 = 16. 38. The distance from a point ( ) to the plane = 1 is | − 1|, so the given condition becomes | − 1| = 2( − 0)2 + ( + 1)2 + ( − 0)2 ⇒ | − 1| = 22 + ( + 1)2 + 2 ⇒ ( − 1)2 = 42 + 4( + 1)2 + 42 ⇔ −3 = 42 + (32 + 10) + 42 ⇔ 16 3 = 42 + 3 + 5 32 + 42 ⇒ 3 42 + 16 9 + 5 32 + 3 42 = 1. This is the equation of an ellipsoid whose center is 0 − 5 30. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.PROBLEMS PLUS 1. Since three-dimensional situations are often difficult to visualize and work with, let us first try to find an analogous problem in two dimensions. The analogue of a cube is a square and the analogue of a sphere is a circle. Thus a similar problem in two dimensions is the following: if five circles with the same radius are contained in a square of side 1 m so that the circles touch each other and four of the circles touch two sides of the square, find . The diagonal of the square is √2. The diagonal is also 4 + 2. But is the diagonal of a smaller square of side . Therefore = √2 ⇒ √2 = 4 + 2 = 4 + 2√2 = 4 + 2√2 ⇒ = 4 + 2 √2√2. Let’s use these ideas to solve the original three-dimensional problem. The diagonal of the cube is √12 + 12 + 12 = √3. The diagonal of the cube is also 4 + 2 where is the diagonal of a smaller cube with edge . Therefore = √2 + 2 + 2 = √3 ⇒ √3 = 4 + 2 = 4 + 2√3 = 4 + 2√3. Thus = √3 4 + 2√3 = 2√3 − 3 2 . The radius of each ball is √3 − 3 2 m. 2. Try an analogous problem in two dimensions. Consider a rectangle with length and width and find the area of in terms of and . Since contains , it has area () = + the area of two × 1 rectangles + the area of two 1 × rectangles + the area of four quarter-circles of radius 1 as seen in the diagram. So () = + 2 + 2 + · 12. Now in three dimensions, the volume of is + 2( × × 1) + 2(1 × × ) + 2( × 1 × ) + the volume of 4 quarter-cylinders with radius 1 and height + the volume of 4 quarter-cylinders with radius 1 and height + the volume of 4 quarter-cylinders with radius 1 and height + the volume of 8 eighths of a sphere of radius 1 So () = + 2 + 2 + 2 + · 12 · + · 12 · + · 12 · + 4 3 · 13 = + 2( + + ) + ( + + ) + 4 3 °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. 73 NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.74 ¤ CHAPTER 12 PROBLEMS PLUS 3. (a) We find the line of intersection as in Example 12.5.7(b). Observe that the point (−1 ) lies on both planes. Now since lies in both planes, it is perpendicular to both of the normal vectors n1 and n2, and thus parallel to their cross product n1 × n2 = i j k 1 1 1 − = 2 −2 + 1 −2 − 1 So symmetric equations of can be written as + 1 −2 = − 2 − 1 = − 2 + 1, provided that 6= 0, ±1. If = 0, then the two planes are given by + = 0 and = −1, so symmetric equations of are = −1, = −. If = −1, then the two planes are given by − + + = −1 and + + = −1, and they intersect in the line = 0, = − − 1. If = 1, then the two planes are given by + + = 1 and − + = 1, and they intersect in the line = 0, = 1 − . (b) If we set = in the symmetric equations and solve for and separately, we get + 1 = ( − )(−2) 2 + 1 , − = ( − )(2 − 1) 2 + 1 ⇒ = −2 + (2 − 1) 2 + 1 , = (2 − 1) + 2 2 + 1 . Eliminating from these equations, we have 2 + 2 = 2 + 1. So the curve traced out by in the plane = is a circle with center at (00 ) and radius √2 + 1. (c) The area of a horizontal cross-section of the solid is () = (2 + 1), so = 01 () = 1 33 + 1 0 = 43 . 4. (a) We consider velocity vectors for the plane and the wind. Let v be the initial, intended velocity for the plane and v the actual velocity relative to the ground. If w is the velocity of the wind, v is the resultant, that is, the vector sum v + w as shown in the figure. We know v = 180j, and since the plane actually flew 80 km in 1 2 hour, |v| = 160. Thus v = (160 cos 85◦)i + (160 sin 85◦)j ≈ 139i + 1594j. Finally, v + w = v, so w = v − v ≈ 139i − 206j. Thus, the wind velocity is about 139i − 206j, and the wind speed is |w| ≈ (139)2 + (−206)2 ≈ 249 kmh. (b) Let v be the velocity the pilot should have taken. The pilot would need to head a little west of north to compensate for the wind, so let be the angle v makes with the north direction. Then we can write v = h180 cos( + 90◦)180 sin( + 90◦)i. With the effect of the wind, the actual velocity (with respect to the ground) will be v + w, which we want to be due north. Equating horizontal components of the vectors, we must have 180 cos( + 90◦) + 160 cos 85◦ = 0 ⇒ cos( + 90◦) = − 160 180 cos 85◦ ≈ −00775, so ≈ cos−1(−00775) − 90◦ ≈ 44◦. Thus the pilot should have headed about 44◦ west of north. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 12 PROBLEMS PLUS ¤ 75 5. v3 =projv1v2 = v1 · v2 |v1|2 v1 = 5 22 v1 so |v3| = 5 22 |v1| = 52, v4 =projv2v3 = v2 · v3 |v2|2 v2 = v2 · 5 22 v1 |v2|2 v2 = 5 22 · 32 (v1 · v2)v2 = 225·232 v2 ⇒ |v4| = 225·232 |v2| = 2252· 3, v5 =projv3v4 = v3 · v4 |v3|2 v3 = 5 22 v1 · 225232 v2 5 2 2 252 v1 = 245·232 (v1 · v2) v1 = 245·332 v1 ⇒ |v5| = 53 24 · 32 |v1| = 235·332 . Similarly, |v6| = 245·433 , |v7| = 255·534 , and in general, |v| = 2−52·−32−3 = 3 5 6 −2. Thus ∞ =1 |v| = |v1| + |v2| + ∞ =3 3 5 6 −2 = 2 + 3 + ∞ =1 3 5 6 = 5 + ∞ =1 5 2 5 6 −1 = 5 + 5 2 1 − 5 6 [sum of a geometric series] = 5 + 15 = 20 6. Completing squares in the inequality 2 + 2 + 2 136 + 2( + 2 + 3) gives ( − 1)2 + ( − 2)2 + ( − 3)2 150 which describes the set of all points ( ) whose distance from the point (1 2 3) is less than √150 = 5√6. The distance from to (−114) is √4 + 1 + 1 = √6, so the largest possible sphere that passes through and satisfies the stated conditions extends 5√6 units in the opposite direction, giving a diameter of 6√6. (See the figure.) Thus the radius of the desired sphere is 3√6, and its center is 3√6 units from in the direction of . A unit vector in this direction is u = √16 h2 1 −1i, so starting at (−114) and following the vector 3√6u = h63 −3i we arrive at the center of the sphere, (541). An equation of the sphere then is ( − 5)2 + ( − 4)2 + ( − 1)2 = 3√62 or ( − 5)2 + ( − 4)2 + ( − 1)2 = 54. 7. (a) When = , the block is not moving, so the sum of the forces on the block must be 0, thus N + F + W = 0 This relationship is illustrated geometrically in the figure. Since the vectors form a right triangle, we have tan() = |F| |N| = = . (b) We place the block at the origin and sketch the force vectors acting on the block, including the additional horizontal force H, with initial points at the origin. We then rotate this system so that F lies along the positive -axis and the inclined plane is parallel to the -axis. (See the following figure.) °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.76 ¤ CHAPTER 12 PROBLEMS PLUS |F| is maximal, so |F| = for . Then the vectors, in terms of components parallel and perpendicular to the inclined plane, are N = j F = ()i W = (− sin)i + (− cos)j H = (min cos)i + (−min sin)j Equating components, we have − sin + min cos = 0 ⇒ min cos + = sin − cos − min sin = 0 ⇒ min sin + cos = (1) (2) (c) Since (2) is solved for , we substitute into (1): min cos + (min sin + cos) = sin ⇒ min cos + min sin = sin − cos ⇒ min = sin cos−+cos sin = 1 + tan−tan From part (a) we know = tan, so this becomes min = 1 + tan tan −tan tan and using a trigonometric identity, this is tan( − ) as desired. Note for = , min = tan 0 = 0, which makes sense since the block is at rest for , thus no additional force H is necessary to prevent it from moving. As increases, the factor tan( − ), and hence the value of min, increases slowly for small values of − but much more rapidly as − becomes significant. This seems reasonable, as the steeper the inclined plane, the less the horizontal components of the various forces affect the movement of the block, so we would need a much larger magnitude of horizontal force to keep the block motionless. If we allow → 90◦, corresponding to the inclined plane being placed vertically, the value of min is quite large; this is to be expected, as it takes a great amount of horizontal force to keep an object from moving vertically. In fact, without friction (so = 0), we would have → 90◦ ⇒ min → ∞, and it would be impossible to keep the block from slipping. (d) Since max is the largest value of that keeps the block from slipping, the force of friction is keeping the block from moving up the inclined plane; thus, F is directed down the plane. Our system of forces is similar to that in part (b), then, except that we have F = −()i. (Note that |F| is again maximal.) Following our procedure in parts (b) and (c), we °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.CHAPTER 12 PROBLEMS PLUS ¤ 77 equate components: − − sin + max cos = 0 ⇒ max cos − = sin − cos − max sin = 0 ⇒ max sin + cos = Then substituting, max cos − (max sin + cos) = sin ⇒ max cos − max sin = sin + cos ⇒ max = sin cos+−cos sin = 1tan − +tan = 1tan − tan + tan tan = tan( + ) We would expect max to increase as increases, with similar behavior as we established for min, but with max values always larger than min. We can see that this is the case if we graph max as a function of , as the curve is the graph of min translated 2 to the left, so the equation does seem reasonable. Notice that the equation predicts max → ∞ as → (90◦ − ). In fact, as max increases, the normal force increases as well. When (90◦ − ) ≤ ≤ 90◦, the horizontal force is completely counteracted by the sum of the normal and frictional forces, so no part of the horizontal force contributes to moving the block up the plane no matter how large its magnitude. 8. (a) The largest possible solid is achieved by starting with a circular cylinder of diameter 1 with axis the -axis and with a height of 1. This is the largest solid that creates a square shadow with side length 1 in the -direction and a circular disk shadow in the -direction. For convenience, we place the base of the cylinder on the -plane so that it intersects the - and -axes at ± 1 2 . We then remove as little as possible from the solid that leaves an isosceles triangle shadow in the -direction. This is achieved by cutting the solid with planes parallel to the -axis that intersect the -axis at 1 and the -axis at ± 1 2 (see the figure). To compute the volume of this solid, we take vertical slices parallel to the -plane. The equation of the base of the solid is 2 + 2 = 1 4 , so a cross-section units to the right of the origin is a rectangle with base 2 1 4 − 2. For 0 ≤ ≤ 1 2 , the solid is cut off on top by the plane = 1 − 2, so the height of the rectangular cross-section is 1 − 2 and the cross-sectional area is () = 2 1 4 − 2 (1 − 2). The volume of the right half of the solid is 0122 1 4 − 2 (1 − 2) = 2012 1 4 − 2 − 4012 1 4 − 2 = 2 1 4 area of a circle of radius 1 2 − 4− 1 3 1 4 − 2321 02 = 2 1 4 · 1 22 + 4 30 − 1 432 = 8 − 1 6 Thus the volume of the solid is 2 8 − 1 6 = 4 − 1 3 ≈ 045. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved.78 ¤ CHAPTER 12 PROBLEMS PLUS (b) There is not a smallest volume. We can remove portions of the solid from part (a) to create smaller and smaller volumes as long as we leave the “skeleton” shown in the figure intact (which has no volume at all and is not a solid). Thus we can create solids with arbitrarily small volume. °c 2016 Cengage Learning. All Rights Reserved. May not be scanned, copied, or duplicated, or posted to a publicly accessible website, in whole or in part. NOT FOR SALE INSTRUCTOR USE ONLY © Cengage Learning. All Rights Reserved. [Show More]
Last updated: 1 year ago
Preview 1 out of 78 pages
Instant download
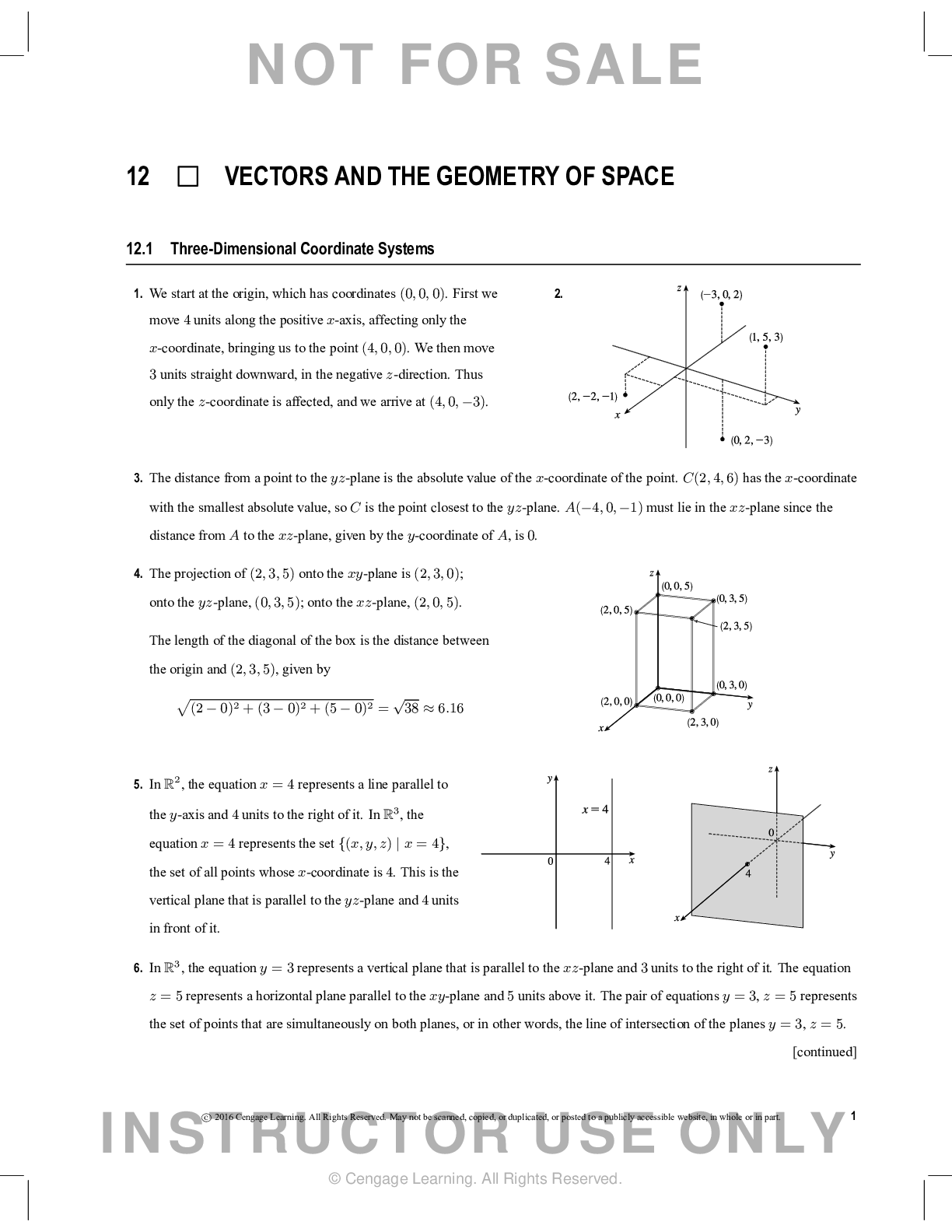
Buy this document to get the full access instantly
Instant Download Access after purchase
Add to cartInstant download
Reviews( 0 )
Document information
Connected school, study & course
About the document
Uploaded On
Jan 06, 2020
Number of pages
78
Written in
Additional information
This document has been written for:
Uploaded
Jan 06, 2020
Downloads
0
Views
161