Statistics > QUESTIONS & ANSWERS > Sophia Statistics Unit 3 Milestone. With RATIONALE and CONCEPT. Score 22/27 (All)
Sophia Statistics Unit 3 Milestone. With RATIONALE and CONCEPT. Score 22/27
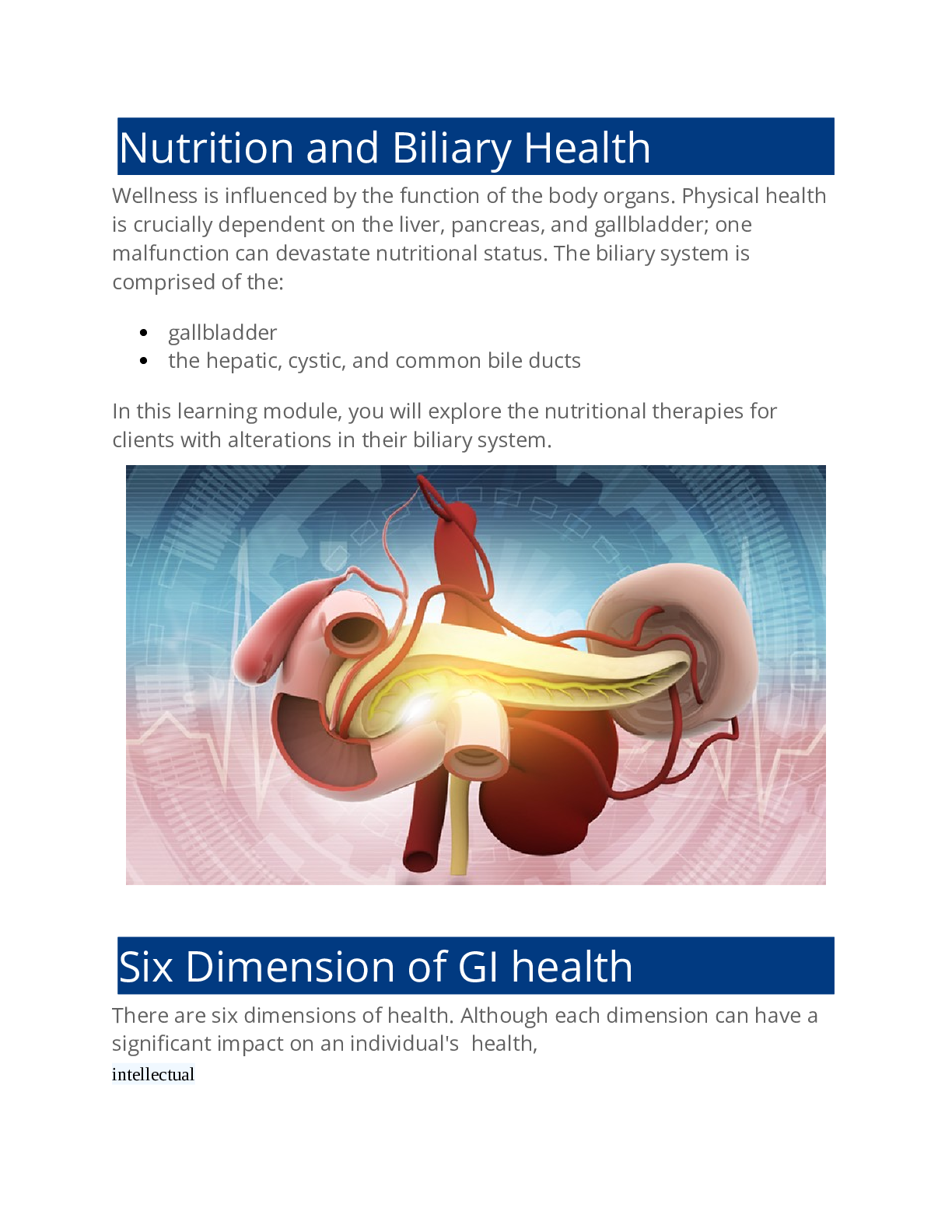
Document Content and Description Below
UNIT 3 — MILESTONE 3 Score 22/27 You passed this Milestone 22 questions were answered correctly. 5 questions were answered incorrectly. 1 Which of the following is a property of binomial distr... ibutions? The sum of the probabilities of successes and failures is always 1. All trials are dependent. The expected value is equal to the number of successes in the experiment. There are exactly three possible outcomes for each trial. Recall that for any probability distribution, the sum of all the probabilities must sum to 1. Binomial Distribution I need help with this question 2 Zhi and her friends moved on to the card tables at the casino. Zhi wanted to figure out the probability of drawing a face card or an Ace. Choose the correct probability of drawing a face card or an Ace. Answer choices are in the form of a percentage, rounded to the nearest whole number. 8% 4% 31% 25% Since the two events, drawing a face card and drawing an ace card, are non-overlapping, we can use the following formula: "Either/Or" Probability for Non-Overlapping Events I need help with this question 3 John is playing a game with a standard deck of playing cards. He wants to draw a jack on the first try. Which of the following statements is true? The probability that John draws a jack on the first try is 1/13. If John replaces the card, re-shuffles, and draws again, the probability that he will pull another jack increases. The probability that John draws a jack on the first try is 1/13. If John replaces the card, re-shuffles, and draws again, the probability that he will pull another jack stays the same. The probability that John draws a jack on the first try is 3/13. If John replaces the card, re-shuffles, and draws again, the probability that he will pull another jack stays the same. The probability that John draws a jack on the first try is 1/13. If John replaces the card, re-shuffles, and draws again, the probability that he will pull another jack decreases. Events are said to be independent if one event does not influence the likelihood of the other. Since John reshuffles the deck and puts the card back in the deck, the probability should be the same and the first draw will not influence the second. Independent vs. Dependent Events I need help with this question 4 A magician asks an audience member to pick any number from 6 to 15. What is the theoretical probability that an individual chooses the number the magician has in mind? If we suppose that the card chosen by the magician is fixed, then there are 10 possible values, {6, 7, 8, 9, 10, 11, 12, 13, 14, or 15}, that are all equally likely. So, the probability that a specific value is chosen is: Theoretical Probability/A Priori Method I need help with this question 5 Select the following statement that describes non-overlapping events. Receiving the Queen of Diamonds fulfills Luke's need of getting both a face card and a diamond. Luke wants a red card so he can have a winning hand, and he receives the five of clubs. Luke needs to roll an odd number to win. When it’s his turn, he rolls a five. To win, Luke needs a black card. He receives an eight of spades. Events are non-overlapping if the two events cannot both occur in a single trial of a chance experiment. Since he wants a red card {Ace, 2, 3, 4, 5, 6, 7, 8, 9, 10, Jack, Queen, or King: In either Diamond or Hearts} and he got the Five of Clubs, there is no overlap. Overlapping Events I need help with this question 6 Jake tosses a coin and rolls a six-sided die. All of the following are possible outcomes EXCEPT: Tails, Three Heads, Seven Heads, Five Tails, One Recall a coin has heads and tails and a standard die has six values, {1, 2, 3, 4, 5, or 6}. So, obtaining a value of 7 is not possible. Outcomes and Events I need help with this question 7 Asmita went to a blackjack table at the casino. At the table, the dealer has just shuffled a standard deck of 52 cards. Asmita has had good luck at blackjack in the past, and she actually got three blackjacks with Aces in a row the last time she played. Because of this lucky run, Asmita thinks that Ace is the luckiest card. The dealer deals the first card to her. In a split second, she can see that it is a non-face card, but she is unsure if it is an Ace. What is the probability of the card being an Ace, given that it is a non-face card? Answer choices are in a percentage format, rounded to the nearest whole number. 8% 77% 69% 10% The probability of it being an Ace given it is a Non-face card uses the conditional formula: Note, that in a standard deck of 52 cards, there are 12 face cards, so 40 non-face cards. Of those non-face cards, there are only 4 Aces. Conditional Probability I need help with this question 8 Patricia was having fun playing poker. She needed the next two cards dealt to be spades so she could make a flush (five cards of the same suit). There are 12 cards left in the deck, and three are spades. What is the probability that the two cards dealt to Patricia (without replacement) will both be spades? Answer choices are in percentage format, rounded to the nearest whole number. 17% 18% 5% 25% If there are 12 cards left in the deck with 3 spades, the probability of being dealt 2 spades if they are dealt without replacement means that we have dependent events because the outcome of the first card will affect the probability of the second card. We can use the following formula: The probability that the first card is a spade would be 3 out of 12, or . The probability that the second card is a spade, given that the first card was also a spade, would be because we now have only 11 cards remaining and only two of those cards are spades (since the first card was a spade). So we can use these probabilities to find the probability that the two cards will both be spades: "And" Probability for Dependent Events I need help with this question 9 David is playing a game where he flips two coins and counts the total number of heads. The possible outcomes and probabilities are shown in the probability distribution below. What is the expected value for the number of heads from flipping two coins? 1 2 3 1.5 The expected value, also called the mean of a probability distribution, is found by adding the products of each individual outcome and its probability. We can use the following formula to calculate the expected value, E(X): Expected Value I need help with this question 10 Using the Venn Diagram below, what is the conditional probability of event A occurring, assuming that event B has already occurred [P(A|B)]? 0.05 0.22 0.71 0.10 To get the probability of A given B has occurred, we can use the following conditional formula: The probability of A and B is the intersection, or overlap, of the Venn diagram, which is 0.1. The probability of B is all of Circle B, or 0.1 + 0.35 = 0.45. Conditional Probability I need help with this question 11 The average number of tunnel construction projects that take place at any one time in a certain state is 3. Find the probability of exactly five tunnel construction projects taking place in this state. 0.048 0.023 0.10 0.020 Since we are finding the probability of a given number of events happening in a fixed interval when the events occur independently and the average rate of occurrence is known, we can use the following Poisson distribution formula: P left parenthesis X equals k right parenthesis equals fraction numerator lambda to the power of k e to the power of negative lambda end exponent over denominator k factorial end fraction The variable k is the given number of occurrences, which in this case, is 5 projects. The variable λ is the average rate of event occurrences, which in this case, is 3 projects. Poisson Distribution I need help with this question 12 Peter randomly draws a card from a deck of 24. The odds in favor of his drawing a spade from the cards are 1:3. What is the probability ratio for Peter to draw a spade? Recall that we can go from " " odds to a probability by rewriting it as the fraction " ". So odds of 1:3 is equivalent to the following probability: Odds I need help with this question 13 Ryan is playing a multiplication game with a pile of 26 cards, each with a number on them. Each turn, he flips over two of the cards, and has to multiply the numbers. How many possible outcomes are there on Ryan's first turn flipping two cards? 676 650 26 52 We can use the general counting principle and note that for each step, we simply multiply all the possibilities at each step to get the total number of outcomes. If we assume that the numbers are 1 - 26, then the overall number of outcomes is: Note that once a number is chosen it cannot be chosen again. So the number of possible outcomes for the first card would be 26 since they could choose any card number 1 through 26. However, the second card chosen would only have 25 possible outcomes since the first card has already been drawn. Fundamental Counting Principle I need help with this question 14 A credit card company surveys 125 of their customers to ask about satisfaction with customer service. The results of the survey, divided by gender, are shown below. Males Females Extremely Satisfied 25 7 Satisfied 21 13 Neutral 13 16 Dissatisfied 9 14 Extremely Dissatisfied 2 5 If a survey is selected at random, what is the probability that the person is a female with neutral feelings about customer service? Answer choices are rounded to the hundredths place. 0.13 0.19 0.29 0.5 0.81 If we want the probability of selecting a survey that is from a female who marked "neutral feelings," we just need to look at the box that is associated with both categories, or 16. To calculate the probability, we can use the following formula: Two-Way Tables/Contingency Tables I need help with this question 15 Three hundred students in a school were asked to select their favorite fruit from a choice of apples, oranges, and mangoes. This table lists the results. Boys Girls Apple 66 46 Orange 52 41 Mango 40 55 If you were to choose a boy from the group, what is the probability that mangoes are his favorite fruit? Answer choices are rounded to the hundredths place. 0.25 0.13 0.39 0.75 The probability of a person picking mangoes as his favorite fruit given he is a boy is a conditional probability. We can use the following formula: Remember, to find the total number of boys, we need to add all values in this column: 66 + 52 + 40 = 158. Conditional Probability and Contingency Tables I need help with this question 16 What is the probability of drawing a red card or a queen from a standard deck of 52 cards? Since it is possible for a card to be both red and a queen, these two events are overlapping. We can use the following formula: In a standard deck of cards, half of the 52 cards are red, so . There is a total of 4 Queens, so . Of the 4 queens, 2 are red and 2 are black, so . "Either/Or" Probability for Overlapping Events I need help with this question 17 Using this Venn diagram, what is the probability that event A or event B occurs? 0.60 0.78 0.42 0.22 To find the probability that event A or event B occurs, we can use the following formula for overlapping events: The probability of event A is ALL of circle A, or 0.39 + 0.18 = 0.57. The probability of event B is ALL of circle B, or 0.21 + 0.18 = 0.39. The probability of event A and B is the intersection of the Venn diagram, or 0.18. We can also simply add up all the parts = 0.39 + 0.18 + 0.21 = 0.78. "Either/Or" Probability for Overlapping Events I need help with this question 18 Phil is randomly drawing cards from a deck of 52. He first draws a Queen, places it back in the deck, shuffles the deck, and then draws another card. What is the probability of drawing a Queen, placing it back in the deck, and drawing any face card? Answer choices are in the form of a percentage, rounded to the nearest whole number. 31% 2% 25% 7% Since Phil puts the card back and re-shuffles, the two events (first draw and second draw) are independent of each other. To find the probability of getting a Queen on the first draw and a face card on the second draw, we can use the following formula: Note that the probability of drawing a Queen card is , while the probability of drawing a face card is . "And" Probability for Independent Events I need help with this question 19 Which of the following situations describes a continuous distribution? A probability distribution showing the amount of births in a hospital in a month A probability distribution showing the number of vaccines given to babies during their first year of life A probability distribution showing the weights of newborns A probability distribution showing the average number of days mothers spent in the hospital Since the weight of newborns can be an infinite number of values, such as 8 pounds, 9 ounces, etc, this would be an example of a continuous distribution. Probability Distribution I need help with this question 20 Which of the following is an example of a false negative? Test results confirm that a woman is not pregnant. Test results confirm that a woman is pregnant. Test results indicate that a woman is not pregnant when she is. Test results indicate that a woman is pregnant when she is not. Since the test results indicate negatively, showing that the woman is not pregnant when in fact she is pregnant, this is a false negative. False Positives/False Negatives I need help with this question 21 Mark looked at the statistics for his favorite baseball player, Jose Bautista. Mark looked at seasons when Bautista played 100 or more games and found that Bautista's probability of hitting a home run in a game is 0.173. If Mark uses the normal approximation of the binomial distribution, what will be the variance of the number of home runs Bautista is projected to hit in 100 games? Answer choices are rounded to the tenths place. 14.3 17.3 3.8 0.8 In this situation, we know: n = sample size = 100 p = success probability = 0.173 We can also say that q, or the complement of p, equals: q = 1 - p = 1 - 0.173 = 0.827 The variance is equivalent to n*p*q: Normal Distribution Approximation of the Binomial Distribution I need help with this question 22 A basketball player makes 80% of his free throws. We set him on the free throw line and told him to shoot free throws until he misses. Let the random variable X be the number of free throws taken by the player until he misses. Assuming that his shots are independent, what is the probability of this player missing a free throw for the first time on the fifth attempt? 0.0016 0.00128 0.4096 0.08192 Since we are looking for the probability until the first success, we will use the following Geometric distribution formula: P left parenthesis X equals k right parenthesis equals left parenthesis 1 minus p right parenthesis to the power of k minus 1 end exponent p The variable k is the number of trials until the first success, which in this case, is 5 attempts. The variable p is the probability of success, which in this case, a success is considered missing a free throw. If the basketball player has an 80% of making it, he has a 20%, or 0.20, chance of missing. Geometric Distribution I need help with this question 23 Sarah throws a fair die multiple times, recording the total number of "2"s she throws and then calculating the proportion of "2"s she has thrown so far after each throw. She then constructs a graph to visualize her results. Which of the following statements is FALSE? The theoretical probability of getting a 2 is 0.167 for each throw. This is an example of the law of large numbers. The relative frequency of "2"s thrown changes as Sarah throws the die more. The probability distribution for the possible number of outcomes changes as the total number of throws increases. The probability distribution for the outcomes doesn't change; however, the sampling distribution for the outcomes does. Law of Large Numbers/Law of Averages I need help with this question 24 Two sets A and B are shown in the Venn diagram below. Which statement is TRUE? Sets A and B have 3 common elements. Set A has 8 elements. Set B has 7 elements. There are a total of 2 elements shown in the Venn diagram. The intersection, or middle section, would show the common elements, which is 3. The number of elements of Set A is everything in Circle A, or 8+3 = 11 elements, not 8 elements. The number of elements of Set B is everything in Circle B, or 7+3 = 10 elements, not 7 elements. To get the total number of items in the Venn diagram, we add up what is in A and B and outside, which is 8+3+7+2=20 elements, not 2 elements. Venn Diagrams I need help with this question 25 Kyle was trying to decide which type of soda to restock based on popularity: regular cola or diet cola. After studying the data, he noticed that he sold less diet cola on weekdays and weekends. However, after combing through his entire sales records, he actually sold more diet cola than regular cola. Which paradox had Kyle encountered? False Negative False Positive Simpson's Paradox Benford's Law This is an example of Simpson's paradox, which is when the trend overall is not the same that is examined in smaller groups. Since the sale of diet coke overall is larger but this trend changes when looking at weekend/weekday, this is a reversal of the trend. Paradoxes I need help with this question 26 Maria flipped a coin 60 times, and the coin came up tails 32 times. What is the relative frequency of the coin turning up heads in this experiment? Answer choices are rounded to the hundredths place. 0.47 0.53 1.88 2.14 Recall that, of the 60 flips, there are 32 tails. This means the remaining are heads, or 60-32 = 28 heads. The relative frequency of a head is: Relative Frequency Probability/Empirical Method I need help with this question 27 What is the probability of NOT rolling a four when rolling a six sided die? Recall that the probability of a complement, or the probability of something NOT happening, can be calculated by finding the probability of that event happening, and then subtracting from 1. Note that the probability of rolling a four would be 1/6. So the probability of NOT rolling a four is equivalent to: Complement of an Event I need help with this question © 2020 SOPHIA Learning, LLC. SOPHIA is a registered trademark of SOPHIA Learning, LLC. About Contact Us Privacy Policy Terms of Use [Show More]
Last updated: 1 year ago
Preview 1 out of 22 pages

Reviews( 2 )

by anitra mcknight · 3 years ago
Thank you for the review. by QuizMaster. 3 years ago

by QuizMaster · 3 years ago
Document information
Connected school, study & course
About the document
Uploaded On
Oct 15, 2020
Number of pages
22
Written in
Additional information
This document has been written for:
Uploaded
Oct 15, 2020
Downloads
1
Views
509












.png)








.png)

.png)




.png)
.png)

.png)





